
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Применение распределения Пуассона для оценки риска аварий
|
|
Оценка степени риска поражения людей и нанесения ущерба при авариях связана с задачей прогнозирования показателей надежности и остаточного ресурса функционирующей системы. Наиболее важным вопросом является установление допустимых сроков дальнейшей эксплуатации индивидуального объекта при конкретном значении риска аварии. Ответственность за соответствующие инженерные решения о мерах по снижению риска или о приостановке функционирования объекта лежит на комиссии, в состав которой должны входить специалисты-эксперты и представители административных органов.
Одним из основных показателей надежности объекта является вероятность P(t) безотказной работы на некотором временном интервале или функция надежности. Функция Q(t)= 1- P(t), дополняющая P(t) до единицы и характеризующая вероятность отказа, является функцией риска аварии — поражения людей и нанесения материального ущерба.
Для оценки риска применяют некоторые модели теории надежности. Среди них модели высоконадежных систем, для которых аварийные ситуации представляют редкие события, а также модели стареющих систем, качество которых в процессе эксплуатации ухудшается вследствие ползучести, различных видов усталости, износа и других видов повреждений.
Прогнозирование аварийных ситуаций возможно на основе элементарной статистики и дискретного распределения Пуассона, часто применяемого к редким событиям и природным явлениям.
Функцией риска аварии из-за отказа нормального функционирования объекта называют вероятность отказа:
H(t)= 1- P(t), P (t) = exp (- ∫ λ (ξ) d ξ) (8.18)
λ (t) = - P’ (t) / P (t),
где Р(t) – вероятность безотказной работы (функция надежности), λ(t) – интенсивность отказов, равная вероятности того, что после безотказной работы до момента времени t авария произойдет в последующем малом отрезке времени.
Опыт показывает, что после небольшого начального периода эксплуатации (приработки) функция λ(t) длительный период достаточно стабильна, т.е. λ(t)= const. Влияние интенсивного старения за счет коррозионного износа, усталости и других факторов должно исключаться регламентированием допустимого срока службы.
Принимая для периода нормального (спокойного) функционирования
λ(t)= const, из (10.1 7.18) получаем экспоненциальное распределение
P(t) =exp(- λτ), (8.19)
причем θ =1/ λ - математическое ожидание срока службы (ресурса) или средняя наработка на отказ. Функцию риска теперь можно записать в виде
H(t)= 1-exp(-t/ θ). (8.20)
При функции надежности в виде (10.2 8.19) частота отказов в системе однотипных объектов (поток случайных событий) соответствует дискретному распределению Пуассона

 , N=0,1,2,… λτ > 0. (8.21)
, N=0,1,2,… λτ > 0. (8.21)
Согласно данной формуле, аварии на временном интервале τ (t, t + τ) произойдут N раз с вероятностью Q(N, λτ), а отсутствие аварийных ситуаций (отсутствие отказов) - с вероятностью
Q(0,λτ)=exp(-λτ) (8.22)
Вероятность того, что аварии произойдут n разпри n < N (т.е. менее N раз), определяется функцией распределения
Q0(n<N)= 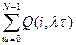 = 1- φ(N,λτ) (8.23)
= 1- φ(N,λτ) (8.23)
φ(N, λτ)= Q0(n≥N)= 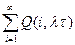 .
.
Вероятность 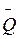 возникновения хотя бы одной аварии представляет оценку риска аварий на объекте в период τ
возникновения хотя бы одной аварии представляет оценку риска аварий на объекте в период τ
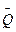 = 1– Q (0, λτ) = 1- exp(- λτ) (8.24)
= 1– Q (0, λτ) = 1- exp(- λτ) (8.24)
Для математического ожидания Ν, дисперсии D и стандарта (среднеквадратического отклонения) σ имеет место равенство N = D = σ 2 = λτ, т.е. имеется возможность экспериментальной проверки правдоподобия гипотезы о применимости закона Пуассона к конкретному виду аварии по факту хотя бы приблизительного соблюдения равенства N =D.
Таким образом, прогнозирование аварийных ситуаций возможно на основе элементарной статистики. Такого рода данные представляют интерес при принятии решений о мерах по снижению степени риска аварий на объектах.
Значения вероятности аварий Q(N, λτ) для числа N ≤ 5 и риска возможной аварии 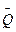 приведены в таблице 8.7 и на рисунке 8.18
приведены в таблице 8.7 и на рисунке 8.18
Вероятность N аварий и оценка риска аварийности 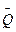 в зависимости от параметра lτ, согласно распределению
в зависимости от параметра lτ, согласно распределению
Пуассона
Таблица 8.7
| N | 0,1 | 0,2 | 0,3 | 0,5 | 1,0 | 2,0 | 3,0 | 4,0 | 5,0 |
| 0,905 | 0,819 | 0,741 | 0,607 | 0,368 | 0,135 | 0,050 | 0,018 | 0,007 | |
| 0,091 | 0,164 | 0,222 | 0,303 | 0,368 | |||||
| 0,0045 | 0,016 | 0,033 | 0,076 | 0,184 | 0,271 | ||||
| 0,0002 | 0,0011 | 0,0033 | 0,013 | 0,061 | 0,180 | 0,224 | |||
| 0,0001 | 0,0003 | 0,0016 | 0,015 | 0,090 | 0, 168 | 0,195 | |||
| 0,0002 | 0,003 | 0,036 | 0,101 | 0,156 | 0,176 | ||||
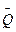
| 0,095 | 0,181 | 0,259 | 0,393 | 0.632 | 0,865 | 0,950 | 0,982 | 0,993 |
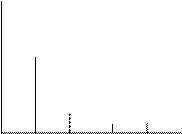
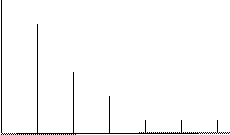
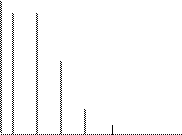
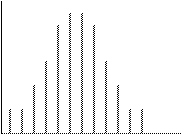
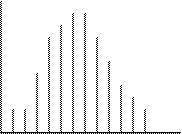
Закон Пуассона является частным (предельным) случаем биномиального распределения при большом числе маловероятных событий. В связи с этим формулу Пуассона называют законом редких явлений. На рис.8.19 показано распределение Пуассона для нескольких значений λτ, из которого видно, что при больших значениях λτ (λτ ³ 10) распределение приближается к нормальному распределению при μ = σ 2 = λτ
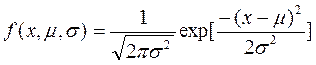 (8.25)
(8.25)
Закон Пуассона широко используют на практике: в теории надежности, при проверке качества, при прогнозировании сейсмического риска и др. Закон Пуассона применим также к событиям (авариям), разбросанным на площадях. В этом случае параметр λ имеет смысл средней плотности, отнесенной не к временному интервалу, а к некоторой площади.

 1,0 1,0
| Q | 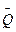
| |||
| 0,8 | |||||
| 0,6 | |||||
| 0,4 | |||||
| 0,2 | N=1 | ||||
| 5,λτ |
Рис. 8.18 Вероятность аварий и оценка риска  аварийности в зависимости от параметра λτ
аварийности в зависимости от параметра λτ




 |  | ||



 0,6 Q 0,3 Q
0,6 Q 0,3 Q
λτ =0,5 λτ =1

 0 2 4 N 0 3 6 N
0 2 4 N 0 3 6 N

 0,2 Q λτ =2 0,15 Q λτ =4
0,2 Q λτ =2 0,15 Q λτ =4
 | |||
 |



 0 3 6 N 0 5 10 N
0 3 6 N 0 5 10 N


 0,12 Q λτ =8 0,1 Q λτ =10
0,12 Q λτ =8 0,1 Q λτ =10
0 10 20 N 0 10 20 N
Рис. 8.19 Распределение Пуассона для шести значений λτ
Известен пример исключительно хорошего согласия с распределением Пуассона реальной статистики падений самолетов-снарядов в южной части Лондона в период второй мировой войны. Такое согласие установлено при подсчете числа kпадений, приходящихся на каждый из Ν = 576 одинаковых участков территории, каждый площадью S = 0,25 км2. При общем числе снарядов Т = 537 число участков Nk, на которое приходилось по k падений (среднее число λS = Т/N - 0,9323), дано в табл. 8.8 в сравнении со значениями вероятностей Р (k; 0,9323), подсчитанных по формуле Пуассона.
Сравнение статистики падения самолетов-снарядов с соответствующим распределением Пуассона
Таблица 8.8
| Число падений k | ≥5 | ||||||
| Число участков Νk, Q (0,9323) 576* Q (k; 0,9323) | 299 0,3936 226,74 | 211 0,3670 211,39 | 93 0,1711 98,54 | 0,0532 30,62 | 7 0,0124 7,14 | 0,0023 1,33 |
Оценку надежности производственных установок и различной аппаратуры, а также обслуживания персоналом можно провести с использованием биноминального распределения подсчетом вероятности как частоты r успешных событий (например, пусков и т.п.) при их общем числе п. Доверительный интервал для фактической вероятности РT определяется уравнением
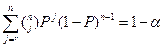
где - 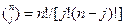 биномиальные коэффициенты; Р - нижняя граница искомой надежности РТ; α - достоверность того, что фактическая вероятность РТ находится в интервале Р...1. Значения вероятности РТ при достоверности α= 0,8 приведены в табл. 8.9для трех значений п.
биномиальные коэффициенты; Р - нижняя граница искомой надежности РТ; α - достоверность того, что фактическая вероятность РТ находится в интервале Р...1. Значения вероятности РТ при достоверности α= 0,8 приведены в табл. 8.9для трех значений п.
Вероятность успешных (безаварийных) событий с
достоверностью 0,8 при различных значениях r
Таблица 8.9
| п | ||||||||||
| 0,083 0,056 0,041 | 0,240 0,157 0,117 | 0,418 0,272 0,201 | 0,619 0,394 0,291 | 0,851 0,524 0,384 | 0,662 0,481 | 0,813 0,582 | 0,686 | 0,798 | 0,922 |
Рассматривается альтернативный подход с привлечением модели, учитывающей некоторые физические процессы, в предположении, что авария на взрывоопасном объекте возникает в результате накопления элементарных повреждений у при достижении некоторого предельно-допустимого износа М. Процесс накопления повреждений фиксируется функцией износа η(t). Отказ наступает при условии η(t) ≥ М, и числе элементарных повреждений r = М/ у.
Для объектов с высокой однородностью начального качества (обеспечивается жестким контролем качества материалов и технологии производства, что обычно реализуется при изготовлении труб, сосудов, резервуаров и газгольдеров) расчет вероятности отказа (аварии) возможен с использованием модели монотонно стареющих систем, т.е. с накапливающимися повреждениями, на основе гамма-распределения времени Т функционирования
F (T) = 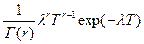
где Г(r) - гамма-функция, λ = y-1dM[η(t)]/dt - скорость износа.
Для целых значений rгамма-функция Г(r) = (г - 1)!,
λ - средняя скорость износа и функция распределения гамма-распределения имеет вид
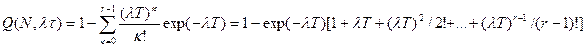 . (8.24)
. (8.24)
При r= 1 выражение (10.9) (7.24) соответствует плотности экспоненциального распределения (мгновенный выход из строя при однократном повреждении).
8.8.1 Примеры оценки риска аварий.
Пример 8.1. На объекте за 20 лет произошло 4 аварии, т. е. среднее число аварий равно λ = 4 / 20 = 0,2 лет-1. Тогда за период τ = 2 года две аварии (N = 2) могут произойти с вероятностью:
Q [(2; 0,2 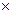 2)] = 0,4 2 exp(-0,4)/2! = 0,054,
2)] = 0,4 2 exp(-0,4)/2! = 0,054,
а одна авария – с вероятностью Q (1; 0,4) = 0,227.
Вероятность безаварийного функционирования объекта Q (0; λτ) в течение двух лет равна Q (0;0,4) = ехр(-0,4) = 0,67, а в течение одного года Q (0;0,2) = ехр(-0,2) = 0,82, т. е. риск аварийных ситуаций за двухлетний период составит 1- 0,67 = 0,33, а за один год 0,18.
Пример 8.2Средняя скорость износа агрегата с взрывоопасным энергоносителем λ = 0,02 ч - 1. Предельное число элементарных повреждений τ = 6. Агрегат функционирует 3 ч в сутки. Определим риск аварий в течение недели.
За указанный срок время работы агрегата Т = 7 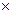 3 = 21 ч, λТ = 0,42. По формуле (10.9) оценка величины риска:
3 = 21 ч, λТ = 0,42. По формуле (10.9) оценка величины риска:
R (0,42) = 1- exp(-0,42)(1+ 0,42+ 0,422/2+ 0,423/6+ 0,424/24+ 0,425/120) = 5,33 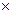 10-6.
10-6.
Date: 2015-07-17; view: 3259; Нарушение авторских прав