Тема 1. Гармонические колебания

Гармонические колебания — это колебания, при которых координата (смещение) тела изменяется со временем по закону косинуса или синуса и описывается формулами:

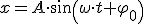
Зависимость координаты от времени x(t) называется кинематическим законом гармонического колебания (законом движения). Графически зависимость смещения колеблющейся точки от времени изображается косинусоидой (или синусоидой).

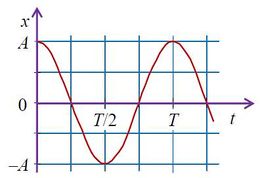
Пусть тело совершает колебания по гармонические закону (φ₀ = 0). На рисунке 1 представлен график зависимости координаты x от времени t.

1)

Выясним, как изменяется проекция скорости колеблющейся точки со временем. Для этого найдем производную по времени от закона движения:

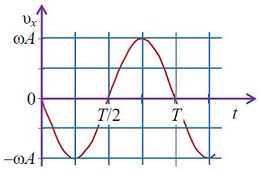
где 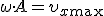— амплитуда проекции скорости на ось x. Эта формула показывает, что при гармонических колебаниях проекция скорости тела на ось x изменяется тоже по гармоническому закону с той же частотой, с другой амплитудой и опережает по фазе смешение на π/2 (рис. 2).

2)

Для выяснения зависимости ускорения a_x(t) найдем производную по времени от проекции скорости:

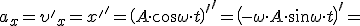
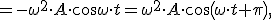(1)

где — амплитуда проекции ускорения на ось x.

При гармонических колебаниях проекция ускорения опережает смещение по фазе на π (рис.3).

3)

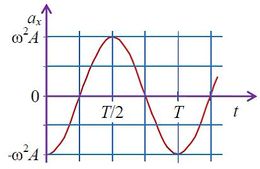
Аналогично можно построить графики зависимостей x(t), υ_x(t) и a_x(t), если 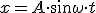(φ₀ = 0).

Учитывая, что 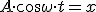из уравнения (1) для ускорения можно записать

т.е. при гармонических колебаниях проекция ускорения прямо пропорциональна смещению и противоположна ему по знаку, ускорение направлено в сторону, противоположную смещению. Данное соотношение можно переписать в виде

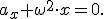
Последнее равенство называют уравнением гармонических колебаний. Физическую систему, в которой могут существовать гармонические колебания, называют гармоническим осциллятором, а уравнение гармонических колебаний — уравнением гармонического осциллятора.

Date: 2015-06-11; view: 503; Нарушение авторских прав