
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Числа Фибоначчи в анализе Эллиота
|
|





 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584
1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584
     | |||||||||
 |  |  |  | ||||||
Рис.2. Одна из авторских интерпретаций иллюстрации связи между последовательностью Фибоначчи и компонентами фрактальной модели Эллиота. Обратите внимание на то, что волна данной степени соответствует четному числу Фибоначчи и состоит из импульса и коррекции, которым сопоставляются 2 предыдущих нечетных члена последовательности.
Перед тем как продолжить, необходимо дать точное определение терминов, которые будут использоваться в дальнейшем. Любое циклическое явление характеризуется периодом, частотой и амплитудой. Частота представляет собой число циклов в единицу времени; периодом является величина ей обратная (время одного полного цикла), а амплитуда описывает размах колебаний. Важно отметить, что период цикла должен быть величиной строго постоянной – либо мы не имеем права называть явление циклическим. В этом смысле теория Эллиота не работает с циклами, так как здесь каждой волне приписываются уникальные свойства, не относящиеся ни к направлению ее, ни ко времени (временной оси). Сама суть фрактальной природы основополагающей модели вообще и всех ее составляющих в частности требует индивидуальной интерпретации каждой конкретной волны по отношению ко всем остальным. Это – основы проводимой на данном теоретическом базисе аналитической работы.
Именно поэтому эллитовцы оперируют не периодами, а частотами волн. К частотам же относятся все применяемые в теории соотношения Фибоначчи и вообще все производимые расчеты. Кстати, обратили ли Вы внимание на то, что волны Эллиота в действительности являются полуволнами (они однонаправлены)? Одно из многих необычных и очень полезных свойств последовательности Фибоначчи заключается в том, что для их практического применения к теории Эллиота совершенно неважно, целыми волнами оперировать или же половинами их.
В теории Эллиота вводится понятие нумерации волн. Здесь имеются в виду числовые обозначения векторных составляющих модели. На рис.3 фрактальная модель изображена уже в "пронумерованном" виде: каждой волне определенной степени в пределах данной детализации сопоставлены соответствующие числа последовательности Фибоначчи. Такая модель называется волновой диаграммой Пречтера.
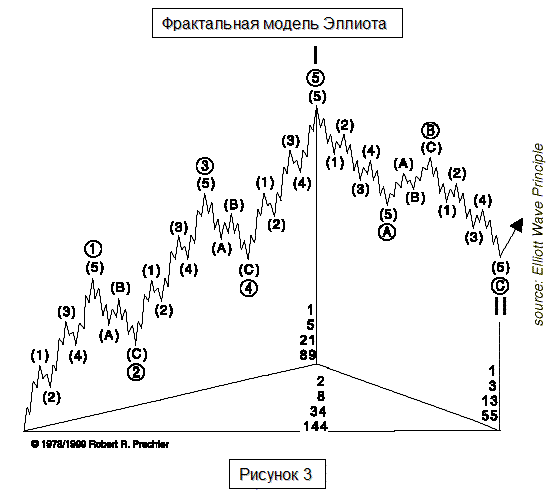 |
Рис. 3. Волновая диаграмма Пречтера для нескольких степеней волн Эллиота с нумерацией по Фибоначчи.
ГАРМОНИЯ И ГАРМОНИЧНОСТЬ
Несмотря на то что соотношения Фибоначчи чрезвычайно распространены как в природе, так и в разнообразных видах человеческой деятельности, циклисты (а также физики и инженеры) отмечают широкий ареал действия и некоторых других соотношений и законов. Необходимо добавить, что никто с ними и не спорит по этому поводу. В частности, существуют физические силы, приводящие систему в колебательное (циклическое) движение вроде колебаний маятника. В частности же, когда энергия одной системы сообщается другой, системы эти могут войти в резонанс: при пропорциональности частот возникают гармонические колебания. Люди точно так же склонны к эмоциональным колебаниям, которые являются движущими силами их действий и инициируют активность сторонних сил: мы обдумываем поступающую извне информацию и определенным образом реагируем на нее, а наши действия, в свою очередь, вызывают последствия, иногда предсказуемые заранее. Поразмыслите над словом "гармония, гармоничность" – его можно определить как "соразмерность частей, слияние различных компонентов системы в единое целое" и как "нечто, отмеченное согласованностью побуждения и действия". Люди, взятые по отдельности, подвластны влиянию толпы – как и у всех высокоорганизованных животных, у нас очень сильно развит стадный инстинкт. Толпа действует синхронно, как единый социальный организм. Гармоничные отношения отличаются согласованностью, и частоты гармоничных процессов и явлений находятся в целочисленном отношении друг к другу. Примером синхронизированой с внешней средой системы может служить человеческое ухо – инструмент для улавливания и преобразования звуковых колебаний в "химическую" информацию для рецепторных клеток, опосредующих высшую нервную деятельность. Примеров можно привести великое множество – и имеющих отношение к рынкам в том числе (что уже само по себе интересно). Старые афоризмы "тренд – Ваш друг", "не спорьте с рынком" являют собой простое качественное определение основных принципов функционирования в гармонии либо в конфликте с текущими движущимися силами системы.
Именно размышления о пропасти, разделяющей циклистов и эллиотовцев, явились отправной точкой настоящего исследования. Ведь если только допустить, что оба рассматриваемых подхода к анализу биржевой ситуации имеют под собой разумную основу и дают обоснованные результаты, тогда, по всей вероятности, можно допустить и то, что они не так уж и взаимоисключающи, как это кажется. (Свежий взгляд на проблему с новой неожиданной стороны зачастую помогает разрешить ее). Если это заключение верно, то появляется возможность совместной работы двух наших конфликтующих дисциплин в будущем и улучшения каждой из них путем интеграции отточенных аналитических инструментов, применяемых в обеих.
Задача моя состоит в демонстрации связи между теориями. Освещаемый здесь процесс ее выполнения был нарочно упрощен с помощью использования продолжения моей предыдущей работы по созданию условных ценных бумаг, описанной в предыдущих номерах журнала (метод компьютерного моделирования). В число моих основных аналитических инструментов также вошли такие программные продукты, как MetaStock v.6.5.2 и WinWaves32 от "Equis International" и "International Trading" соответственно.
ФРАКТАЛЬНАЯ МОДЕЛЬ ЭЛЛИОТА
Сначала необходимо найти такое сочетание синусоидальных кривых, с помощью которого можно получить идеальную фрактальную модель – основную, исходную структуру классического анализа по Эллиоту (смотрите рис.1). Считаю необходимым удержаться от искушения (устоять перед искушением) начать с линейных компонентов вектора: простая схожесть с оригиналом ничего не даст в плане обоснования как самого оригинала, так и модели его относительно их применимости к реальной биржевой ситуации. Это разрушило бы все мои планы – ведь цель исследования заключается в обнаружении связи между теориями волн Эллиота и циклов.
В своей предыдущей работе я продемонстрировал, как сочетание нескольких синусоидальных кривых может породить самые причудливые формы волн; материалом для нее послужили данные о рынке ценных бумаг компании "Alaska Airlines", а количество синусоид, использовавшихся для моделирования, равнялось трем. Должно быть, это и есть то минимальное количество, с которого можно начать процесс поиска компонентов идеализированной фрактальной модели. На следующем рисунке показана основная циклическая составляющая данной модели – базиса моего исследования (линейные графики используются исключительно для простоты). За аксиому принята исчерпывающая информативность и вполне достаточная значимость для целей данного исследования сведений о ценах на момент закрытия биржи. Исходные синусоидальные компоненты представлены в левой нижней части каждого графика. Их амплитуды, частоты и фазы соответствуют аналогичным значениям результирующих волн, показанных в верхней части.
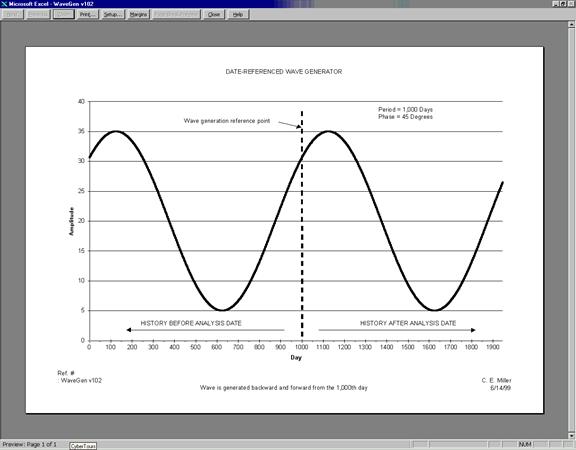
Рис.4. Базисные синусоидальные кривые – циклические компоненты, моделирующие структуру Эллиота. Использование линейных графиков обусловлено применением данных о котировках на момент закрытия биржи.
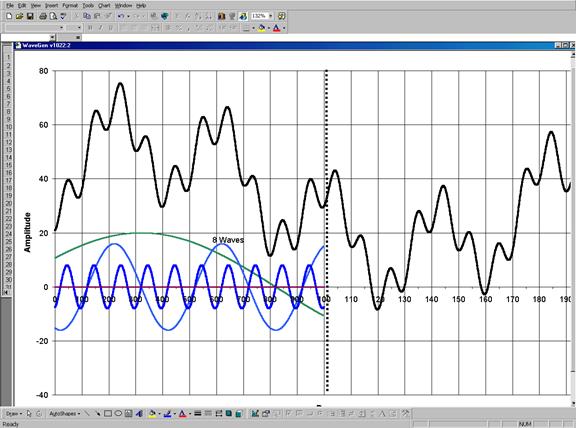
На удивление быстро я нашел верное сочетание синусоид. Оказалось, что для получения фундаментальной 5-3 волновой структуры Эллиота требуются всего лишь две "циклоиды" с нулевым сдвигом по фазе, периоды которых соотносятся как 4:1, а амплитуды – как 2:1. Эти кривые представлены на рис.5.
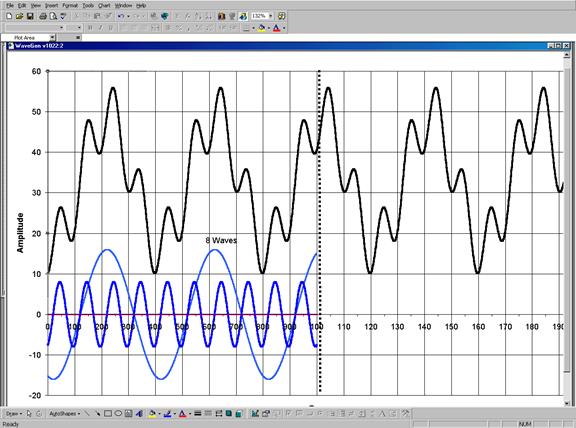
Рис.5. Основополагающая структура теории Эллиота, состоящая из 8 волн (5 в направлении тренда и 3 против) образована всего лишь двумя синусоидами с постоянными периодами, частоты которых находятся в отношении 4:1, а амплитуды – 2:1, сдвиг фаз отсутствует.
В дополнение к рассмотренным модель Эллиота обладает и другими важными свойствами. Во-первых, она фрактальна: определенное количество однородных волн образует степень, определенное количество волн этой степени образует более высокую степень и т.д., причем формы волн связаны отношением подобия: они бесконечно повторяются в пространственном отношении, различаясь лишь масштабом. Вторая интересная особенность заключается в том, что третья волна импульса (направление тренда возрастающее) превышает по длине его первую или пятую компоненту.
Заинтересовавшемуся читателю я посоветовал бы зайти в Институт им. Р. Н. Эллиота. Такого количества литературы по теории волн Вы не найдете нигде. Вы сможете не просто поверхностно ознакомиться с этой теорией, но и узнаете, как практически применять ее в реальных биржевых операциях. В частности, краткий вводный курс (101) и исчерпывающий детальный (201) могут пройти оперативно (и бесплатно) все желающие.
Тем же, кто знаком с теорией Эллиота не понаслышке и уже использует ее для своей повседневной биржевой деятельности, должно быть известно и то, что лучше всего она "работает" на трендовых рынках. Давайте вместе разберемся, так ли это – и если да, то почему. Вернемся вновь к рис.5. На первый взгляд может показаться, что изображенная на нем структура отражает лишь рост либо падение котировок. Однако стоит только вспомнить о принципах ее построения (бесконечно повторяющийся в пространственном отношении типаж), как станет ясным тот факт, что график в действительности лишен какой-либо направленности: достаточно сильные колебания не имеют никакой определенной тенденции. Таким образом, можно заключить, что теория показывает одинаково хорошие результаты на всех типах рынков, и на нетрендовых в том числе.
Из сделанного нами только что наблюдения непосредственно вытекает необходимость введения еще одной составляющей: долгосрочного линейного компонента, отражающего в первом приближении глобальную направленность тренда. Полученный результат иллюстрирован на рис.6.
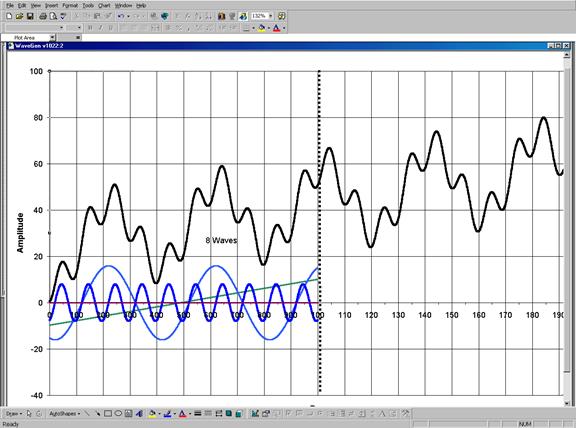
Рис. 6. Модель трендового рынка получается при помощи последовательного сложения синтетических синусоидальных волн, изображенных на рис.5, с наклонной прямой, отражающей в первом приближении направление тренда.
Итак, к настоящему моменту нам удалось синтезировать последовательность волн Эллиота. Оказалось, что для создания фундаментального фрактала достаточно сложить всего лишь две гармоничные, синхронные и пропорциональные синусоиды (2 цикла). Направление долгосрочного тренда, фактически представляющего собой структуру Эллиота более высокой степени, в первом приближении моделируется наклонной прямой. На рис.6 изображен случай роста котировок. Очевидно, что в противоположной ситуации знак угла наклона этой "идеализированной суммы долгосрочных компонентов" должен быть изменен на противоположный – для случая их понижения существует симметрия относительно оси х. Эта ситуация представлена на рис. 7.
.
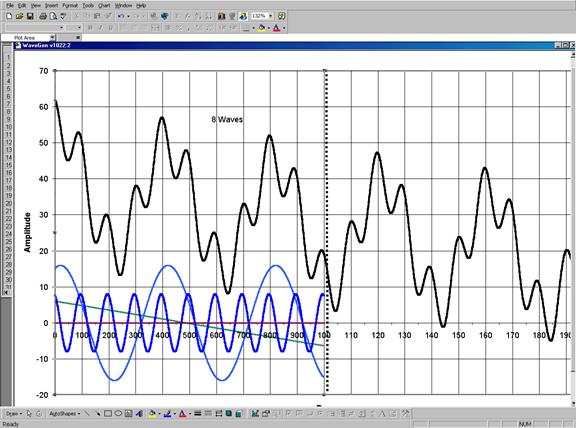
Рис. 7. Случай понижения котировок: знак угла наклона прямой, представляющей собой идеализированную сумму долгосрочных компонентов, изменен на противоположный.
ПРОБЛЕМА ТОЧКИ МАКСИМУМА
{{Примечание редактора: выделенные жирным/подчеркнутые буквенно-цифровые обозначения рисунков следующего параграфа и обозначения, используемые в заголовке рис.8, не вписываются в общую нумерацию статьи. Для соответствия с ней необходимо прибавлять ноль перед цифрой.}}
Структура Эллиота фрактальна – волна любой степени имеет одинаковую форму. С помощью двух синусоид можно моделировать ненаправленные волны, с помощью наклонной прямой можно сделать их однонаправленными, но для отражения фрактальной природы модели этого недостаточно. Выше мы говорили о том, что порядок следования структурных составляющих тверд и нерушим (5-3). Пришло время признать, что в этом правиле, как и в любом другом, есть свои исключения.
Часть рис.1, обозначенная как 5-А, была специально вынесена в отдельную иллюстрацию для того, чтобы показать, что третья ее часть (фрактал) имеет нетипичную нумерацию: "5-5" вместо обычных "5-3". Эллиот объяснял это тем, что волна А данного фрактала движется против тренда степенью выше. Направление ее движения показано стрелкой (от волны С и II к началу волны lll).
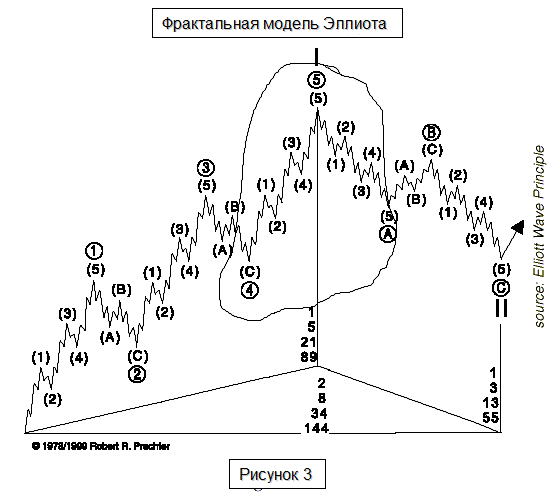 |
Рис.10. Выделенный фрагмент представляет собой часть рис.1 – волну 5-А. Вы заметили, что составляющие ее подволны пронумерованы как "5-5" вместо обычных "5-3"? Именно это приводит к расхождениям циклистов и эллиотовцев в цифровых обозначениях волн: из-за этих 2х волн нумерация по Эллиоту не совпадает с циклической и опережает ее на 2.
Применение 34-волновой нумерации (по Фибоначчи) вместо 32-волновой, используемой в теории циклов – еще одно из основных правил Эллиота – это еще одна проблема для аналитика, но не причина считать саму идею ошибочной. Сложим с фундаментальными синусоидальными кривыми, изображенными на рис.5, волну большей (в 16 раз) частоты – 32-волновая структура циклистов получится в результате. (Она изображена на рис.9.)
Важно отметить, что разрешение теорией циклов этой двух волновой аномалии ни в коем случае не допускает изменений оригинальной структуры, состоящей из двух синусоид, моделирующих базисную 5-3 волновую структуру Эллиота меньшей степени: значение любого числа Фибоначчи является суммой двух предыдущих членов последовательности (смотрите рис.2).
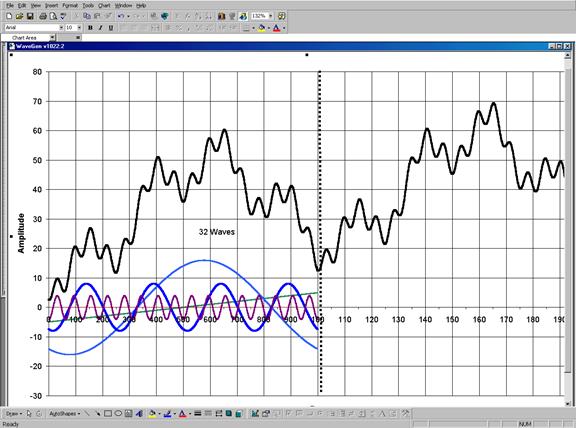
Рис.9. Сложение третьей гармонической синусоиды с более низкой амплитудой и высокой частотой с компонентами структуры, показанной на рис.5, моделирует цикл, состоящий из 32 волн. Это соответствует правилам теории циклов и расходится с правилами теории волн: Эллиот установил, что число компонентов данной модели должно равняться тридцати четырем (34).
Обсудив причины, по которым Эллиот изменил свою фундаментальную структуру вне зависимости от того, что в соответствии с его же твердыми и нерушимыми правилами делать этого нельзя было ни в коем случае, мы вынуждены заключить, что циклистам ничего другого не остается, как последовать его примеру. Спешу заверить умного, но утомленного читателя, что эта операция не нарушит и не разрушит ни одной из равновесных циклических составляющих исходной модели. Наиочевиднейшим изменением была бы десинхронизация частотных соотношений "новой" волны и компонентов 5-3 волновой структуры.
Увеличение частоты самой низкоамплитудной волны изменит 32-волновую нумерацию циклистов на 34-волновую эллиотовцев (смотрите рис.10). Таким образом, мы обнаружили недостающее связующее звено – это яблоко раздора двух столь близких по духу теорий, считающих себя противоположными полярно. Скорее всего именно нежелание последователей Эллиота учитывать при моделировании негармонические колебания и было первой трещиной в той пропасти, которая разделяет сейчас два эти лагеря.
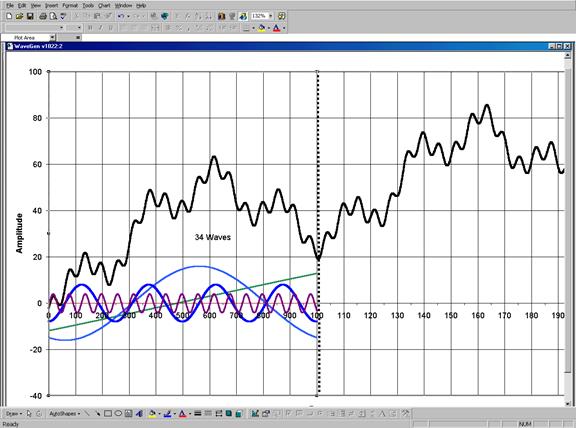
Рис. 10. 34-волновой цикл Эллиота в точности воспроизводится сложением третьей синусоидальной кривой с компонентами модели, изображенной на рис.9. вновь введенная синусоида характеризуется постоянным периодом и частотой, приблизительно в 16 раз превышающей базисную и обладает минимальной из всех амплитудой.
Я считаю большим достижением сам факт точного соответствия компьютерной модели 21-13-волнового цикла Эллиота оригиналу. Он доказывает необходимость и достаточность введения негармонической циклической составляющей. Достаточность, я надеюсь, очевидна, поэтому сейчас мы поговорим о необходимости.
Допустив на мгновение, что Эллиот ошибался и связи между его фракталами и последовательностью Фибоначчи нет, мы, казалось бы, упростим задачу, избавившись от негармонического синусоидального компонента. К сожалению, абсолютно гармонические соотношения воспроизводят ситуацию, далекую от реальной, что явным образом ограничивает применимость модели (смотрите рис.9). Этот неоспоримый аргумент эллиотовцев свидетельствует в их пользу.
Обратите внимание на то, что введенный нами негармонический компонент является наименьшей из волн (по амплитуде, обратно пропорциональной частоте). Как следствие, он оказывает минимальное влияние на общую форму модели и может быть интерпретирован как влияние на рынок высокомобильной группы трейдеров – таких, например, как дневные (они же внутридневные). Их биржевая деятельность имеет второстепенное значение для формирования тренда, однако сам ее характер обусловливает чувствительность к изменениям его направления и высокую скорость реакции на них. Активность таких трейдеров не утихает и в тех случаях, когда рынок "идет против тренда". Для этой группы характерна взаимовлияемость и синхронность, что создает отчетливые подуровни характерной данному рынку волатильности.
Тот факт, что негармоническая синусоида имеет некоторый сдвиг по фазе относительно двух гармонических, не противоречит основным положениям волновой теории: внешний вид волн может отличаться от идеальной модели, но численные обозначения должны соответствовать ей всегда. Именно по этой причине Эллиоту пришлось разрабатывать многочисленные правила и руководства.
Далее, цикличность искусственно синтезированной структуры не нарушается, более того – воспроизводится ее фрактальность. Следующая степень насчитывает 144 волны. Как Вы помните, в предыдущий раз для получения числа Фибоначчи (34) пришлось "добавить" 2 дополнительных волны в структуру из 32. Интересно отметить, что сложение с ними еще одной волны с частотой в 4 раза большей, чем у введенной в рис.10, приведет к результату на 8 волн короче, то есть 144-(4*34). Это позволяет сделать предположение о том, что для каждой следующей степени деления нам придется добавлять волну с частотой, определяемой по формуле
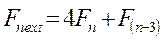 |
Заметили ли Вы, что это одно из чисел последовательности Фибоначчи? Обратите также внимание на постоянно встречающуюся (а следовательно, важную) цифру 4 и на то, что все числа Фибоначчи подчиняются отношению
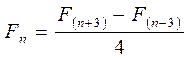 |
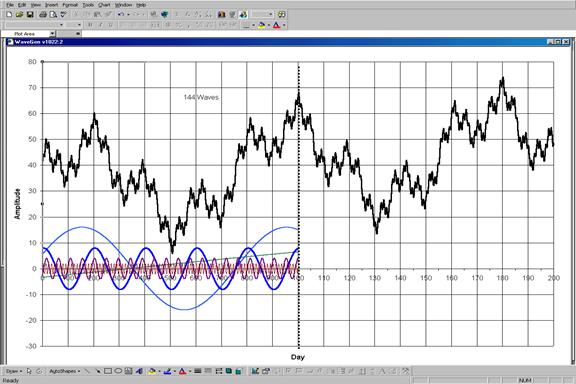 |
Таким образом добавление волны с пропорционально меньшей амплитудой и частотой, вычисляемой по формуле (1), позволяет нам обобщить 34х-волновую структуру Эллиота (рис.10) на 144х-волновой случай (рис.11).
Рис.11. Структура, состоящая из 144 волн Эллиота, может быть смоделирована сложением волны с частотой, определяемой равенством (1), с компонентами 34-волновой структуры, представленной на рис.10. Сравните этот рисунок с фрактальной моделью Эллиота в обработке Пречтера (рис.3).
ИЗМЕНЕНИЕ НАПРАВЛЕНИЯ ТРЕНДА И ЕГО МОДЕЛИРОВАНИЕ
Мы уже упоминали о том, что все движения рынка в одну-единственную схему уложить очень трудно: всегда находится нечто необъяснимое, предоставляющее непреодолимые трудности для анализа – это знакомо каждому аналитику. Строго говоря, мы знаем лишь то, что котировки периодически растут (но не до бесконечности) и падают (но не ниже нуля), а обо всем остальном лишь догадываемся. Допустим, что синусоида с рис.4 представляет собой влияние, оказываемое на котировки акций силами спроса и предложения, характеризующимися большой амплитудой и низкой частотой. Между максимумами эта могущественная сила движет как волатильные, так и неволатильные цены быстро вверх или вниз. В самих точках максимума, однако, она перестает действовать, и котировки постепенно растут либо падают. Так и протекает процесс изменения направления тренда. Изменения условий с повышения на понижения на простейших диаграммах теории волн имеют вид буквы "Л", а наоборот --- буквы "V". Конечно, реальная рыночная ситуация намного сложнее и зависит от далеко не столь очевидных движущих сил, а изменения происходят не вдруг: например, волна Эллиота никогда не завершается, а всегда является частью какой-то более крупной волновой структуры. Пришло время усложнить и наш анализ. До сих пор направленность рынка моделировалась наклонной прямой. Теперь мы заменим ее синусоидальной кривой (смотрите рис.12, 13).
Рис. 12. Изменение направления тренда, моделируемого 34-волновой структурой Эллиота, с положительного на отрицательное (рост котировок сменяется их падением). Долгосрочный компонент вектора изменений представлен не наклонной прямой, как на рис.10, а синусоидальной кривой.
 |
Рис. 13. Изменение направления тренда (34х-волнового цикла Эллиота) с отрицательного на положительное (с понижения котировок на повышение).
При прохождении волны через максимум мы получаем то искажение идеальной модели, какое и ожидали получить. Помните замечание о том, что теория Эллиота лучше всего работает на трендовых рынках? Несмотря на верность числовых обозначений волн, "отклонение" некоторых из них от нормы может сделать процесс идентификации волн чрезвычайно сложным и трудным безотносительно от способа его проведения (на компьютере или же вручную). Именно такими отклонениями Пречтер и Херст объясняют появление многих стандартных для технического анализа фигур ("голова на плечах", например) на графике котировок в момент изменения направления рынка с повышения на понижение (смотрите рис.13).
Теперь мы можем объяснить, почему анализ графика котировок в теории волн должен начинаться с точки последнего глобального минимума или максимума: это позволяет нам выйти из рамок повседневности и переключить внимание на более продолжительный временной период, давая тем самым теоретической модели (и компьютерной программе) возможность полностью реализовать себя.
Вообще-то такая программа (WinWaves32) предназначена для идентификации всевозможных типов волн, на основе чего составляются прогнозы дальнейшего движения цен. Но специфика данного исследования допускает ее применение с целью познавательной: мы работаем с идеализированной моделью Эллиота, с "идеальными" типами волн, и знаем, как вся волновая структура поведет себя в дальнейшем. WinWaves32 этого знать не может, и условные ценные бумаги можно использовать для проверки аналитических возможностей программы (особенно при исследовании таких ситуаций, в которых теория Эллиота, как говорят, хуже всего работает).
Date: 2015-06-11; view: 563; Нарушение авторских прав