Нахождение угла между векторами, примеры и решения

Косинус угла между векторам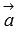и и 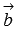, а значит и сам угол, в общем случае может быть найден либо с использованием скалярного произведения векторов, либо с использованием теоремы косинусов для треугольника, построенного на векторах 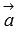и .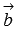

Разберем эти случаи.

По определению скалярное произведение векторов есть 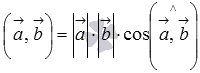. Если векторы 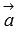и 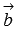ненулевые, то можно разделить обе части последнего равенства на произведение длин векторов 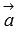и 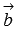, и мы получим формулу для нахождения косинуса угла между ненулевыми векторами: 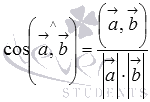. Эту формулу можно использовать, если известны длины векторов и их скалярное произведение.

Пример.

Вычислите косинус угла между векторам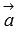и и 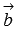, а также найдите сам угол, если длины векторов 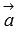и 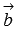равны 3 и 6 соответственно, а их скалярное произведение равно -9.

Решение.

В условии задачи даны все величины необходимые для применения формулы 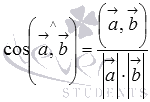. Вычисляем косинус угла между векторам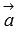и и : .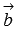

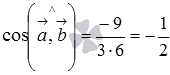Теперь находим угол между векторами: .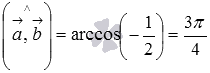

Ответ:

.

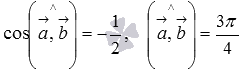Намного чаще встречаются задачи, где векторы заданы координатами в прямоугольной системе координат на плоскости или в пространстве. В этих случаях для нахождения косинуса угла между векторами можно использовать все ту же формулу 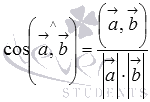, но в координатной форме. Получим ее.

В статье вычисление длины вектора мы выяснили, что длина вектора есть корень квадратный из суммы квадратов его координат, а в разделе скалярное произведение в координатах мы показали, что скалярное произведение векторов равно сумме произведений соответствующих координат. Следовательно, формула для вычисления косинуса угла между векторами 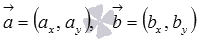на плоскости имеет вид 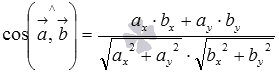, а для векторов 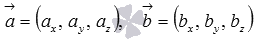в трехмерном пространстве - .

Разберем на примерах.

Пример.

Найдите угол между векторами 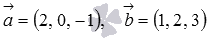, заданными в прямоугольной системе координат.

Решение.

Можно сразу воспользоваться формулой :

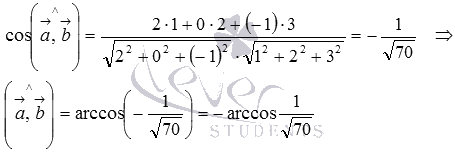
А можно для нахождения косинуса угла между векторами использовать формулу 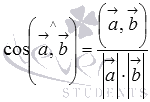, предварительно вычислив длины векторов и скалярное произведение по координатам:

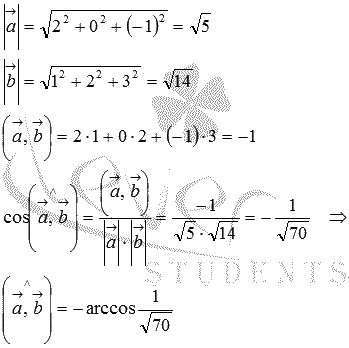
Ответ:

.

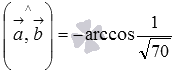К предыдущему случаю сводится задача, когда даны координаты трех точек (например А, В и С) в прямоугольной системе координат и требуется найти какой-нибудь угол (например, ).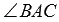

Действительно, угол 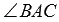равен углу между векторам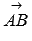и и 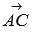. Координаты этих векторов вычисляются как разность соответствующих координат точек конца и начала вектора, об этом мы говорили в статье нахождение координат вектора через координаты точек.

Пример.

На плоскости в декартовой системе координат заданы координаты трех точек 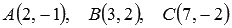. Найдите косинус угла между векторам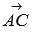и и .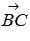

Решение.

Определим координаты векторов 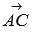и 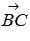по координатам заданных точек:

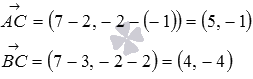
Теперь воспользуемся формулой для нахождения косинуса угла между векторами на плоскости в координатах:

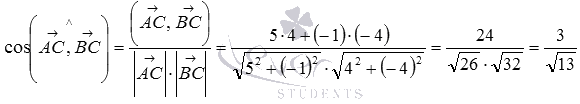
Ответ:

.

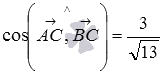Угол между векторам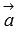и и 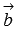также можно вычислить по теореме косинусов. Если отложить от точки O векторы 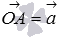и 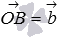, то по теореме косинусов в треугольнике ОАВ мы можем записать 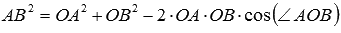, что эквивалентно равенству 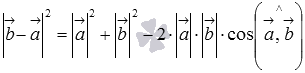, откуда находим косинус угла между векторами 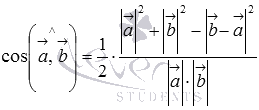. Для применения полученной формулы нам нужны лишь длины векторов 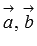и 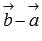, которые легко находятся по координатам векторов 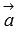и 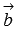. Однако, этот метод практически не используется, так как косинус угла между векторами проще найти по формуле .

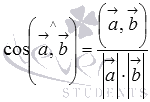Date: 2015-07-17; view: 930; Нарушение авторских прав