Теоретические основы работы

Лабораторная работа №6

ИССЛЕДОВАНИЕ АМПЛИТУДНО МОДУЛИРОВАННОГО СИГНАЛА С ПОМОЩЬЮ ОСЦИЛЛОГРАФА

ЦЕЛЬ РАБОТЫ

Ознакомление с принципами амплитудной модуляции. Приобретение экспериментальных навыков исследования электрических процессов с помощью электронного осцил-лографа. Исследование амплитудно модулированного сиг-нала, определение глубины модуляции и добротности коле-бательной системы.

ТеоретическИе ОСНОВЫ РАБОТЫ

Амплитудная модуляция применяется в радиосвязи при передаче и приеме звукового сигнала на декаметровом и более низкочастотных диапазонах радиоволн. Принцип ам-плитудной модуляции заключается в наложении низкочас-тотных колебаний (передаваемый сигнал) на высокочастот-ные (несущая частота).

Пусть величина тока в колебательном контуре изменя-ется по гармоническому закону:

. (6.1)

При наложении низкочастотного сигнала (частотой ) из-менения тока в контуре превращаются в более сложные ко-лебания, амплитуда которых начинает сравнительно мед-ленно меняться с частотой :

, (6.2)

где – модулирующая функция, причем .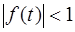

Тогда имеем:

, (6.3)

т.к. частота модуляции 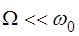( 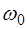– несущая частота), то ко-лебание (6.3) можно рассматривать как гармоническое, име-ющее амплитуду 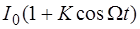. Максимальное и минимальное значение амплитуды: , .

Величина

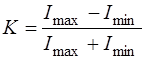(6.4)

называется глубиной модуляции (рис. 6.1).

После преобразования выражения (6.3) можно получить:

. (6.5)

Таким образом, модулированное колебание (6.5) пред-ставляет собой три гармонических колебания, происходя-щих с частотам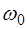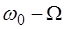и , и 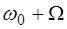(рис. 6.2).

Основная частота 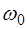называется несущей частотой, а до-полнительные частоты (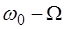) и (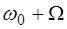), возникающие при модуляции – боковыми частотами.

Величина называется шириной спектра модулирован-ного сигнала.

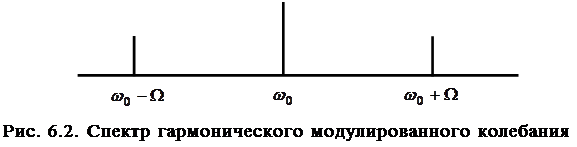Любой приемник радиосигнала имеет на входе колеба-тельный контур, настроенный в резонанс с несущей час-тотой. Поэтому, изменяя несущую частоту, мы изменяем амплитуду принимаемого сигнала, что можно видеть на эк-ране осциллографа. Измерив зависимость амплитуды сигна-ла от несущей (высокой) частоты, можно определить резо-нансную частоту контура и его добротность. Амплитудный модулятор, используемый в работе, тоже имеет колебатель-ный контур. Принципиальная схема амплитудного модуля-тора показана на рис. 6.5, колебательный контур модуля-тора состоит из катушки индуктивности L_К и емкости С_К.

Добротность колебательной системы определяется выра-жением:

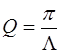, (6.6)

где Λ – логарифмический декремент затухания, который, в свою очередь, рассчитывается как:

. (6.7)

В выражении (6.7) β – коэффициент затухания; T – пери-од затухающих колебаний.

Подставив в (6.6) выражение (6.7) и, учитывая связь между периодом и частотой колебаний, получим:

, (6.8)

где 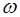– частота вынуждающей силы.

При малых затуханиях (β <<1) частота колебаний при-мерно равна собственной (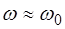), что позволяет записать:

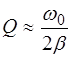. (6.9)

Амплитуда вынужденных колебаний зависит от частоты:

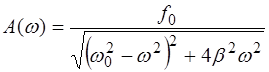, (6.10)

где f₀ зависит от амплитуды вынуждающей силы: 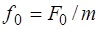в случае механических колебаний; 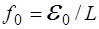в случае элек-трических колебаний. Здесь F₀ – максимальное значение вынуждающей силы; m – масса колеблющегося тела; ε₀ – максимальное значение вынуждающей ЭДС; L – индуктив-ность контура.

Итак, измерив амплитуду A_рез при резонансе контура и значения амплитуды на частотах 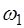и 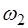, отстоящих на ве-личину β от резонансной частоты, можно рассчитать доб-ротность контура.

Резонанс в колебательной системе наступает при частоте

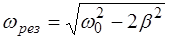, (6.11)

однако при малых затуханиях можно считать, что резонанс-ная частота примерно равна собственной .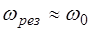

Тогда, введя

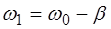и 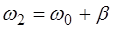, (6.12)

можно записать, что

. (6.13)

С учетом этого выражение (6.9) принимает вид:

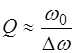. (6.14)

Для того, чтобы определить 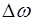, рассчитаем, чему равна амплитуда колебаний на частотах 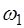и 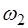. Точнее, мы определим отношение амплитуды A_1,2 колебаний на часто-тах 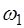и 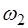к амплитуде колебаний при резонансе A_рез.

Подставив выражение (6.11) в (6.10) определим резо-нансную амплитуду:

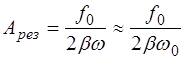. (6.15)

Для определения амплитуды A_1,2 (а амплитуда на часто-тах 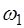и 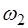будет одинаковой, это видно из симметрич-ности значений знаменателя в (6.10)) подставим в (6.10) выражение:

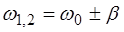. (6.16)

Поскольку числитель (6.10) есть величина постоянная, рассчитаем подкоренное выражение в знаменателе:

.

Раскрыв скобки, получим

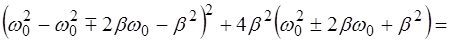
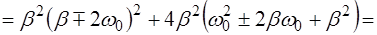
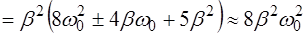(6.17)

При получении выражения (6.17) мы пренебрегли слага-емыми, содержащими коэффициент затухания β вследствие его малости. Итак, амплитуда колебаний на частотах 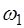и 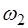будет:

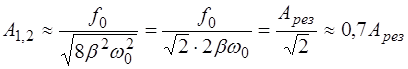(6.18)

Итак, для определения добротности колебательной сис-темы по формуле (6.14) необходимо определить резонанс-ную частоту 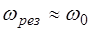, то есть ту частоту, для которой амп-литуда максимальна, и две частоты 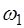и 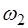, на которых ам-плитуда равна 70% от максимальной. На рис.6.3 показана амплитудно-частотная характеристика колебательной сис-темы, позволяющая определить добротность этой системы с использованием формулы (6.14).

Date: 2015-06-11; view: 383; Нарушение авторских прав