
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Электромагнитные волны
|
|
8.1 Уравнения Максвелла
В середине 19-го века Максвеллом была завершена те-ория электромагнитного поля. Было выяснено, что элект-рическое и магнитное поле являются проявлениями еди-ного электромагнитного поля. Электромагнитное поле в неподвижных средах описываются так называемыми фун-даментальными уравнениями Максвелла.
В дифференциальном виде уравнения Максвелла выглядят следующим образом:
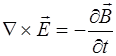 ,
,
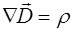 ,
,
(8.1)
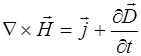 ,
,
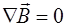 ,
,
где  – вектор напряженности электрического поля;
– вектор напряженности электрического поля;
 – вектор индукции магнитного поля;
– вектор индукции магнитного поля;
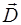 – вектор электрического смещения;
– вектор электрического смещения;
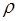 – объемная плотность сторонних зарядов;
– объемная плотность сторонних зарядов;
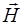 – вектор напряженности магнитного поля;
– вектор напряженности магнитного поля;
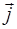 – вектор плотности токов проводимости;
– вектор плотности токов проводимости;
Используемое в системе (8.1) обозначение 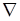 – это опе-ратор Гамильтона (набла). В декартовых координатах оператор Гамильтона равен:
– это опе-ратор Гамильтона (набла). В декартовых координатах оператор Гамильтона равен:
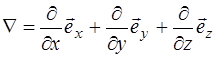 . (8.2)
. (8.2)
В системе (8.1) 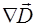 и
и 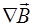 – дивергенции векторов
– дивергенции векторов 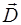 и
и  соответственно. Рассчитывается как скалярное произ-ведение оператора (набла) на вектор. В декартовых коор-динатах указанные дивергенции равны:
соответственно. Рассчитывается как скалярное произ-ведение оператора (набла) на вектор. В декартовых коор-динатах указанные дивергенции равны:
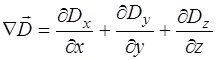 , (8.3)
, (8.3)
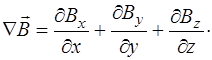 (8.4)
(8.4)
В системе (8.1) 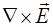 и
и 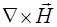 представляют собой роторы векторов
представляют собой роторы векторов  и
и 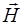 соответственно. Рассчитываются как векторное произведение набла-оператора на вектор. В декартовых координатах роторы векторов рассчитывают-ся как определители 3-го порядка:
соответственно. Рассчитываются как векторное произведение набла-оператора на вектор. В декартовых координатах роторы векторов рассчитывают-ся как определители 3-го порядка:
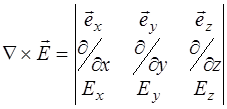 , (8.5)
, (8.5)
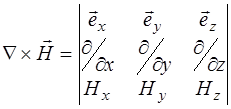 . (8.6)
. (8.6)
Подробней об уравнениях Максвелла. Первая пара урав-нений говорит о том, что электрическое поле может воз-никнуть по двум причинам. Во-первых, его источником являются электрические заряды, как сторонние так свя-занные. Во-вторых, поле  образуется всегда, когда ме-няется во времени магнитное поле (выражение закона электромагнитной индукции Фарадея).
образуется всегда, когда ме-няется во времени магнитное поле (выражение закона электромагнитной индукции Фарадея).
Вторая пара уравнений говорит о том, что магнитное поле  может возбуждаться либо движущимися электри-ческими зарядами (электрическими токами), либо пере-менными электрическими полями, либо и тем и другим одновременно. Никаких источников магнитного поля, по-добных источникам электрического поля, не существует, что следует из уравнения
может возбуждаться либо движущимися электри-ческими зарядами (электрическими токами), либо пере-менными электрическими полями, либо и тем и другим одновременно. Никаких источников магнитного поля, по-добных источникам электрического поля, не существует, что следует из уравнения 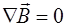 .
.
Фундаментальные уравнения Максвелла (8.1) еще не составляют полной системы уравнений электромагнитно-го поля. Этих уравнений недостаточно для нахождения полей по известным распределениям зарядов и токов. По-этому уравнения Максвелла дополняются материальными уравнениями, отражающими свойства конкретной среды.
В упрощенном виде, для медленно изменяющихся по-лей, для изотропных сред, не содержащих сегнетоэлек-триков и ферромагнетиков, материальные уравнения име-ют вид:
 , (8.7)
, (8.7)
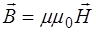 , (8.8)
, (8.8)
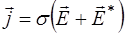 , (8.9)
, (8.9)
где 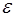 – диэлектрическая проницаемость среды;
– диэлектрическая проницаемость среды;
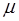 – магнитная проницаемость среды;
– магнитная проницаемость среды;
 – электропроводимость среды;
– электропроводимость среды;
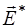 – напряженность поля сторонних сил, обусловленных химическими или тепловыми процессами.
– напряженность поля сторонних сил, обусловленных химическими или тепловыми процессами.
8.2 Уравнение электромагнитной волны
Из уравнений Максвелла следует важный вывод о су-ществовании принципиально нового физического явле-ния: электромагнитное поле может существовать само-стоятельно – без электрических зарядов и токов. При этом изменение его состояния (возмущение поля) обяза-тельно носит волновой характер. Поля такого рода назы-ваются электромагнитными волнами. Получим уравне-ния такого возмущения.
Рассмотрим однородную нейтральную непроводящую среду где выполняются материальные уравнения (8.7) – (8.9). Поскольку в данном случае плотность зарядов и токов равны нулю (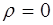 и
и 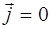 ), то уравнения Макс-велла будут иметь вид:
), то уравнения Макс-велла будут иметь вид:
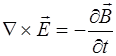 ,
,
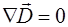 ,
,
(8.10)
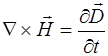 ,
,
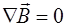 ,
,
Поскольку любые волновые процессы должны подчи-няться волновому уравнению, связывающему вторые про-изводные по времени и координатам, попытаемся прийти к нему с помощью уравнений Максвелла.
Для этого продифференцируем уравнение 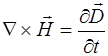 по времени и используем уравнение
по времени и используем уравнение 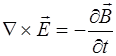 для того, чтобы связать производные по времени и по координатам в одном уравнении. Кроме того, приведем полученные уравнения к одному аргументу – вектору
для того, чтобы связать производные по времени и по координатам в одном уравнении. Кроме того, приведем полученные уравнения к одному аргументу – вектору  .
.
1. Возьмем уравнение 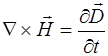 и, учтя (8.7), полу-чим:
и, учтя (8.7), полу-чим:
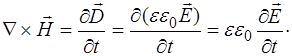 (8.11)
(8.11)
Продифференцируем полученное уравнение по врем-ени:
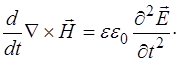 (8.12)
(8.12)
Итак, мы получили вторую частную производную по времени.
2. Получим из того же уравнения вторую частную про-изводную по направлению.Воспользовавшись тем, что мы можем менять местами операции дифференцирования, за-пишем:
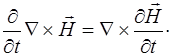 (8.13)
(8.13)
Поскольку из (8.8) следует, что:
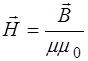 , (8.14)
, (8.14)
то (8.13) приходит к следующему виду:
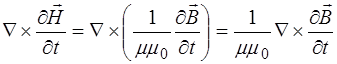 . (8.15)
. (8.15)
А поскольку 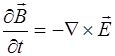 , то получаем уравнение для второй частной производной по направлению:
, то получаем уравнение для второй частной производной по направлению:
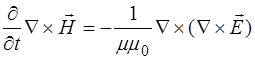 . (8.16)
. (8.16)
Итак, мы получили следующую зависимость между частными производными:
 . (8.17)
. (8.17)
Двойное векторное произведение в (8.17) преобразуем согласно правилу «бац минус цаб»:
 . (8.18)
. (8.18)
Получим:
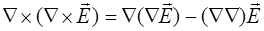 . (8.19)
. (8.19)
Поскольку дивергенция вектора напряженности элект-рического поля (по второму уравнению системы (8.10) и по уравнению(8.7)) равна нулю (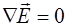 ), то окончатель-но получаем:
), то окончатель-но получаем:
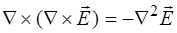 , (8.20)
, (8.20)
где 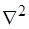 – оператор Лапласа. В декартовых координатах:
– оператор Лапласа. В декартовых координатах:
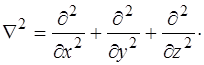
Таким образом, получаем волновое уравнение для век-тора напряженности электрического поля  :
:
 . (8.21)
. (8.21)
Аналогично можно получить и волновое уравнение для вектора напряженности магнитного поля 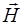 :
:
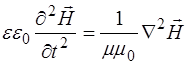 . (8.22)
. (8.22)
Итак, мы пришли к идентичным волновым уравнениям для векторов магнитной индукции  и напряженности магнитного поля
и напряженности магнитного поля 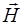 :
:
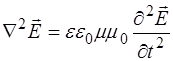 , (8.23)
, (8.23)
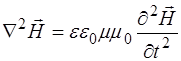 . (8.24)
. (8.24)
Исходя из сравнения полученных уравнений с общим волновым уравнением (5.79) видно, что коэффициент при вторых производных по времени есть не что иное как ве-личина, обратная квадрату скорости распространения волны. Следовательно, можно записать для скорости электромагнитной волны в веществе:
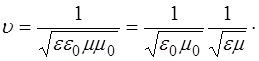 (8.25)
(8.25)
В вакууме, где 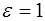 и
и 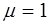 скорость волны будет рав-на скорости света в вакууме:
скорость волны будет рав-на скорости света в вакууме:
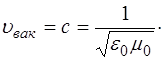 (8.26)
(8.26)
Тогда скорость волны в веществе с учетом скорости волны в вакууме будет равна:
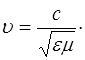 (8.27)
(8.27)
Экспериментальные данные полностью подтведили те-оретические выводы относительно совпадения скорости электромагнитной волны и скорости распространения све-та в вакууме. Это позволило Максвеллу предположить, что свет представляет собой электромагнитные волны.
8.3 Плоская электромагнитная волна
Пусть в положительном направлении оси X распрос-траняется плоская электромагнитная волна. В этом случае волновые поверхности располагаются перпендику-лярно оси X. Рассмотрим поведение вектора  на основе второго уравнения системы (8.10):
на основе второго уравнения системы (8.10):
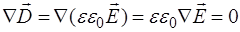 . (8.28)
. (8.28)
Разделив (8.28) на постоянные и учтя (8.3), получим:
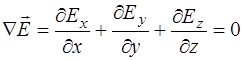 . (8.29)
. (8.29)
Поскольку волна плоская, то, если зафиксировать вол-новую поверхность в какой-то момент времени, окажется, что всех точках волновой поверхности напряженность  электрического поля постоянна, а это значит, что:
электрического поля постоянна, а это значит, что:
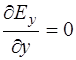 , (8.30)
, (8.30)
и
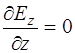 . (8.31)
. (8.31)
Оставшееся слагаемое уравнения (8.29) также равно нулю:
 , (8.32)
, (8.32)
что возможно, если проекция 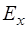 не зависит от коорди-наты. В электромагнитной волне напряженность электри-ческого поля меняется со временем, и равенство нулю производных вектора
не зависит от коорди-наты. В электромагнитной волне напряженность электри-ческого поля меняется со временем, и равенство нулю производных вектора  по осям говорит о наличии пос-тоянного электростатического поля, не связанного с рас-пространением волны, или об отсутствии такого электро-статического поля. Вектор
по осям говорит о наличии пос-тоянного электростатического поля, не связанного с рас-пространением волны, или об отсутствии такого электро-статического поля. Вектор  , связанный с прохождением электромагнитной волны, располагается перпендикуляр-но оси X, т.е. направлению распространения волны.
, связанный с прохождением электромагнитной волны, располагается перпендикуляр-но оси X, т.е. направлению распространения волны.
Проводя аналогичные рассуждения, из четвертого уравнения системы (8.10):
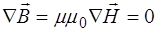 , (8.33)
, (8.33)
можно сделать вывод, что вектор напряженности магнит-ного поля 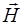 также перпендикулярен направлению рас-пространения электромагнитной волны:
также перпендикулярен направлению рас-пространения электромагнитной волны:
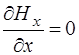 . (8.34)
. (8.34)
Таким образом, электромагнитная волна является по-перечной, что подтверждается соответствующими экспе-риментами.
Выясним, как векторы  и
и 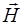 ориентированы друг от-носительно друга в электромагнитной волне. Для этого возьмем первое уравнение системы (8.10):
ориентированы друг от-носительно друга в электромагнитной волне. Для этого возьмем первое уравнение системы (8.10):
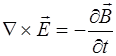 , (8.35)
, (8.35)
и представим обе его части в более удобном для анализа виде:
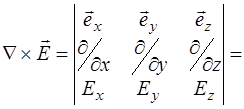
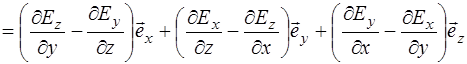 , (8.36)
, (8.36)
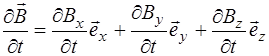 . (8.37)
. (8.37)
Из сопоставления слагаемых (8.36) и (8.37) видно, что:
 , (8.38)
, (8.38)
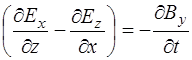 , (8.39)
, (8.39)
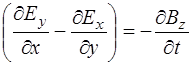 . (8.40)
. (8.40)
Таким образом, уравнение (8.35) распадается на три уравнения, которые, с учетом (8.8) могут быть представ-лены в виде:
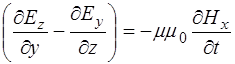 , (8.41)
, (8.41)
 , (8.42)
, (8.42)
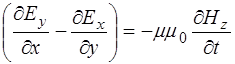 . (8.43)
. (8.43)
Поскольку изменения полей по осям Y и Z нет, то соот-ветствующие дифференциалы равны нулю, остается толь-ко изменение полей по оси X. Это позволяет упростить уравнения (8.41) – (8.43) и, с добавлением (8.32) по-лучить систему уравнений, описывающих связь между проекциями векторов напряженности электрического и магнитного полей на оси:
 |
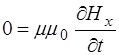 ,
,
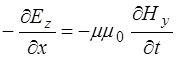 ,
,
(8.43)
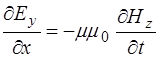 ,
,
 .
.
Проведя аналогичные рассуждения, из третьего урав-нения системы (8.10):
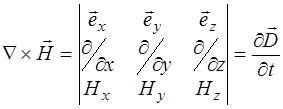 , (8.44)
, (8.44)
с добавлением уравнения (8.34) получаем следующую систему уравнений:
 ,
,
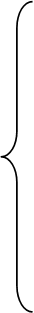
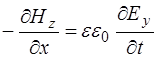 ,
,
(8.45)
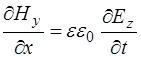 ,
,
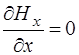 .
.
Для прояснения картины из систем (8.43) и (8.45) возьмем уравнения, содержащие проекции векторов  и
и 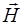 на оси
на оси  и
и 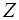 :
:
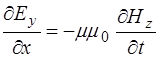 , (8.46)
, (8.46)
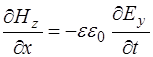 , (8.47)
, (8.47)
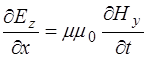 , (8.48)
, (8.48)
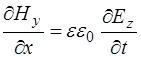 . (8.49)
. (8.49)
Уравнения (8.46) и (8.47) связывают проекции 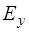 и
и  , а уравнения (8.48) и (8.49) –
, а уравнения (8.48) и (8.49) – 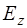 и
и 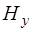 . Разберем подробней. Предположим, что первоначально было созда-но переменное электрическое поле
. Разберем подробней. Предположим, что первоначально было созда-но переменное электрическое поле 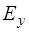 , направленное вдоль оси
, направленное вдоль оси  . Согласно уравнению (8.47) оно создаст магнитное поле
. Согласно уравнению (8.47) оно создаст магнитное поле  , направленное вдоль оси
, направленное вдоль оси 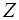 . Согласно урав-нению (8.46) поле
. Согласно урав-нению (8.46) поле  создаст электрическое поле
создаст электрическое поле 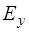 , и так далее. Ни поле
, и так далее. Ни поле 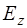 ни поле
ни поле 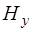 при этом не возникают.
при этом не возникают.
Аналогично, если первоначально было создано поле 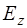 , то по уравнению (8.49) создается поле
, то по уравнению (8.49) создается поле 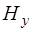 , которое, согласно уравнению (8.48) создаст поле
, которое, согласно уравнению (8.48) создаст поле 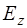 . В этом слу-чае не возникают поля
. В этом слу-чае не возникают поля 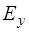 и
и  . Это означает, что век-тора
. Это означает, что век-тора  и
и 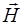 взаимно перпендикулярны.
взаимно перпендикулярны.
8.4 Связь мгновенных значений  и
и 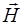
Пусть в положительном направлении оси X распрос-траняется гармоническая волна, причем вектор  колеб-лется вдоль оси Y:
колеб-лется вдоль оси Y:
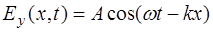 . (8.50)
. (8.50)
Найдем связь между мгновенными значениями элект-рической и магнитной компоненты электромагнитной волны. Для этого продифференцируем 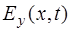 по
по 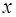 и по
и по 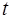 , после чего, используя уравнения (8.46) и (8.47), прост-ранственное изменение интересующих нас компонент с пространственным, а временнóе – с временным.
, после чего, используя уравнения (8.46) и (8.47), прост-ранственное изменение интересующих нас компонент с пространственным, а временнóе – с временным.
Продифференцируем (8.50) по координате 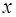 , и, учтя (8.46), запишем:
, и, учтя (8.46), запишем:
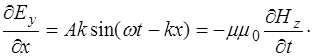 (8.51)
(8.51)
Теперь продифференцируем (8.50) по времени, и, с учетом (8.47), получим:
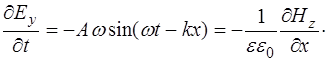 (8.52)
(8.52)
Из уравнения (8.51) с учетом связи волнового числа и скорости распространения волны (7.7), получим:
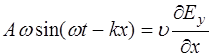 , (8.53)
, (8.53)
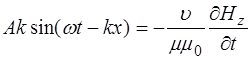 , (8.54)
, (8.54)
где 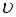 – фазовая скорость распространения волны.
– фазовая скорость распространения волны.
Из (8.52) получим:
 , (8.55)
, (8.55)
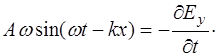 (8.56)
(8.56)
Теперь, сопоставляя уравнения (8.53) и (8.55), полу-чим связь между пространственным изменением электри-ческой и магнитной компоненты электромагнитной вол-ны:
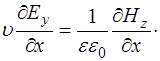 (8.57)
(8.57)
Учитывая уравнение (8.25), описывающее фазовую ско-рость распространения электромагнитной волны, после преобразований, из (8.57) получим:
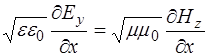 , (8.58)
, (8.58)
откуда следует, что:
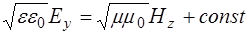 , (8.59)
, (8.59)
где произвольная постоянная обусловлена наличием пос-тоянного электрического и магнитного полей. Нас же ин-тересует только переменное поле, когда 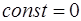 . В этом случае мы получим:
. В этом случае мы получим:
 . (8.60)
. (8.60)
Полученное выражение означает, что векторы  и
и 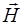 не только взаимно ортогональны, но и составляют пра-вовинтовую систему с направлением распространения (рис.8.1).
не только взаимно ортогональны, но и составляют пра-вовинтовую систему с направлением распространения (рис.8.1).
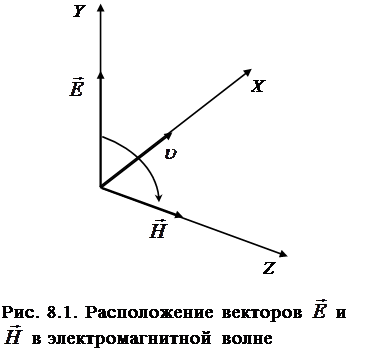 |
Поскольку векторы в электромагнитной волне пред-ставляют собой правовинтовую систему, то связь между компонентами электромагнитной волны и направлением ее распространения можно записать следующим образом (в вакууме):
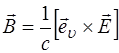 , (8.61)
, (8.61)
где 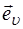 – орт направления распространения волны.
– орт направления распространения волны.
Рассмотрим, как изменяются электрическая и магнитная компонента во времени. Из уравнений (8.54) и (8.56) получим:
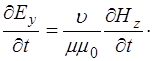 (8.62)
(8.62)
Из (8.62) видно, что  и
и 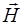 изменяются синфазно: в каждый момент времени
изменяются синфазно: в каждый момент времени 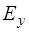 и
и  одинаковы в по знаку, одновременно превращаются в нуль и одновременно дос-тигают максимума. Вид электромагнитной волны в фик-сированный момент времени показан на рис. 8.2.
одинаковы в по знаку, одновременно превращаются в нуль и одновременно дос-тигают максимума. Вид электромагнитной волны в фик-сированный момент времени показан на рис. 8.2.
 |
| <== предыдущая | | | следующая ==> |
| Эффект Доплера для упругих волн | | | Общие сведения. Методические указания по выполнению домашнего задания |
Date: 2015-06-11; view: 629; Нарушение авторских прав