Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Методика проведения эксперимента. Задачей данной работы является ознакомление с простей-шим случаем затухающих колебаний пружинного маятника
|
|
Лабораторная работа №3
ИЗУЧЕНИЕ ТЕОРИИ ЗАТУХАЮЩИХ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА
Цель работы
Задачей данной работы является ознакомление с простей-шим случаем затухающих колебаний пружинного маятника
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ
- набор пружин и грузов
- измерительная установка для отсчета отклонений грузов
- секундомер
МЕТОДИКА ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА
 |
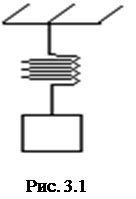Пружинный маятник – это грузик, подвешенный на пру-жине (рис. 3.1). После отклонения от положения равновесия он будет совершать вертикальные гармонические колеба-ния, если упругая пружина такова, что сила деформации пропорциональна величине удлинения пружины (
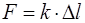, где 
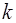– коэффициент упругости).
Колебания грузика описываются уравнением:
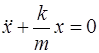. (3.1)
Это – дифференциальное уравнение собственных незату-хающих колебаний с частотой:
.
 |
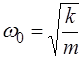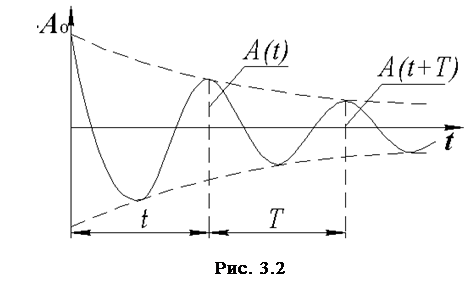Если в колеблющейся системе действуют диссипативные силы типа сил трения, пропорциональные скорости, то ко-лебания системы будут затухающими (рис. 3.2).
Уравнение колебаний будет иметь вид:
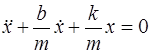, (3.2)
где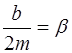 
– коэффициент затухания колебаний.
Решение дифференциального уравнения (3.2) имеет вид:
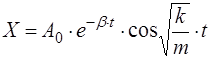. (3.3)
Из выражения (3.3) видно, что амплитуда колебаний уменьшается со временем по закону:
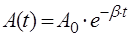. (3.4)
Период затухающих колебаний больше периода собст-венных незатухающих колебаний:
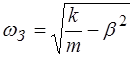, (3.5)
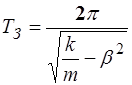. (3.6)
Затухание колебаний принято характеризовать логариф-мическим декрементом затухания:
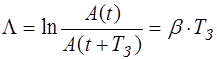. (3.7)
Учитывая, что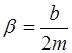 
,
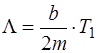. (3.8)
Пусть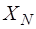 
будет отклонение, которое имеет место через время 
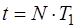, т.е. через 
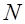колебаний после отклонения 
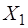. Тогда можно записать:
,
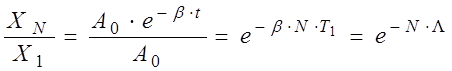откуда
,
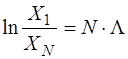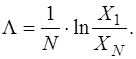(3.9)
Для пружинного маятника, колеблющегося в воздухе, ве-личина логарифмического декремента лежит в пределах от 0,01 до 0,1. Из теории затухающих колебаний следует, что вид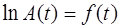 
имеет вид прямой. Здесь 
– амплитуда колебания.
Энергия колебательного движения изменяется по закону
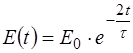, (3.10)
где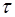 
– постоянная времени затухания (время релаксации), показывающая, что амплитуда колебания уменьшается за время 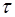в 
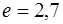раз. 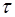– величина, обратная коэффициенту затухания 
.
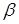Из (3.10) видно, что энергия осциллятора расходуется на работу против диссипативных сил и превращается во внут-реннюю энергию.
Мощность потерь, т.е. скорость рассеяния энергии, с од-ной стороны,
,
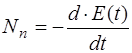а с другой, с учетом (3.10),
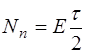. (3.11)
Качество колебательной системы, ее способность сохра-нять запасенную энергию характеризуется добротностью Q, которая определяется отношением запасенной энергии к потерям за время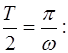 
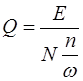. (3.12)
C учетом (3.11) выражение для добротности принимает вид:
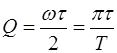. (3.13)
Из (3.13) следует, что добротность колебательной сис-темы равна числу колебаний за время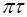 
; причем за это время амплитуда уменьшается в 
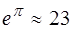раза, а энергия в 
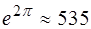раз.
Date: 2015-06-11; view: 348; Нарушение авторских прав