Формирование процесса восстановления

Далее рассмотрим работу восстанавливаемого изделия. Для этого в качестве исходных данных используем как наработку до первого, так и до второго отказа. Так как автомобиль является восстанавливаемым изделием, то после устранения 1-го отказа автомобиль продолжает работу, и по той же схеме возникают и устраняются 2-й, 3-й и последующие отказы. По результатам расчетов строим схему формирования процесса восстановления (рисунок 5.9) используя данные f₁(L) (таблица 5.3) и f₂(L) (таблица 5.4).

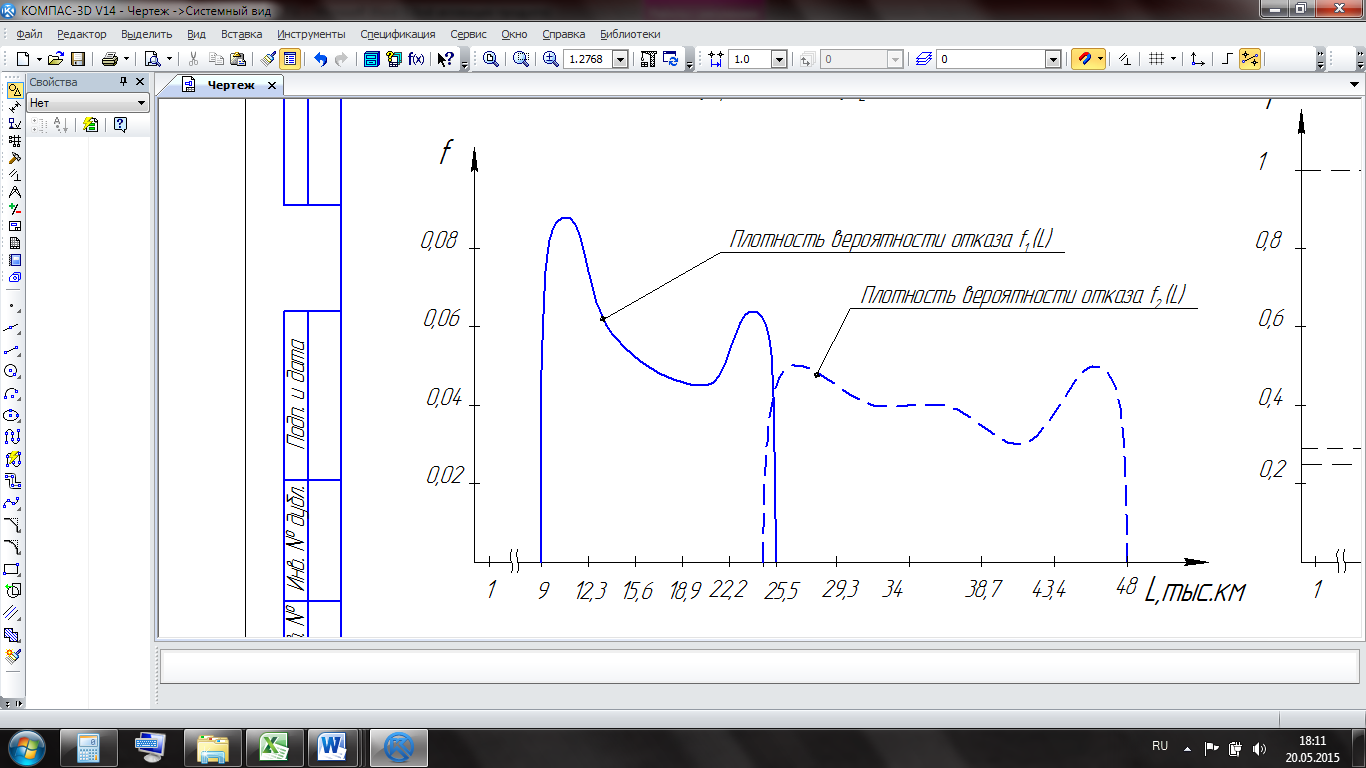
Рисунок 9 – Схема формирования процесса восстановления

Закономерности изменения потока отказов описывают изменение по наработке показателей, характеризующих процесс возникновения и устранения отказов автомобилей.

Очевидно, что наработки на отказы, во-первых, случайны для каждого автомобиля и описываются соответствующей функцией f(L), во-вторых, эти наработки независимы для разных автомобилей, в третьих, при устранении отказа в зоне ремонта безразлично, какой автомобиль отказал или какой отказ по счету.

К важнейшим характеристикам этих закономерностей относятся средняя наработка до k-го отказа L_k, средняя наработка между отказами для n изделий L_k,k+1, коэффициент полноты восстановления ресурса h, ведущая функция потока отказов W(L) и параметр потока отказов w(L).

Средняя наработка до k-го отказа:

(5.15)

гдеL₁ – средняя наработка до первого отказа;

L₁₂ – средняя наработка между первым и вторым отказом.

Средняя наработка между (k-1)-м и k-м отказами для n автомобилей:

(5.16)

Коэффициент полноты восстановления ресурса характеризует возможность сокращения ресурса после ремонта:

(5.17)

Сокращение ресурса после первого и последующего ремонтов, которое необходимо учитывать при планировании и организации работ по обеспечению работоспособности объясняется: частичной заменой только отказавших деталей, при значительном сокращении надежности других, особенно сопряженных; использованием в ряде случаев запасных частей и материалов худшего качества, чем при изготовлении автомобиля; низким технологическим уровнем работ.

Используя исходные данные примера расчета, определяем среднюю наработку до k-го отказа и коэффициент полноты восстановления ресурса:

(тыс.км).

.

1

Ведущая функция потока отказов (функция восстановления) определяет накопленное количество первых и последующих отказов изделия к наработке L. В курсовой работе определяем данную функцию по трем любым наработкам (рисунок 5.10), лежащих в интервале от средней наработки до первого отказа, до средней наработки до второго отказа. Из-за вариации наработок на отказы происходит смешение отказов, а функции вероятностей 1-го и 2-го отказов F₁(L) и F₂(L) частично накладываются друг на друга.

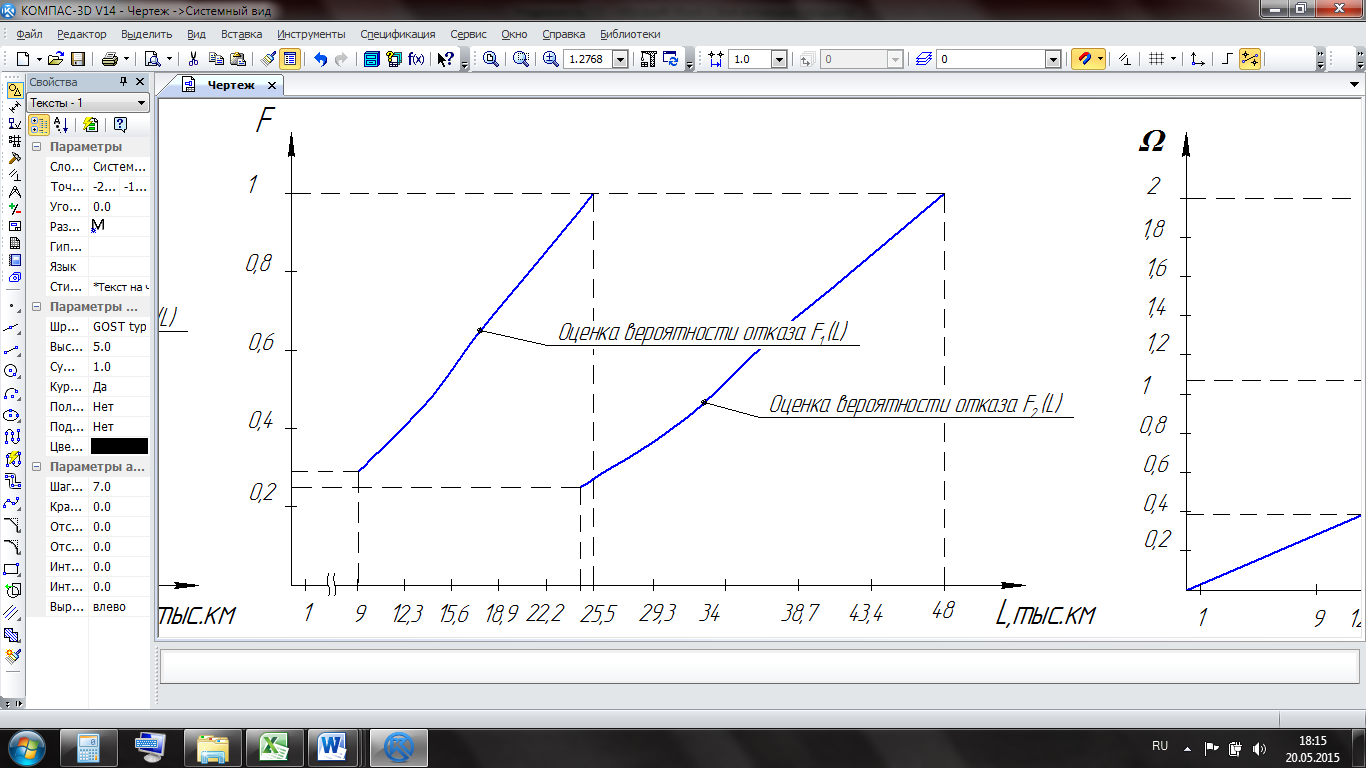
Рисунок 5.10 – Формирование ведущей функции

Рисунок 5.11 – Формирование ведущей функции

В общем виде ведущая функция потока отказов:

(5.18)

Для каждого частного случая:

L₁: W(L₁)=F₁(L₁) – произошел только 1-й отказ.

L₂: W(L₂)=F₁(L₂)+ F₂(L₂) – произошел 1-й и 2-й отказ.

L₃: W(L₃)=F₁(L₃)+ F₂(L₃) – произошел 1-й и 2-й отказ.

Процесс формирования ведущей функции восстановления представлен на рисунке 10.

Для практического расчета W(L) необходимо собрать данные о вероятности первого, второго и т.д. отказов и просуммировать их.

Параметр потока отказов w(L) – это плотность вероятности возникновения отказа восстанавливаемого изделия, определяемая для данного момента времени или пробега

(5.19)

Иными словами w(L) – это относительное число отказов, приходящееся на единицу времени или пробега одного изделия. Следует отметить, что ведущая функция и параметр потока отказов определяется аналитически как функции параметров этих законов лишь для некоторых видов законов распределения. Наиболее часто встречаются нормальный, логарифмически нормальный, Вейбулла-Гнеденко и экспоненциальный.

Например, для экспоненциального закона:

. (5.20)

Откуда следует, что:

. (5.21)

Для нормального закона:

(5.22)

где Ф – нормированная функция для ;

k – число отказов.

. (5.23)

В рассматриваемом нами примере курсовой работы средняя наработка до первой замены изделия равна 16,521 тыс. км, среднеквадратическое отклонение равно 5,043 тыс. км, а коэффициент полноты восстановления ресурса составляет 1,1. Необходимо определить возможное число замен при произвольно взятом пробеге в интервале между средними наработками до первого и второго отказа автомобиля. В интервале от 17 до 36 тыс. км, произвольно выберем пробег равный 27 тыс.км.

Определим F₁, F₂, F₃:

;

;

.

Ввиду того, что F₂ и F₃ мало, последующие расчеты для F₄ и других можно не производить. Таким образом, к пробегу 27 тыс. км возможное число замен данной детали составит:

Для практического использования важны некоторые приближенные оценки ведущей функции параметра потока отказов

(5.24)

Из этой формулу следует, что на начальном участке работы, где преобладают первые отказы, т.е. F(L) ≤ 1, W(L)»F(t).

Ведущая функция параметра потока отказов стареющих элементов для любого момента времени удовлетворяет следующему неравенству:

(5.25)

Для рассмотренного выше примера получим следующую оценку ведущей функции параметра потока отказов при пробеге автомобиля L = 27 тыс. км: по точным расчетам эта величина составляет 1 отказ.

Date: 2015-07-17; view: 722; Нарушение авторских прав