
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Разработка алгоритма поиска отказа
|
|
Для составления алгоритма поиска отказа, близкого к оптимальному, необходимо использовать методы теории информации, где в качестве ведущей функции используется количество информации, содержащееся в проверке.
Каждая проверка содержит некоторое количество информации о состоянии системы:
IПj = H(S)-H(S/Пj), (4.1)
где H(S) – полная неопределенность техсостояния системы; H(S/Пj) - оставшаяся неопределенность состояния системы после выполнения элементарной проверки.
На практике для расчёта используем формулу:
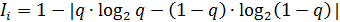 , (4.2)
, (4.2)
где q – определяется на основе статистических данных о надёжности элементов системы.
Вероятности состояний S1, S2,.. Sn выбираются из следующих условий: наиболее ответственные элементы, такие как тормозной крап, компрессор, регулятор давления, тормозные камеры, главный и рабочие тормозные цилиндры (для тормозных систем), радиатор, водяной насос, термостат (для систем охлаждения), карбюратор, бензонасос, фильтры, подкачивающий насос и насос высокого давления (для систем питания), аккумулятор, катушка зажигания, прерыватель-распределитель (для систем зажигания) имеют значительную вероятность – 0,1...0,25. Каждая форсунка и свеча зажигания – 0,05...0,1. Вероятности остальных состояний принимаются одинаковыми по выражению:
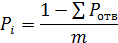
где 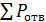 – сумма вероятностей отказов основных элементов; m – количество оставшихся состояний (отказов).
– сумма вероятностей отказов основных элементов; m – количество оставшихся состояний (отказов).
Вероятность безотказной работы:
q=∑(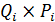 )
)
Таким образом имеем: P1 = 0,05; P2 = 0,15; P3 = 0,2; P4 = 0,2; P5-8 = 0,1.
Таблица 4.1 – Таблица состояний и известной информативностью
| e | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 | q | I | |
| z1 | 0,95 | 0,85 | |||||||||
| z2 | 0,8 | 0,79 | |||||||||
| z3 | 0,5 | 1,0 | |||||||||
| z4 | 0,4 | 0,91 | |||||||||
| z5 | 0,3 | 0,84 | |||||||||
| z6 | 0,2 | 0,79 | |||||||||
| z7 | 0,1 | 0,8 | |||||||||
| z8 | - |
Поиск отказа начинается с проверки, несущей наибольшее количество информации. Наибольшую информацию имеет проверка, проверяющая mэлементов с суммарной вероятностью различаемых отказов, равной 0,55. В нашем случае это строка z3.
После проведения проверки, при которой контролируется т блоков системы, могут быть два случая:
а) отказ фиксируется. Тогда он содержится в каком-нибудь из элементов i= 1…m,
б) отказ не фиксируется.
Далее рассматриваются две таблицы: первая включает в себя столбцы, в которых были нули при проведении первой проверки и все проверки (строки), вторая включает столбцы, в которых были единицы и все строки (проверки).
По каждой из таблиц выбирается проверка по тем же правилам. Суммарная вероятность выявляемых отказов должна быть наиболее близка к 0,5. Они в свою очередь, тоже будут разбивать уже эти столбцы на два подмножества (где в строках нули и где единицы) и т.д.
Процедура повторяется до отыскания отказов всех элементов.
Запишем ветку дерева отказов при z3 (R=0).
Таблица 4.2 а – Таблица, включающая значения «0»
| Q1 | Q2 | Q3 | q | I | |
| z1 | 0,35 | 0,87 | |||
| z2 | 0,2 | 0,79 |
При z1 (R=0) Q1.
Таблица 4.2 б – Таблица, включающая значения «1»
| Q4 | Q5 | Q6 | Q7 | Q8 | q | I | |
| z4 | 0,4 | 0,91 | |||||
| z5 | 0,3 | 0,84 | |||||
| z6 | 0,2 | 0,79 | |||||
| z7 | 0,1 | 0,8 | |||||
| z8 | - |
При z4 (R=0) Q4,
Таблица 4.3 а – Таблица, включающая значения «0»
| Q2 | Q3 | |
| z2 |
При z2 (R=0) Q2, при z2 (R=1) Q3
Таблица 4.3 б – Таблица, включающая значения «1»
| Q5 | Q6 | Q7 | Q8 | q | I | |
| z5 | 0,3 | 0,84 | ||||
| Z6 | 0,2 | 0,79 | ||||
| Z7 | 0,1 | 0,8 | ||||
| Z8 | - |
При z5 (R=0) Q5,
Таблица 4.4 – Таблица, включающая значения «1»
| Q6 | Q7 | Q8 | q | I | ||
| Z6 | 0,2 | 0,79 | ||||
| Z7 | 0,1 | 0,8 | ||||
| Z8 | - | |||||
При z7 (R=1) z6,
Таблица 4.5 – Таблица, включающая значения «1»
| Q6 | Q7 | |
| Z6 |
При z6 (R=1) Q6, При z6 (R=0) Q8,
В итоге выполнив все проверки, выполняем построение дерева отказов.
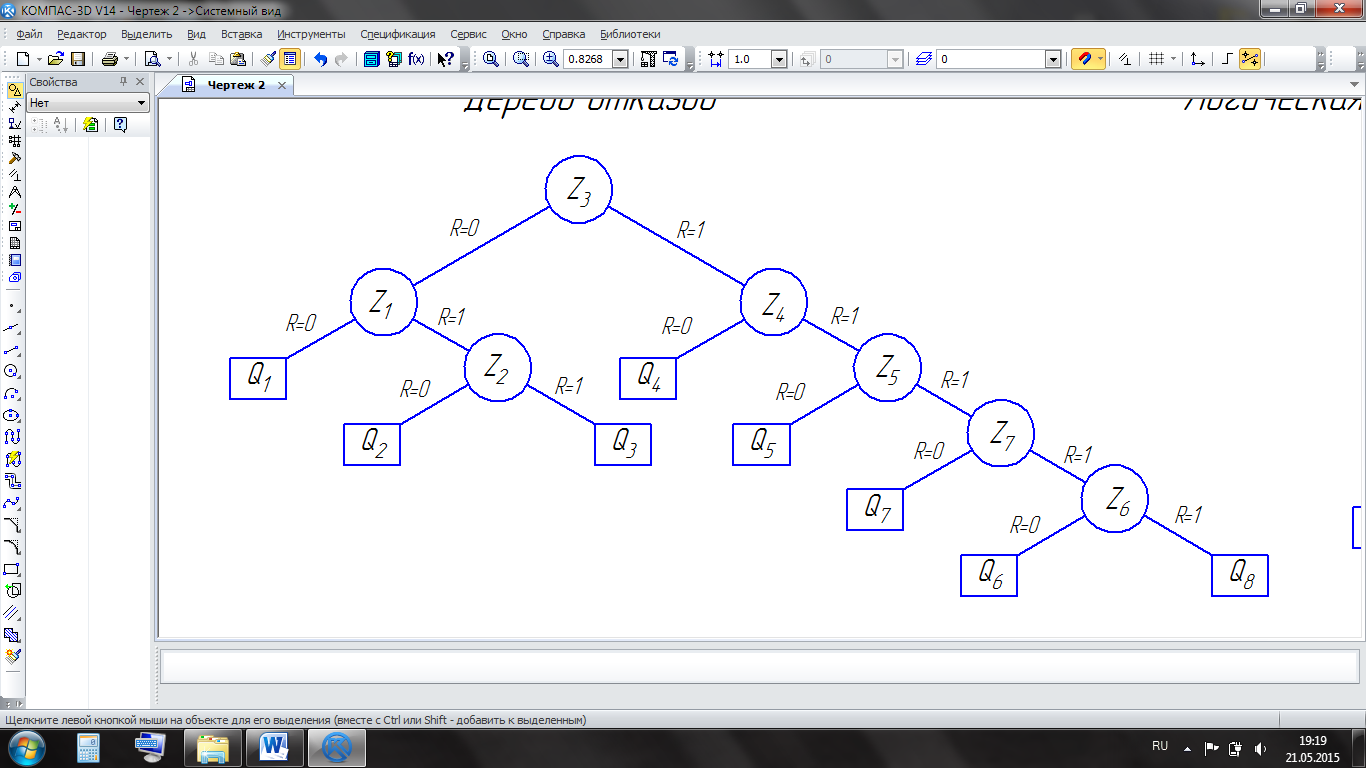
Рисунок 4.1 – Дерево отказов
5. Расчёт характеристик надёжности и безотказности изделия
Исходными данными расчета основной части курсовой работы являются:
Наработка до первого отказа (таблица 5.1):
Таблица 5.1 – Наработка до первого отказа
| 15,7 | 17,6 | 15,8 | 23,6 | 12,4 | 13,2 | 24,7 | 11,3 | 19,6 |
| 10,2 | 9,6 | 16,1 | 20,9 | 16,1 | 20,4 | 25,5 | ||
| 20,6 | 11,9 | 24,2 | 18,4 | 12,5 | 11,4 | 10,5 | 10,2 | 18,9 |
| 21,1 | 10,2 | 17,3 | 9,4 | 9,1 | 19,1 | 11,8 | 23,4 | 10,8 |
| 22,5 | 13,6 | 14,2 | 10,2 | 17,5 | 14,3 | |||
| 18,7 | 22,4 | 9,1 | 10,2 | 10,7 | 13,9 | 10,4 | ||
| 12,2 | 22,2 | 10,5 | 13,1 | 15,2 | 23,4 | 21,3 | 15,9 | |
| 21,1 | 11,3 | 24,8 | 22,8 | 22,6 | 17,2 | 17,2 | 18,1 | |
| 25,4 | 19,1 | 18,8 | 15,2 | 11,4 | 14,8 | 13,5 | ||
| 22,9 | 12,8 | 22,6 | 10,6 | 20,7 | 22,7 |
Наработка до второго отказа (таблица 5.2):
Таблица 5.2 – Наработка до второго отказа
| 40,5 | 29,7 | 31,6 | 33,5 | 43,3 | 27,2 | 46,9 | 29,3 | 44,6 |
| 42,1 | 38,7 | 47,6 | 30,8 | 47,1 | 28,9 | |||
| 27,4 | 36,4 | 47,1 | 44,4 | 39,7 | 29,6 | 31,1 | ||
| 25,5 | 38,8 | 42,1 | 26,1 | 44,9 | 39,2 | |||
| 37,7 | 39,1 | 34,2 | 38,1 | 25,4 | 31,5 | 26,5 | 44,8 | 46,3 |
| 25,8 | 29,4 | 31,6 | 35,6 | 28,8 | 34,4 | 26,3 | 41,9 | 46,6 |
| 45,9 | 38,6 | 32,7 | 39,8 | 36,3 | 35,3 | 41,6 | 33,8 | 36,4 |
| 33,2 | 24,9 | 46,3 | 47,7 | 33,4 | 24,6 | 35,1 | 44,3 | |
| 27,8 | 45,2 | 35,3 | 46,2 | 26,2 | 27,5 | 42,3 | 26,3 | |
| 33,6 | 47,2 | 25,2 | 41,6 | 45,8 | 38,4 | 46,2 | 28,5 | 31,7 |
Для любого случайно выбранного изделия невозможно заранее определить, будет ли оно надежно. Из двух двигателей одной марки в одном могут вскоре возникнуть отказы, а второй будет исправным длительное время.
Отказ – событие случайное. Поэтому для расчета показателей надежности используют методы теории вероятностей и математической статистики. Одним из условных понятий, используемых при расчетах показателей надежности, является ²наработка².
Наработкой называется продолжительность или объем работы изделия. Для двигателей наработку обычно измеряют в километрах пробега автомобиля или в моточасах. В технической и учебной литературе можно встретить такие выражения: суточная наработка, наработка до первого отказа, наработка между отказами и т.д. Обычно применяется следующая буквенная индексация рассматриваемых далее в курсовой работе событий и понятий:
- «F»(failure) – отказ, авария, повреждение, вероятность этих событий;
- «R»(reliability) – безотказность, надежность, прочность, вероятность этих событий;
- «Р»(probability) – вероятность.
Рассмотрим простейшие методы оценки случайных величин. Исходные данные (таблицы 1 и 2) – результаты наблюдений за изделиями или отчетные данные, которые выявили индивидуальные реализации случайных величин (наработки на отказ). Для расчета вероятности отказа и безотказной работы агрегата или автомобиля, а также для определения плотности вероятности отказа (закон распределения случайной величины) условно принимаем изделия как невосстанавливаемые, то есть, исследуем наработку изделия до первого «условно единственного» отказа.
5.1 Расчёт характеристик случайных величин до первого отказа
Сначала проводим расчёты наработок до первого отказа. Далее необходимо произвести точечные оценки случайных величин.
Среднее значение случайных величин определяем по формуле (1):
 (5.1)
(5.1)
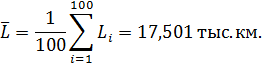
Размах случайных величин определяем по формуле (2):
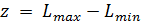 (5.2)
(5.2)

Дисперсию рассчитаем по формуле (3):
 (5.3)
(5.3)
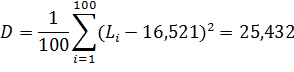
Среднеквадратическое отклонение s найдём как квадратный корень значения дисперсии по формуле (4):
 (5.4)
(5.4)

Коэффициент вариации v считаем по формуле (5):
 (5.5)
(5.5)
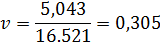
Точечные оценки позволяют нам предварительно судить о качестве изделий и технологических процессов. Чем ниже средний ресурс и выше вариация (s, v, z), тем ниже качество конструкции и изготовления (или ремонта) изделия. Чем выше коэффициент вариации показателей технологических процессов ТЭА (трудоемкость, простои в ТО или ремонте, загрузка постов и исполнителей и др.), тем менее совершенны применяемые организация и технология ТО и ремонта.
Далее рассчитываем вероятностные оценки случайных величин. При выполнении расчётов для составления сводной таблицы необходимо разбить размах случайных величин на 5 равных по длине интервалов (таблица 5.3). Далее проведём группировку, т.е. определим число случайных величин, попавших в первый (n1), второй (n2) и остальные интервалы. Это число называется частотой. Разделив каждую частоту на общее число случайных величин (n1 + n2 +... + nп=n), определим частотность, которая рассчитывается по формуле (6):
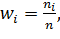 (5.6)
(5.6)
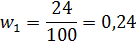
Частотность является эмпирической оценкой вероятности Р, т.е. при увеличении числа наблюдений частотность приближается к вероятности: wi→pi.
Полученные при группировке случайных величин результаты сводятся в таблицу 5.3, данные которой имеют не только теоретическое, но и практическое значение, т.е. имея систематизированные данные по отказам, можно прогнозировать и планировать число воздействий (программу работ), потребности в рабочей силе, площадях, материалах и запасных частях.
F(L) называют интегральной функцией распределения, f(L) – дифференциальной функцией распределения.
Имея значения F(x) или f(x), можно произвести оценку надежности и определить среднюю наработку до отказа:
 . (5.7)
. (5.7)
При оценке качества изделий, нормировании ресурсов, в системе гарантийного обслуживания применяют гамма – процентный ресурс ху. Это интегральное значение ресурса ху, которое вырабатывает без отказа не менее г процентов всех оцениваемых изделий, т.е:
 (5.8)
(5.8)
В ТЭА обычно принимаются γ = 80, 85, 90 и 95%. Примем γ = 80%. Гамма – процентный ресурс используется при определении периодичности ТО по заданному уровню безотказности. Выражение LTO = Lγ означает, что обслуживание с периодичностью LTO гарантирует вероятность безотказной работы R ≥ γ и отказа F ≤ (1 – γ).
Для первых отказов невосстанавливаемых изделий и взаимно дополняющих событий (отказ – работоспособное состояние) имеет место условие F(L) + R(L) = 1, т.е., зная вероятность отказа, можно определить вероятность безотказной работы и наоборот.
Важным показателем надежности является интенсивность отказов l (L) – условная плотность вероятности возникновения отказа невосстанавливаемого изделия, определяемая для данного момента времени при условии, что отказа до этого момента не было. Аналитически для получения l(L) необходимо элементарную вероятность dm/dL отнести к числу элементов, не отказавших к моменту L, т.е.
 (5.9)
(5.9)
Так как вероятность безотказной работы R(L) = [n – m(L)]/n,то:
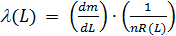 . (5.10)
. (5.10)
Учитывая, что f(L)=(1/n)(dm/dL), получаем:
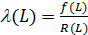 , (5.11)
, (5.11)
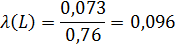
Далее производим расчёт вероятности случайного события. В общем виде, вероятность случайного события – это отношение числа случаев, благоприятствующих данному событию, к общему числу случаев.
Вероятность отказа рассматривается за определенную наработку L:

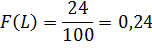
где m(L) – число отказов за L(тыс.км); n – число наблюдений (изделий).
Вероятность отказа изделия при наработке L равна вероятности событий, при которых наработка до отказа конкретных изделий Li окажется менее L.
Отказ и безотказность являются противоположными событиями, поэтому:
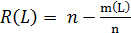 , (5.13)
, (5.13)
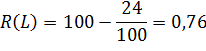
где  – число изделий, не отказавших за L.
– число изделий, не отказавших за L.
Следующей характеристикой случайной величины является плотность вероятности (например, вероятности отказа) f(L) – функция, характеризующая вероятность отказа за малую единицу времени при работе узла, агрегата, детали без замены. Если вероятность отказа за наработку равна 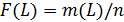 , то, дифференцируя ее при
, то, дифференцируя ее при 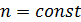 , получим плотность вероятности отказа
, получим плотность вероятности отказа
 (5.14)
(5.14)
где 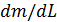 – элементарная "скорость", с которой в любой момент времени происходит приращение числа отказов при работе детали, агрегата без замены.
– элементарная "скорость", с которой в любой момент времени происходит приращение числа отказов при работе детали, агрегата без замены.
Результаты проведённых расчётов заносим в таблицу 5.3
Таблица 5.3 – Результаты расчётов
| Определяемая величина | Номер интервала отказа | ||||||
| Границы интервала наработки (первый отказ), тыс. км. | ΔL | 9-12,3 | 12,3-15,6 | 15,6-18,9 | 18,9-22,2 | 22,2-25,5 | |
| Значение середины интервала, тыс. км | Li | 10,65 | 13,95 | 17,25 | 20,55 | 23,85 | |
| Число отказов в интервале | ni | ||||||
| Число отказов к моменту наработки Li | m(L) | ||||||
| Число работоспособных объектов к моменту наработки xi | n - m(L) | ||||||
| Частость (вероятность) | wi = ni / n | 0,29 | 0,19 | 0,16 | 0,15 | 0,21 | |
| Оценка накопленных вероятностей отказа | F1(L) = m(L)/n | 0,29 | 0,48 | 0,64 | 0,79 | ||
| Оценка накопленных вероятностей безотказности | R1(L) = n-m(L)/n | 0,71 | 0,52 | 0,36 | 0,21 | ||
| Плотность вероятности отказа | f1(L)= ni /ΔL/ n | 0,088 | 0,058 | 0,048 | 0,045 | 0,064 | |
| Плотность вероятности возникновения отказа | λ(L)=f1(L)/R1(L) | 0,124 | 0,111 | 0,135 | 0,216 | - |
Среднее значение случайной величины, рассчитанное по формуле (5.1) равно:
 тыс.км.
тыс.км.
Размах случайной величины, рассчитанный по формуле (5.2), равен:
z = 22,5 – 9 = 16,5 (тыс.км).
Количество интервалов случайных величин принимаем равнымn = 5.
Шаг интервала принимаем равным:
S = 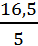 = 3,3 (тыс.км).
= 3,3 (тыс.км).
Дисперсия, рассчитанная по формуле (5.3), равна:
D= 25,432.
Среднеквадратическое отклонение случайной величины, рассчитанное по формуле (5.4), равно:
 .
.
Коэффициент вариации, рассчитанный по формуле (5.5), равен:
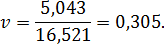
Полигон распределения, построенный по данным таблицы 5.3, изображён на рисунке 5.4.
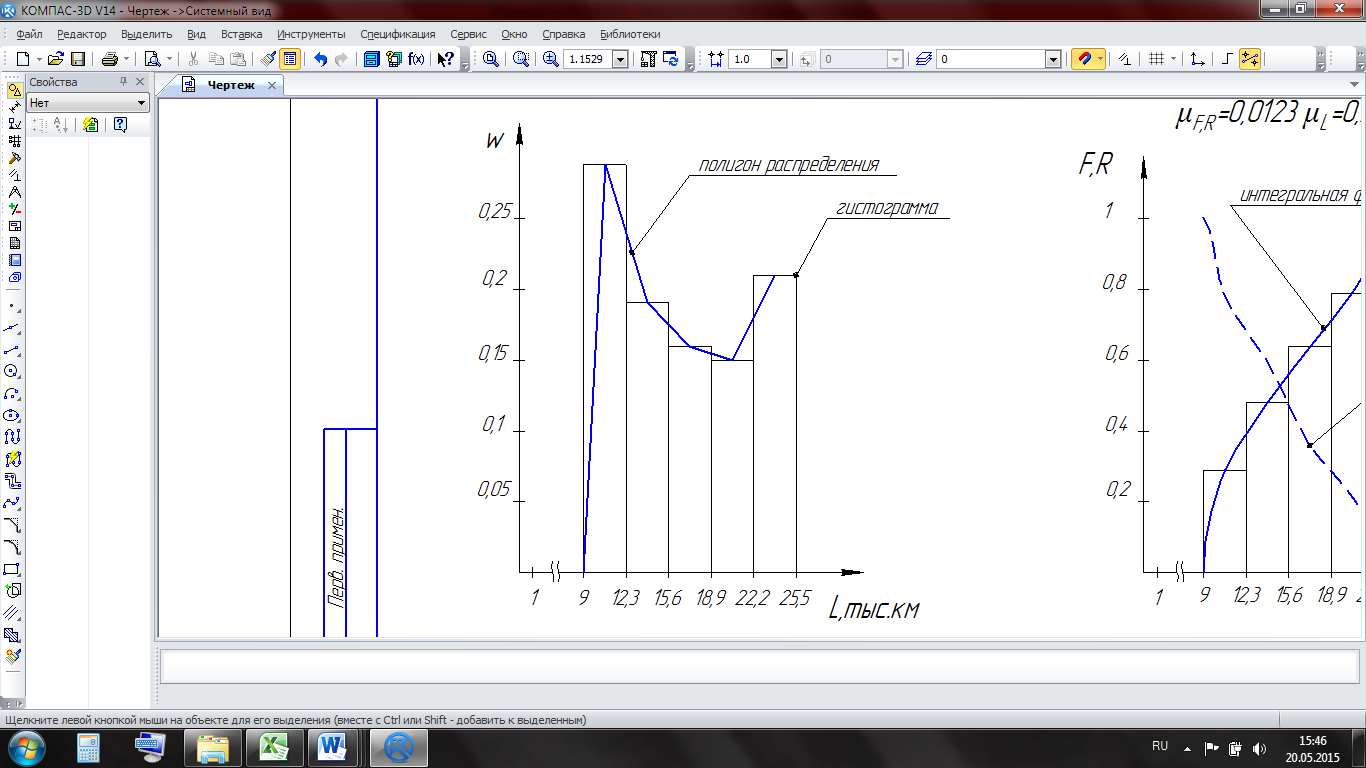
Рисунок 5.1 – Графическое изображение случайной величины
Наглядное представление о случайных величинах дает их графическое изображение интегральных функции распределения вероятностей отказа и безотказной работы (рисунок 5.2).
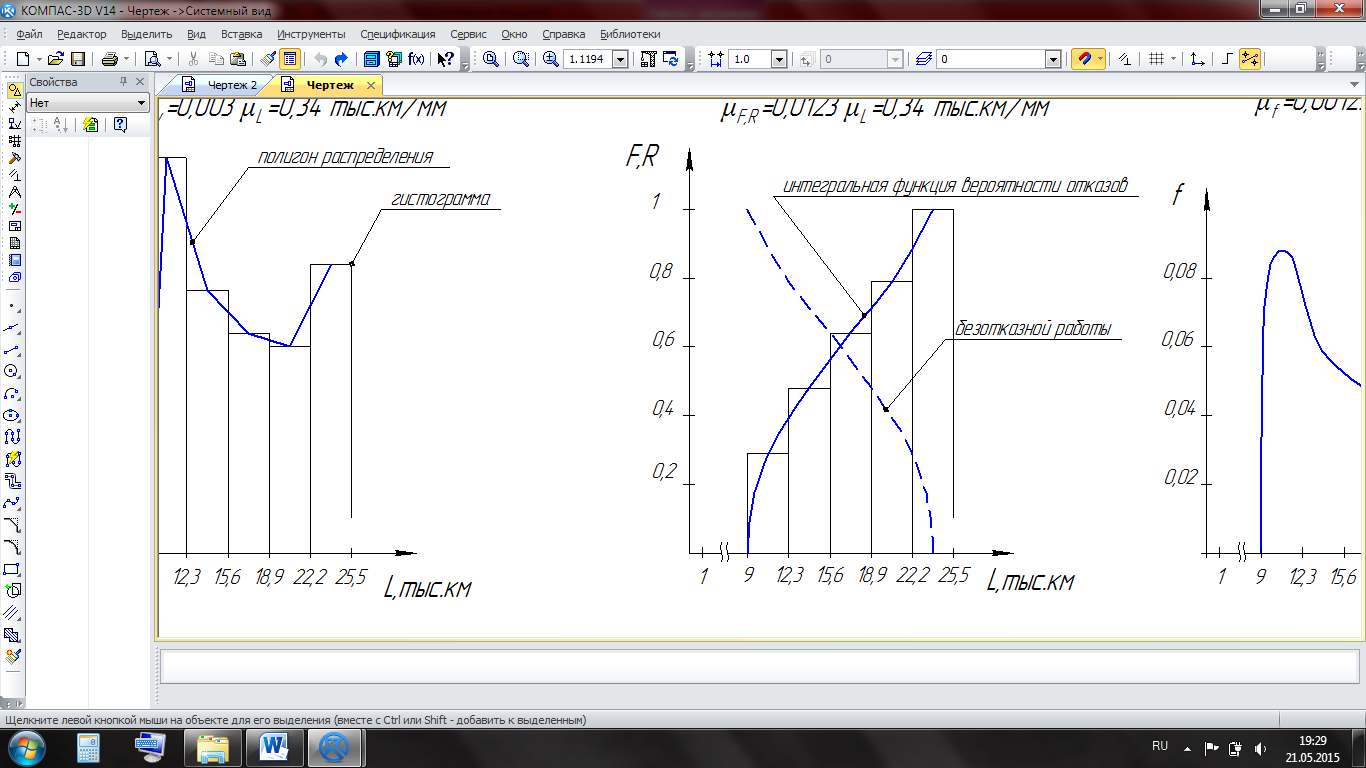
Рисунок 5.2 – Графическое изображение случайной величины
Наглядное представление о вариации случайной величины дает графическое изображение дифференциальной функции или закона распределения случайной величины (рисунок 5.3).
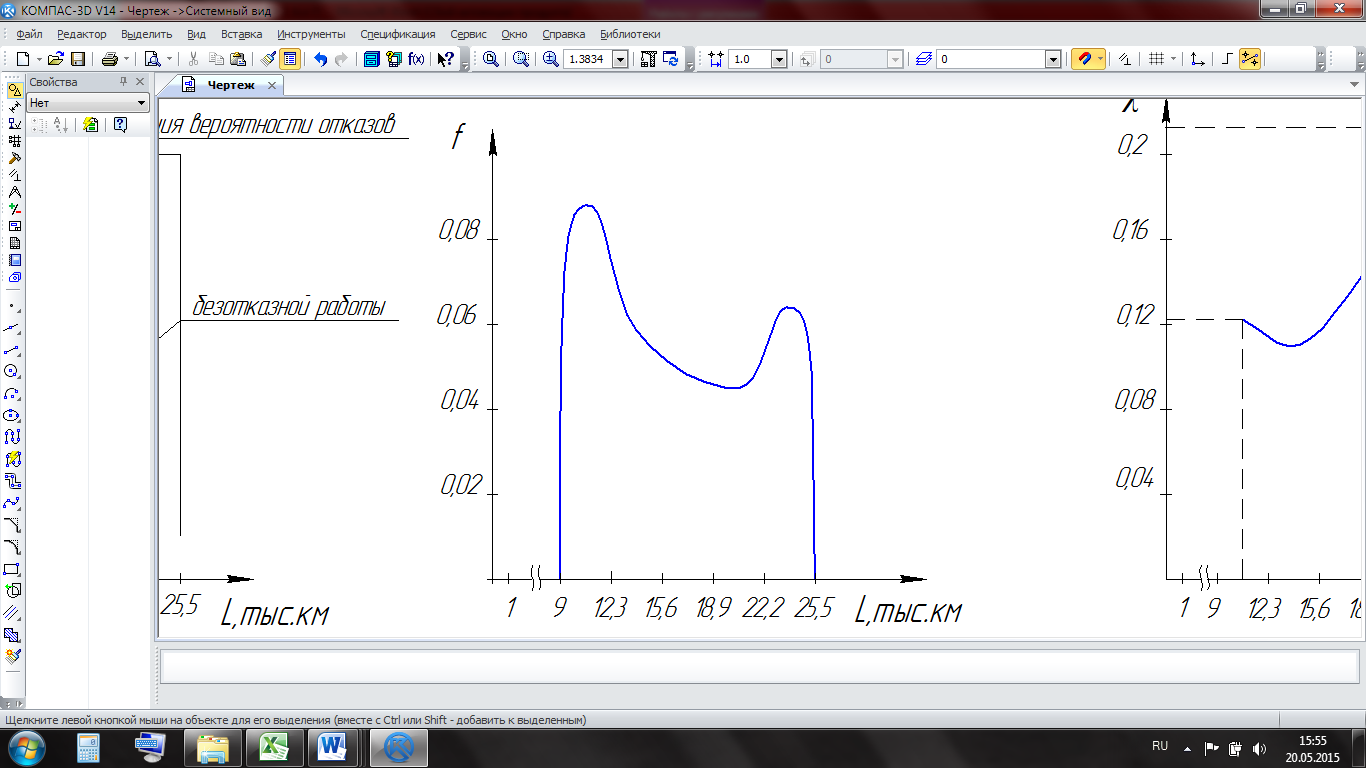
Рисунок 5.3 – Дифференциальная функция распределения
Наглядное представление о величине изменения интенсивности отказов l(L) реализуется в виде графика (рисунок 5.4).
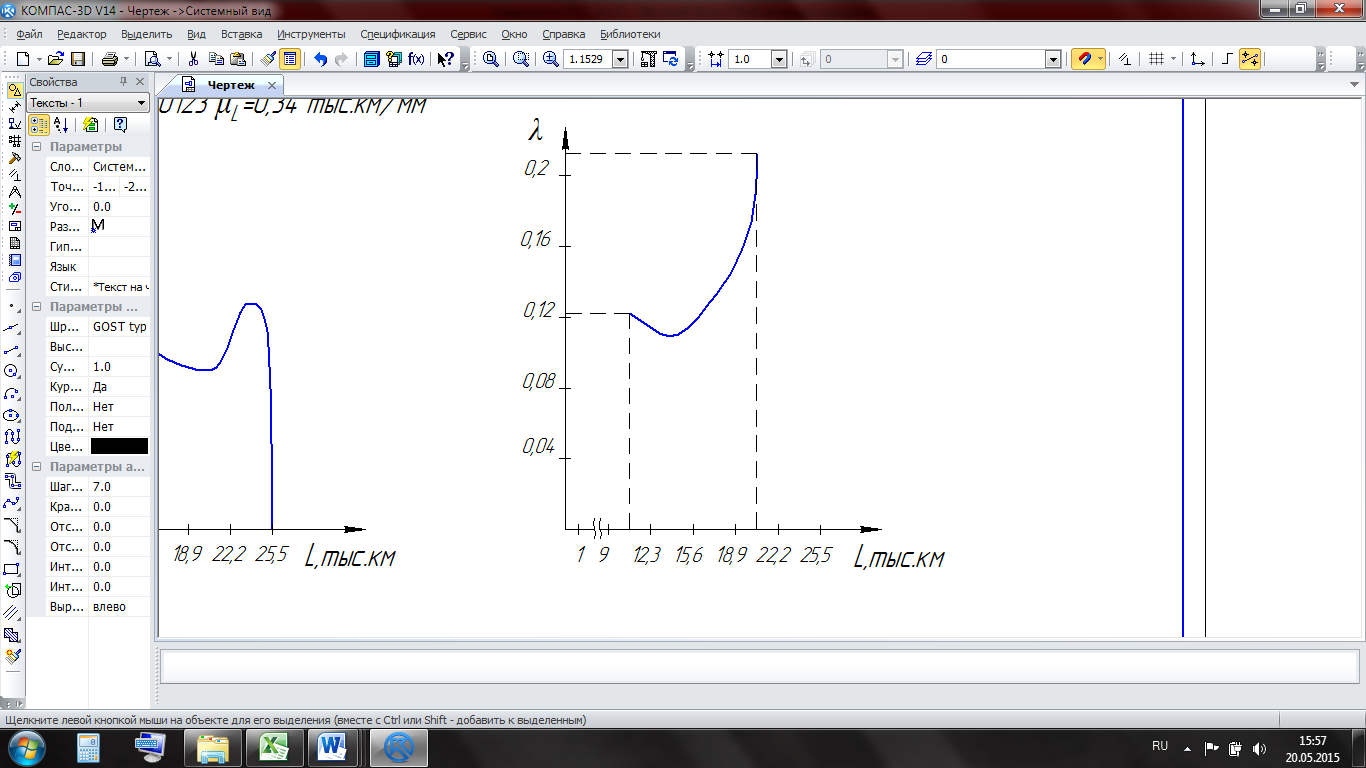
Рисунок 5.4 – Изменение интенсивности отказов
5.2 Расчёт характеристик случайных величин до второго отказа
Аналогично расчётам случайных величин до первого отказа, проводим расчёты случайных величин до второго отказа и полученные результаты заносим в таблицу 5.4.
Таблица 5.4 – Результаты расчётов
| Определяемая величина | Номер интервала отказа | |||||
| Границы интервала наработки (первый отказ), тыс. км. | ΔL | 24,6-29,3 | 29,3-34 | 34-38,7 | 38,7-43,4 | 43,4-48 |
| Значение середины интервала, тыс. км | Li | 26,45 | 31,15 | 35,85 | 40,55 | 45,25 |
| Число отказов в интервале | Ni | |||||
| Число отказов к моменту наработки Li | m(L) | |||||
| Число работоспособных объектов к моменту наработки xi | n - m(L) | |||||
| Частость (вероятность) | wi = ni / n | 0,25 | 0,19 | 0,18 | 0,16 | 0,22 |
| Оценка накопленных вероятностей отказа | F2(L) = m(L)/n | 0,25 | 0,44 | 0,62 | 0,78 | |
| Оценка накопленных вероятностей безотказности | R2(L) = n-m(L)/n | 0,75 | 0,56 | 0,38 | 0,22 | |
| Плотность вероятности отказа | f2(L)= ni /ΔL/ n | 0,05 | 0,04 | 0,04 | 0,03 | 0,05 |
| Плотность вероятности возникновения отказа | λ(L)=f2(L)/R2(L) | 0,07 | 0,07 | 0,10 | 0,16 | - |
реднее значение случайной величины, рассчитанное по формуле (5.1) равно:
 тыс.км.
тыс.км.
Размах случайной величины, рассчитанный по формуле (5.2), равен:
Z= 48 – 24,6 = 23,4 (тыс.км).
Количество интервалов случайных величин принимаем равнымn = 5.
Шаг интервала принимаем равным:
S = 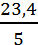 = 4,68 (тыс.км).
= 4,68 (тыс.км).
Дисперсия, рассчитанная по формуле (5.3), равна:
D= 52,8.
Среднеквадратическое отклонение случайной величины, рассчитанное по формуле (5.4), равно:

Коэффициент вариации, рассчитанный по формуле (5.5), равен:
v = 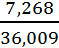 = 0,2
= 0,2
Полигон распределения, построенный по данным таблицы 5.3, изображён на рисунке 5.4.
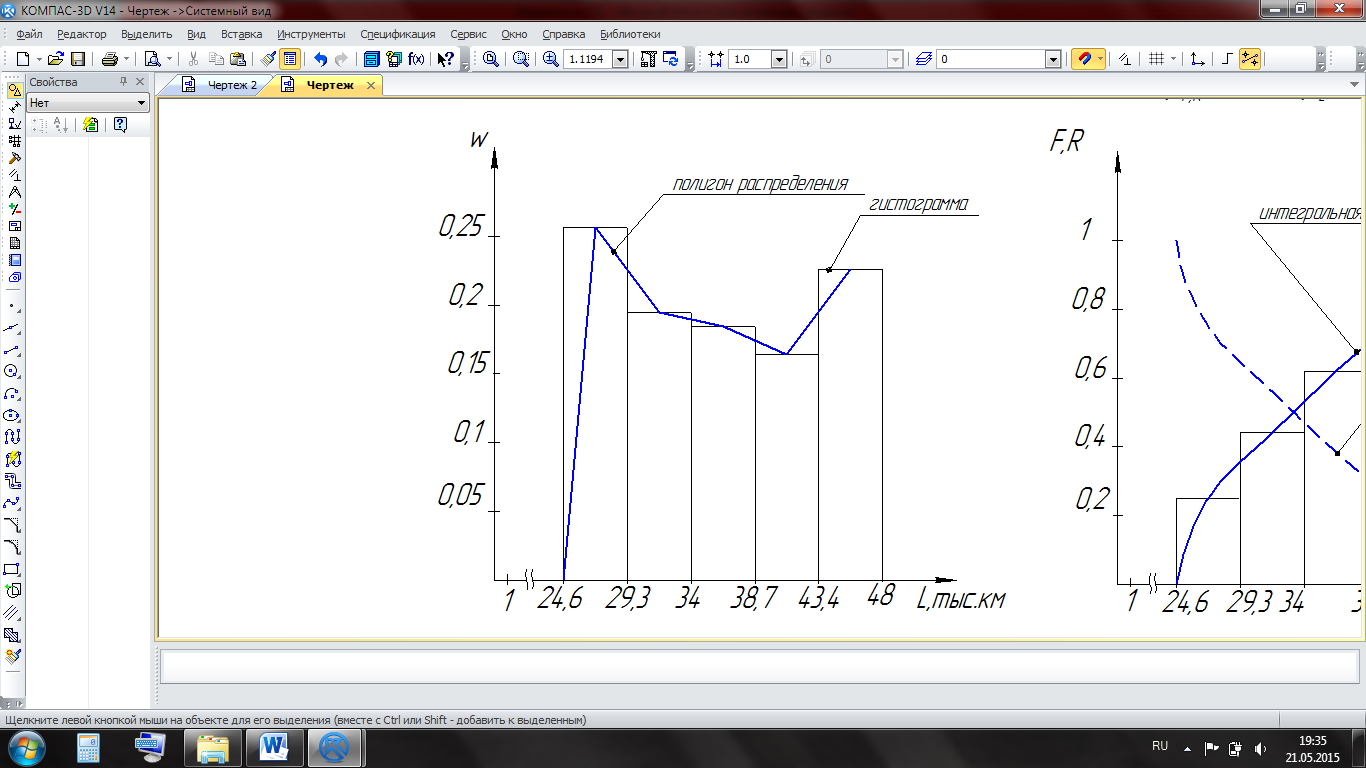
Рисунок 5.5 – Графическое изображение случайной величины
Наглядное представление о случайных величинах дает их графическое изображение интегральных функции распределения вероятностей отказа и безотказной работы (рисунок 5.6).
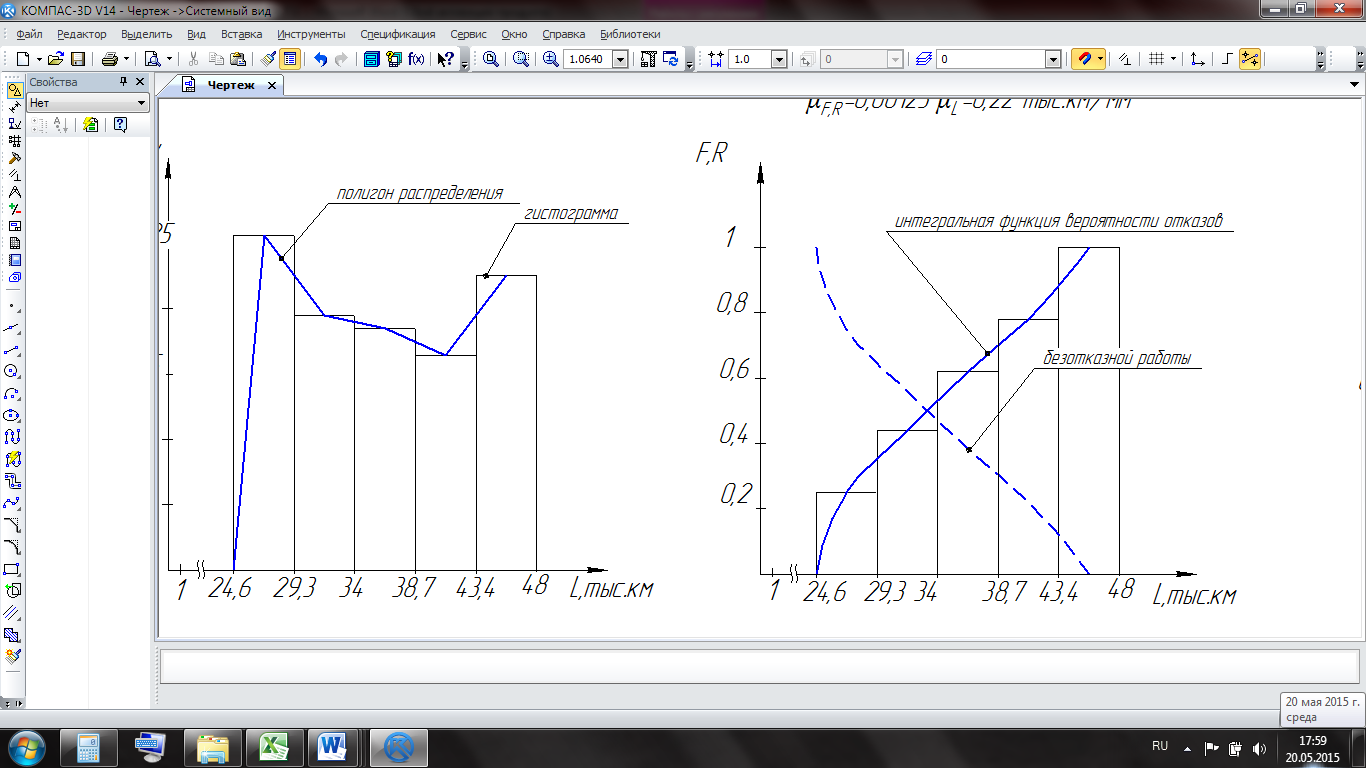
Рисунок 5.6 – Графическое изображение случайной величины
Наглядное представление о вариации случайной величины дает графическое изображение дифференциальной функции или закона распределения случайной величины (рисунок 5.7).
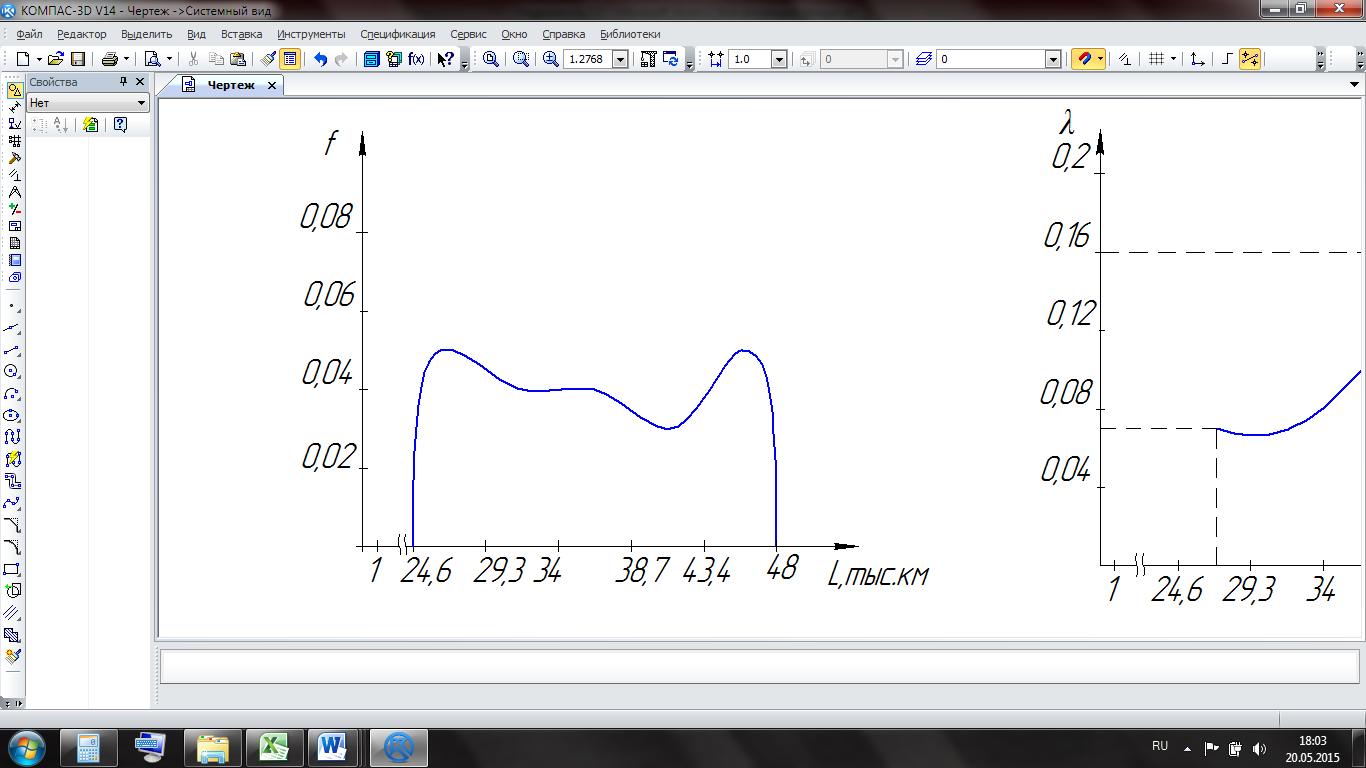
Рисунок 5.7 – Дифференциальная функция распределения
Наглядное представление о величине изменения интенсивности отказов l(L) реализуется в виде графика (рисунок 5.8).

Рисунок 5.8 – Изменение интенсивности отказов
Ранее в курсовой работе были рассмотрены закономерности изменения параметров технического состояния автомобилей по наработке (времени или пробегу) и вариация параметров технического состояния. Эти закономерности достаточно точно характеризуют надежность автомобилей и их элементов, т.е. позволяют оценить среднюю наработку на отказ, вероятность отказа автомобиля при определенной наработке, ресурс агрегатов и др.
Для рациональной организации производства необходимо знать, сколько автомобилей с отказами данного вида будет поступать в зону ремонта в течение часа, смены, недели, месяца. Будет ли их количество постоянным или переменным и от каких факторов оно зависит, т.е. необходимо иметь информацию о надежности не только конкретного автомобиля, но и группы автомобилей, например автомобилей данной модели, колонны, АТП. При отсутствии этих сведений нельзя рационально организовать производство, т.е. определить необходимое число рабочих, размеры производственных площадей, технологическое оборудование, расход запасных частей и материалов. Взаимосвязи между показателями надежности автомобилей и суммарным потоком отказов для автомобиля и группы автомобилей изучают с помощью закономерностей ТЭА, которые характеризуют процесс восстановления – возникновения и (или) устранения потока отказов и неисправностей изделий по наработке.
Date: 2015-07-17; view: 1337; Нарушение авторских прав