Описание экспериментальной установки

Лабораторная работа №2

ИССЛЕДОВАНИЕ затухающих крутильных колебаний

Цель работы

Определение параметров колебательной системы – кру-тильного маятника с затуханием, колебания которого слу-жат моделью движения во многих задачах классической и квантовой физики.

Описание экспериментальной установки

Крутильный маятник (рис.2.1) представляет собой диск, закрепленный на упругой проволоке, другой конец которой зажат в неподвижном кронштейне. Для получения значений углов j поворота маятника служит градуированная шкала на диске.

Для проведения измерений диаметра проволоки, диамет-ра дисков, длины подвеса служат штангенциркуль и масштаб-ная линейка (указанные параметры установки могут быть заданы).

При повороте тела, закрепленного на упругом подвесе, на малый угол j происходит закручивание проволоки. При этом возникает возвращающий момент упругих сил, равный

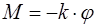, (2.1)

где 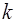– коэффициент кручения, зависящий от упругих свойств подвеса.

Используя уравнения динамики вращательного движения для крутильных колебаний, получаем

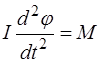(2.2)

или

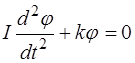, (2.3)

где 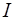– момент инерции диска.

Учитывая, что круговая частота гармонических колеба-ний определяется как

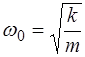, (2.4)

то из уравнения (2.3) и (2.4) имеем, что частота и период колебаний крутильного маятника равны соответственно

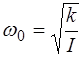, (2.5)

. (2.6)

В реальных колебательных системах (осцилляторах) про-исходит диссоциация (рассеяние) запасенной энергии, и сво-бодные колебания со временем затухают. Для учета процес-са рассеяния энергии в дифференциальное уравнение движения (2.3) необходимо ввести слагаемое, характеризу-ющее силу сопротивления движению:

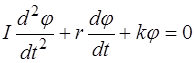, (2.7)

где – обобщенный коэффициент сопротивления, который для крутильного маятника является коэффициентом про-порциональности между тормозящим моментом (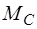) и уг-ловой скоростью :

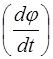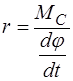. (2.8)

Решение уравнения (2.7) имеет вид:

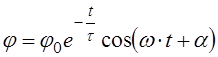(2.9)

где 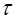– постоянная времени затухания, показывающая, что амплитуда колебаний

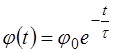
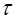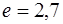уменьшается за время в раз.

Для крутильного маятника

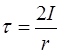. (2.10)

Частота затухающих колебаний

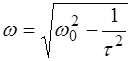(2.11)

меньше собственной частоты .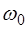

С увеличением момента трения постоянная времени 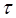уменьшается, и при 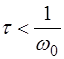частота 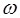(2.11) становится мнимой, колебания крутильного маятника прекращаются – движение становится апериодическим. Переход колебатель-ного движения в апериодическое происходит при условии, когда

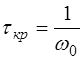. (2.12)

Энергия колебательного движения изменяется по закону

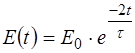, (2.13)

т.е. энергия осциллятора расходуется на работу против диссипативных сил и превращается во внутреннюю энергию.

Мощность потерь, т.е. скорость рассеяния энергии, с од-ной стороны,

,

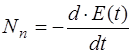а с другой, с учетом (2.13),

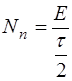. (2.14)

Качество колебательной системы, ее способность сохра-нять запасенную энергию характеризуется добротностью Q, которая определяется отношением запасенной энергии к потерям за время

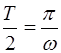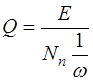; . (2.15)

Тогда с учетом (2.14) выражение (2.15) принимает вид:

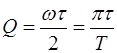. (2.16)

Из (2.16) следует, что добротность колебательной систе-мы равна числу колебаний за время 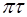; причем за это время амплитуда уменьшается в 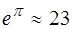раза, а энергия в 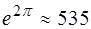раз.

Затухание колебаний принято характеризовать логариф-мическим декрементом затухания:

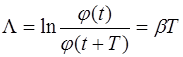, (2.17)

где – коэффициент затухания колебаний.

Следует отметить, что при малых декрементах затухания колебаний 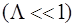, т.е. при большой добротности 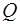осцил-лятора и с учетом (2.16), добротность равна:

. (2.18)

Date: 2015-06-11; view: 270; Нарушение авторских прав