Інтерполяція методом обернених середньозважених відстаней

Для даної теми «Інтерполяція спостережених полів (по нерегулярній мережі)» було обрано середовище програмування Pascal, яке використовується в оболочці Delphi. В ході роботи був обраний метод обернених середньозважених відстаней.

Використання цього методу в даній роботі полягає в тому, що на початку ми маємо набір нерівномірно розкиданих точок, з якими в процесі дослідження ми будемо працювати. Виходячи з того, що сітка нерівномірна, а нам треба отримати рівномірну, ми маємо знайти мінімальне і максимальне значення масиву для того, щоб визначити крок, з яким ми будемо розбивати рівномірну сітку:

Xmax:= PGeoPoint(FSrcData[0])^.X;

Xmin:= PGeoPoint(FSrcData[0])^.X;

Ymax:= PGeoPoint(FSrcData[0])^.Y;

Ymin:= PGeoPoint(FSrcData[0])^.Y;

Hmax:= PGeoPoint(FSrcData[0])^.H;

Hmin:= PGeoPoint(FSrcData[0])^.H;

for i:= 1 to FSrcData.Count - 1 do begin

if Xmax < PGeoPoint(FSrcData[i])^.X then Xmax:= PGeoPoint(FSrcData[i])^.X; if Xmin > PGeoPoint(FSrcData[i])^.X then Xmin:= PGeoPoint(FSrcData[i])^.X;

if Ymax < PGeoPoint(FSrcData[i])^.Y then Ymax:= PGeoPoint(FSrcData[i])^.Y if Ymin > PGeoPoint(FSrcData[i])^.Y then Ymin:= PGeoPoint(FSrcData[i])^.Y; if Hmax < PGeoPoint(FSrcData[i])^.H then Hmax:= PGeoPoint(FSrcData[i])^.H;

if Hmin > PGeoPoint(FSrcData[i])^.H then Hmin:= PGeoPoint(FSrcData[i])^.H; StatusBar.Panels[0].Text:= 'Знаходимо мін. і макс. точки ' + IntToStr(i);

Application.ProcessMessages;

end;

Вивід максимальних і мінімальних даних:

a1:= floattostr (Xmax);

a2:= floattostr (Xmin);

a3:= floattostr (Ymax);

a4:= floattostr (Ymin);

Label6.Caption:=a1;

Label7.Caption:=a2;

Label8.Caption:=a3;

Label9.Caption:=a4;

Знайшовши мінімальне і максимальне значення, ми повинні розбити наш масив на рівномірну сітку з певним кроком, використовуючи наступні формулу:

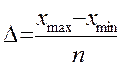
Xdelta:= Xmax - Xmin;

Ydelta:= Ymax - Ymin;

Hdelta:= Hmax - Hmin;

Xcount:= Round(Int(Xdelta / CellWidth));

Ycount:= Round(Int(Ydelta / CellWidth));

StatusBar.Panels[0].Text:= 'Розрахунок закінчений '

Наступний блок програми стосується безпосередньо реалізації обраного методу.Використовуємо основну формулу методу обернених середньозважених відстаней:

;

Маємо:

SetLength(ResData, Xcount);

for i:= 0 to XCount - 1 do SetLength(ResData[i], Ycount);

for i:= 0 to Xcount - 1 do for j:= 0 to YCount - 1 do begin

StatusBar.Panels[0].Text:= 'Розраховуємо вузли регулярної сітки (розмір ' + IntToStr(Xcount) + 'x' + IntToStr(Ycount) + '): X=' + IntToStr(i) + ', Y=' + IntToStr(j);

Application.ProcessMessages;

Summ1:= 0;

Summ2:= 0;

for z:= 0 to FSrcData.Count - 1 do begin

d:= sqr((i * CellWidth + Xmin) - PGeoPoint(FSrcData[z])^.X) +

sqr((j * CellWidth + Ymin) - PGeoPoint(FSrcData[z])^.Y);

h:= sqrt(d + sqr(Delta));

Summ1:= Summ1 + PGeoPoint(FSrcData[z])^.H / Power(h, Beta);

Summ2:= Summ2 + 1 / Power(h, Beta);

end;

ResData[i][j]:= Summ1 / Summ2;

hh:= Summ1 / Summ2;

stringGrid1.Cells[3,k+1]:=floattostr(hh);

StringGrid1.RowCount:=k+2;

k:=k+1;

writeln(fout,xx:3:4,' ', yy:5:5,' ', hh:5:5);

end;

closeFile(fout);

Для контролю розрахованих вузлів інтерполяції виводимо їх та розраховані по них значення у таблицю:

stringGrid1.Cells[0,0]:='№'; //введення шапки таблиці

stringGrid1.Cells[1,0]:='x=';

stringGrid1.Cells[2,0]:='y=';

stringGrid1.Cells[3,0]:='h=';

stringGrid1.Cells[0,k+1]:+=intTostr(k+1); //заповнення табл. даними про точки

stringGrid1.Cells[1,k+1]:=floattostr(xx);

stringGrid1.Cells[2,k+1]:=floattostr(yy);

stringGrid1.Cells[3,k+1]:=floattostr(hh);

stringGrid1.RowCount:=k+2;

Після цього вже відбувається виведення на екран регулярної сітки:

rHmax:= Round(ResData[0][0]);

rHmin:= Round(ResData[0][0]);

for i:= 0 to Xcount - 1 do for j:= 0 to YCount - 1 do begin

if rHmax < Round(ResData[i][j]) then rHmax:= Round(ResData[i][j]);

if rHmin > Round(ResData[i][j]) then rHmin:= Round(ResData[i][j]);

end;

rHdelta:= rHmax - rHmin;

Image.Picture.Bitmap.Width:= Xcount;

Image.Picture.Bitmap.Height:= Ycount;

for i:= 0 to Xcount - 1 do for j:= 0 to YCount - 1 do

begin

c:= Round(Int((ResData[i][j] - rHmin) * 256 / rHdelta));

Image.Picture.Bitmap.Canvas.Pixels[Xcount - i + 1, j]:= RGB(c, c, c);

StatusBar.Panels[0].Text:= 'Виводим на екран регулярну сітку';

Application.ProcessMessages;

end;

Схожим чином виводимо на екран вихідні точки:

for i:= 0 to FSrcData.Count - 1 do

begin

Image.Picture.Bitmap.Canvas.Pixels[Xcount + 1 - Round(Int((PGeoPoint(FSrcData[i])^.X - Xmin) / CellWidth)),

Round(Int((PGeoPoint(FSrcData[i])^.Y - Ymin) / CellWidth))]:= RGB(0, 0, 255);

StatusBar.Panels[0].Text:= 'Виводимо на екран вихідні точки...';

Application.ProcessMessages;

end;

end;

Для перевірки використаного та запрограмованого алгоритму були обрані дані, які отримали в результаті дослідження на Рівненській атомній електорстанції, а саме стан ґрунтів, рівень ґрунтових вод (РГВ), процесів карстоутворення та суфозії. Дані представляють собою усередненні значення за рівнем грунтових вод(96 точок).

В результаті ми провели серію дослідів, де отримали проінтерпольовану карту (як приклад взяли біля 50000 нових точок).

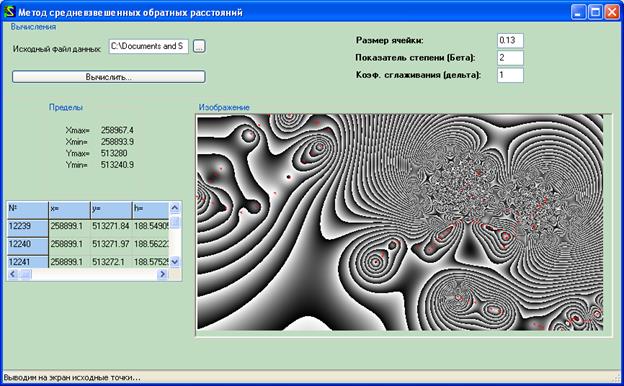
Рис.2 Проінтерпольвана карта з даними

ВИСНОВКИ

Під час написання курсової роботи було розроблено і реалізовано алгоритм і проведено інтерполяцію за даними Рівненської атомної електростанції, а саме рівнем грунтових вод, процесу карстоутворення і суфозії.

В ході нашої роботи обраний один з найбільш широко використовуваних методів інтерполяції – метод обернених середньозважених відстаней (Inverse Distance Weighting). В цьому методі вплив кожної конкретної точки визначається відстанню до вузла сітки, тобто її вагою.

В роботі автор наочно переконалась в недоліках методу обернених середньозважених відстаней. Серед них: низька швидкість роботи на великих обсягах даних: обчислення інтерполянта має трудомісткість; алгоритм надає занадто багато ваги віддаленим вузлам, їх сумарна вага може виявитися більше, ніж вага вузлів, розташованих поряд з точкою інтерполяції тощо.

Автор вбачає, що основні недоліки цього методу можуть бути усунені, якщо застосувати модифікацію Шеперда.

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ:

1. Дэвис Дж. Статистический анализ данных в геологии В 2 кн., Кн.1. / Дж. Дэвис. – М.: Недра, 1990. – 319 с.

2. Никитин А. А. Теоретические основы обработки геофизической информации: учебник для вузов / А. А. Никитин. – М., 1986. – 342 с.

3. Лященко М. Я., Головань М. С. Чисельні методи: Підручник.- К.: Либідь, 1996.-288 с.

4.http://www.emsi.com/smshelp/Data_Module/Interpolation/Inverse_Distance_Weighted.htm

Date: 2016-07-25; view: 259; Нарушение авторских прав