Метод обернених середньозважених відстаней

В ході дослідження даної тематики було обрано метод обернених середньозважених відстаней (inverse distance weighting), оскільки він простий в реалізації. Як було сказано вище, метод оберненоих середньозваженоих відстаней - це спосіб багатовимірної інтерполяції на нерегулярній сітці, процес присвоєння значення невідомої точки, використовуючи значення зазвичай розкиданих відомих точок. Це один з найбільш широко використовуваних методів для інтерполяції. У цьому методі вплив кожної конкретної точки визначається відстанню до вузла сітки, тобто її вагою.

Розглянемо найпростіший варіант IDW-алгоритма:

; ,

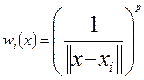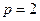
Нехай x_i - це набір точок у просторі, а y_i - значення функції в цих точках.

w_i - ваговий коефіціент;

x- x_i – відстань між точкою, яку треба знайти і даною точкою;

p – степінь відстані.

Спосіб інтерполяції, заснований на використанні величин, зворотних відстаням між вузлами інтерполяції, зведеним у деяку ступінь, універсальний, легко реалізується і зрозумілий, а також володіє високим ступенем точності.

Рис.1Приклад розташування точок при методі IDW
Рисунок 1 показує, що у кожному з цих вузлів оцінена властивість зважується з урахуванням зворотних відстаней від оцінюваної(початкової). Зважені властивості потім сумуються і діляться на суму вагів.

Ватсон (Watson) і Філіп (Philip) в 1985 році склали список деяких обмежень використання цього методу, наприклад, його не можна використовувати для випадку радіальної симетрії, коли в результаті такої інтерполяції можуть з'явитися елементи невиправданої лінійності.

Експериментально було показано, що для p=1 повна похідна функції z = f(x, y) у вузлах інтерполяції зазнає розрив. Зазвичай значення p підбирається емпірично для конкретного завдання. Значення 1,65 і 2 вибиралися для p Келвеєм (Kelway, 1974) для прогнозування кількості опадів, що випадають. У той час, як модель ARMOS (1990) для виявлення родовищ нафти рекомендує використовувати значення р від 4 до 8.

У такому формулюванні алгоритм носить як переваги, так і недоліки.

Переваги методу:

1)Гранична простота реалізації.

2) Відсутність параметрів, що потребують в налаштуванні.

3) Працездатність в просторі будь-якої розмірності.

4) Працездатність на будь-який рівномірної / нерівномірною сіткою.

5)Алгоритм "не помічає" мультиколінеарності даних, здатний успішно працювати, навіть якщо всі крапки сітки вкладені в підпростір меншої розмірності. При правильній реалізації алгоритм успішно працює навіть на сітках із співпадаючими вузлами.

Недоліки алгоритму:

1) Низька швидкість роботи на великих обсягах даних: обчислення інтерполянта має трудомісткість.

2) Алгоритм надає занадто багато ваги віддаленим вузлам. Їх сумарна вага може виявитися більше, ніж вага вузлів, розташованих поряд з точкою інтерполяції. Це особливо виражено в просторах високої розмірності.

3) Глобальність інтерполяції сама по собі є проблемою, тому що інтерполянт стає більш чутливий навіть до далеких викидів. У вузлах інтерполяції функція f(x) плоска, тобто має нульову похідну.

Існує також модифікований метод Шепарда, який майже не має значних відмінностей від методу оберненої середньозваженої відстані. Метод Шепарда теж використовується для інтерполяції на нерівномірній сітці. Можна сказати, що це та ж сама середньозважена інтерполяція, тільки зважуються в ній не значення в точках, а опорні функції. На відміну від методу оберненої середньозваженої відстані метод Шепарда використовує квадрати відстані.

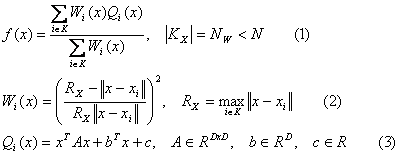
Де:

K- підмножина точок;

N_w – кількість точок в області;

W_i (x)- вагова функція;

Q_i (x)- вузлова функція;

Метод Шепарда відрізняється від оригінального алгоритму тим, що:
1) Для інтерполяції використовується підмножина точок K потужністю N_w – множина N_w найближчих сусідів точки x.

2) Вагові функції W_i (x) мають більш складний вигляд. Тепер вони перетворюються в нуль на кордоні сфери, радіус якої дорівнює радіусу множині N_w найближчих сусідів точки x.

3) Замість константних значень y_i під зваженням суми тепер беруть участь вузлові функції Q_i (x). Ці функції можуть бути квадратичним, лінійними або константним (за вибором користувача). Q_i (x) виходить в результаті зваженої апроксимації по МНК множини N_q найближчих сусідів точки x_i з обмеженням Q_i (x_i) = y_i. Вагові коефіцієнти завдання МНК вибираються за формулою (2).

Основними перевагами модифікованого алгоритму є:

1) Всього два потрібних для налаштування параметра: N_w і N_q. Оптимальні значення знаходяться перебором.

2) Працездатність в просторі будь-якої розмірності.

3) Працездатність на будь-який рівномірній / нерівномірній сітці. Алгоритм "не помічає" мультиколінеарності даних, здатний успішно працювати, навіть якщо всі точки сітки вкладені в підпростір меншої розмірності. Алгоритм успішно працює навіть на сітках із співпадаючими вузлами.

4) Відсутність "плоских плям" в околицях вузлів (при використанні квадратичних або лінійних вузлових функцій).

5) Локальність інтерполяційний схеми. Значення f (x) залежить тільки від найближчих до точки x вузлів, що вирішує ряд проблем і істотно покращує якість інтерполяційний схеми.

6) Можливість використовувати алгоритм для вирішення завдань регресії, тобто для роботи з зашумленими даними.

Можна відзначити наступні недоліки алгоритму:
1) Алгоритм перевершує за швидкістю оригінальний IDW-алгоритм тільки на великих наборах точок (порядку декількох сотень).
2) Хоча алгоритм працездатний на будь-який сітці, швидкодію знижується, якщо точки вкладені в підпростір меншої розмірності.
3) У деяких рідкісних випадках f (x) може мати розриви. Розрив виникає, якщо більш ніж N_w найближчих сусідів точки x знаходяться на абсолютно однаковій відстані від неї.

Date: 2016-07-25; view: 387; Нарушение авторских прав