Основные свойства пределов последовательностей.

Предел числовой последовательности.

Введение.

Начало изучению понятия предела положено в средней школе. Там с помощью предельных переходов определяется длина окружности, площади боковых поверхностей и объёмы цилиндра и конуса, площади поверхности и объём шара. Понятие предела использовано также при определении суммы бесконечно убывающей геометрической прогрессии. Нам предстоит изучить теорию предела на более общей основе, с необходимой глубиной и строгостью, что позволит расширить круг приложений теории пределов к решению теоретических и практических задач.

Понятие предела вместе с понятием функции составляют основу математического анализа. Все остальные разделы курса так или иначе используют теорию пределов.

I. Числовая последовательность и её предел.

Определение. Если каждому числу из натурального ряда чисел поставлено в соответствие вещественное число , то множество вещественных чисел (1) называется числовой последователь-ностью, или просто последовательностью.

Числа будем называть элементами (или членами) последовательности (1), - общим членом последовательности, а число - его номером. Сокращенно последовательность (1) будем обозначать символом 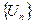. Так, например, символ 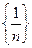обозначает последовательность . Формула, задающая , называется формулой общего члена последовательности 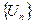. С помощью этой формулы можно вычислить любой элемент этой последовательности.

Например, дана формула общего члена последовательности . Написать пять первых её элементов. Положив последовательно в общем члене получим

Формула, задающая , не являются единственной. Так, например, последовательность –1,1..-1,1,… задается формулой , или . Не всегда последовательность 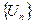можно задать аналитически.

Последовательность считается заданной, если указан способ получения любого её элемента. По своему определению, последовательность содержит бесконечное число элементов.

Геометрически последовательность 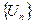изображается на числовой прямой в виде последовательности точек, координаты которых равны соответствующим элементам последовательности.

Например, .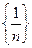

0 U₄ U₃ U₂ U₁

1

Определение. Последовательность 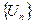называется ограниченной сверху (снизу), если существует число (число ) такое, что любой элемент этой последовательности удовлетворяет неравенству .

Последовательность 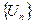называется ограниченной, если она ограничена и сверху и снизу.

Последовательность 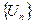называется неограниченной, если для любого положительного числа существует элемент этой последовательности, удовлетворяющий неравенству .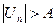

Например: 1) последовательность ограничена снизу ; 2) ограничена 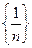ограничена , т.е. 3) последовательность неограниченная.

Определение. Число 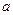называется пределом числовой последовательности 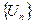, если для любого положительного числа существует номер такой, что при выполняется неравенство (2).

При этом последовательность 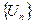называется сходящейся.

Если последовательность 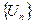сходится и имеет своим пределом число 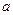, то символически это записывается так: .

Последовательность, не являющаяся сходящейся, называется расходящейся.

Замечание. Предел числовой последовательности имеет геометрическое истолкование. Неравенство (2) равносильно неравенствам , или , которые означают, что элемент находится в - окрестности точки .

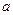Поэтому определение предела последовательности можно сформулировать следующим образом: число 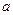называется пределом последовательности 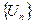, если для любой окрестности точки 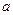существует номер такой, что все элементы с номерами находятся в этой окрестности.

Основные свойства пределов последовательностей.

Теорема 1. Сходящаяся последовательность имеет только один предел.

Теорема 2. Сходящаяся последовательность ограничена.

Теорема 3. Алгебраическая сумма, произведение двух сходящихся последовательностей есть сходящаяся последовательность, предел которой равен соответственно алгебраической сумме, произведению пределов последовательностей, т.е. .

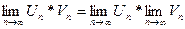Теорема4. частное двух сходящихся последовательносте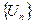й и при условии, что , есть сходящаяся последовательность, предел которой равен частному пределов последовательностей, т.е. .

Рассмотрим последовательность 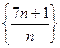. С одной стороны , с другой стороны .

Получено неверное равенство 7=1, так как допущена грубая ошибка: неправильно применена теорема о пределе частного, т.к. последовательности и не имеют конечных пределов.

Запись не обозначает никакого числа, а является лишь выражением того, что элементы последовательности 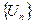по абсолютной величине неограниченно возрастает. Поэтому с символом нельзя обращаться как с числами и писать , или , или .

Последовательность называется бесконечно малой последовательностью (б.м.п.), если для любого существует номер такой, что для любого выполняется неравенство:

Последовательность называется бесконечно большой (б.б.п.), если для любого существует номер такой, что для любого выполняется неравенство:

Свойства бесконечно малых последовательностей

Свойство 1. Произведение бесконечно малой последовательности и ограниченной последовательности 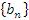есть бесконечно малая последовательность .

Свойство 2. Сумма любого конечного числа бесконечно малых величин есть величина бесконечно малая.

Date: 2016-07-25; view: 640; Нарушение авторских прав