Концентрация носителей заряда и положение уровня Ферми в полупроводниках

Число электронов в зоне проводимости с энергиями от E до E+dE будет определяться произведением плотности уровней в зоне проводимости на вероятность их заполнения, т.е.

, (9)

где N(E) – плотность квантовых состояний, а 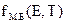- функция распределения Максвелла-Больцмана.

Тогда количество электронов в зоне проводимости будет равно

(10)

где E₁ и E₂ - границы зоны проводимости.

Обычно отсчет энергии электронов в полупроводнике проводят от уровня 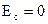. В качестве верхней границы зоны можно положить 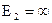, так как число электронов, находящихся в зоне, резко уменьшается с увеличением их энергии. Тогда из (10) можно получить

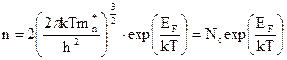, (11)

где 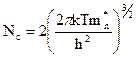(12)

есть эффективная плотность состояний в зоне проводимости.

В случае акцепторного полупроводника число дырок в валентной зоне определяется аналогично, но при этом вероятность образования дырки в зоне равна , где 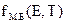- вероятность нахождения электрона на уровне E при температуре T. Интегрирование ведется в пределах от 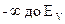. Тогда соответствующее выражение для дырок имеет вид

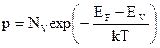, (13)

где (14)

есть эффективная плотность состояний в валентной зоне.

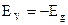Если отсчет энергии ведется от уровня , то , где 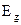- ширина запрещенной зоны полупроводника, и

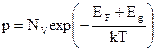(15)

Формулы (11) и (15) справедливы как для собственных, так и для примесных полупроводников. Однако значения E_f в этих случаях различны.

В собственном полупроводнике носители образуются при переходе электрона из валентной зоны в зону проводимости с образованием пары свободных носителей: электрона и дырки. Концентрации электронов в зоне проводимости и дырок в валентной зоне равны, т.е. 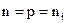- собственная концентрация носителей. Очевидно, что n_i, определяется величиной ширины запрещенной зоны 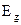данного полупроводника и его температурой Т.

Перемножив (11) и (15), получим:

(16)

Откуда для собственной концентрации получаем

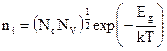(17)

Для заданных значений произведение

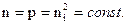
Соотношение

(18)

носит название закона действующих масс. В случае термодинамического равновесия этот закон справедлив и для примесных полупроводников, устанавливая связь между концентрациями основных и неосновных носителей в легированном полупроводнике:

(19)

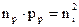(20)

Деля почленно (11) на (15), логарифмируя полученное выражение и учитывая, что 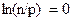при можно получить выражение для определения уровня Ферми:

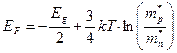(21)

Таким образом, при T=0 К уровень Ферми в собственном полупроводнике находится посередине запрещенной зоны, а с увеличением температуры он смещается к верху, если , или опускается к , если .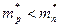

При увеличении температуры кристалла возрастает амплитуда тепловых колебаний атомов решетки, в результате чего усиливается перекрытие волновых функций их электронов. В свою очередь это вызывает увеличение ширины зоны проводимости и валентной зоны и соответственное уменьшение ширины запрещенной зоны. Изменение 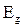с ростом T описывается соотношением

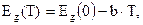(22)

где 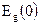- ширина запрещенной зоны при Т=0 К, b [эВ/К] - коэффициент изменения .

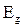Если известен уровень Ферми Е_F, то определить концентрацию носителей заряда можно, используя формулы (11) и (15). Однако положение уровня Ферми в этом случае требует определения.

Пусть имеется полупроводник n-типа с концентрацией допоров 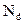. При низких температурах, когда энергия тепловых колебаний значительно меньше, чем энергия активации атомов примеси 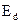, примесные электроны находятся на донорном уровне и зона проводимости полностью свободна. При увеличении температуры кристалла тепловая энергии 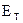, сообщаемая атомам примеси, возрастает и электроны начинают переходить с примесного уровня в зону проводимости, т.е. происходит ионизация атомов донороной примеси. В случае акцепторного полупроводника процесс ионизации примеси ведет к образованию носителей заряда в валентной зоне - дырок. В обоих случаях рост концентрации носителей заряда с изменением температуры происходит по экспоненциальному закону:

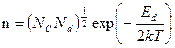(23)

(24)

При этом отсчет энергии примесного уровня ведется от края зоны. В логарифмическом масштабе концентрационные зависимост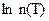и и в области низких температур представляют собой прямые (рис.2, участок 1).

Рис. 2. Зависимость концентрации носителей заряда в легированном полупроводнике от температуры:

1 – процесс ионизации примеси;

2 – примесь полностью ионизирована;

3 – переход к собственной концентрации

Положение уровня Ферми при этом для донорного и акцепторного полупроводников определяется соответственно выражениями

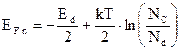(25)

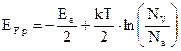(26)

При температуре 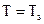, соответствующей условию 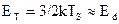, примесь практически будет ионизирована и дальнейшее увеличение температуры кристалла уже не будет влиять на концентрацию носителей - она будет оставаться постоянной и равной концентрации введенной примес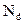и или 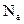(рис. 2, участок 2). В соответствии с (11)

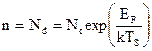(27)

Исходя из (27), при последующем увеличении температуры изменение Е_F (T) будет происходить линейно в соответствии с выражением

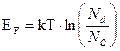(28)

При достаточно высоких температурах (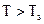) начнется ионизация атомов самого кристалла: под действием подрастающей тепловой энергии валентные электроны приобретают способность к преодолению запрещенной зоны с образованием пары: электрон в зоне проводимости и дырка в валентной зоне. Процесс увеличения концентрации собственных носителей заряда, как следует из (17), зависит от температуры тоже экспоненциально (рис. 2, участок 3). Когда концентрация собственных носителей заряда превысит концентрацию введенной в полупроводник примеси, т.е. при выполнении условия или , проводимость в кристалле станет собственной, а уровень Ферми coвпадет с Е_F собственного полупроводника.

Так как энергия активации примеси 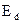(для акцепторов – 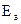) составляет около 0,01 эВ, а энергия тепловых колебаний атомов решетки Е_т при 300 К приблизительно равна 0,04 эВ, т.е. 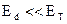, то в нормальных условиях вся примесь уже полностью ионизирована. Следовательно, концентрация носителей в примесном полупроводнике при Т=300 К определяется концентрацией введенной примес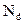и или .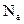

Если в полупроводнике одновременно присутствуют как донорная, так и акцепторная примеси, то полупроводник называется компенсированным. Электроны донорной примеси, стремясь занять состояния с минимальной энергией, будут переходить на акцепторные уровни, ионизируя акцепторы. Тип проводимости при этом будет определяться разностью концентраций доноров 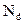и акцепторов 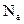. Если , то имеется образец n-типа, а если 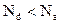, то p-типа. При равенстве концентраций доноров и акцепторов полупроводник называют полностью скомпенсированным. В этом случае проводимость в полупроводнике будет обусловлена собственными носителями заряда, однако из-за большого количества ионов примесей электропроводность такого полупроводника будет существенно ниже, чем собственного.

При нормальных условиях энергия, необходимая для образования носителей заряда, приобретается за счет тепловых колебаний атомов. Обмениваясь энергией при своем взаимодействии с решеткой в процессе движения, носители заряда находятся в тепловом равновесии с кристаллической решеткой. Поэтому их называют равновесными (стационарными) и обозначают .

Появление в полупроводнике свободных носителей заряда может быть связано также с действием внешней энергии. Под действием света, ионизирующих частиц, в процессе инжекции и т.д. в локальном объеме полупроводника возникают избыточные (по сравнению с равновесными) носители заряда , а полная концентрация носителей в нем становится равной 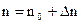. В момент генерации избыточные носители не находятся в тепловом равновесии с решеткой, и их называют неравновесными.

После прекращения воздействия концентрация неравновесных носителей вследствие процессов рекомбинации быстро убывает. Среднее время, которое проводит носитель заряда в свободном состоянии, называется временем жизни неравновесных носителей 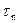. Так как каждый избыточный носитель живет в среднем 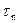секунд, то за одну секунду успеет прорекомбинировать электронов, где - избыточная концентрация в данный момент времени. Тогда скорость рекомбинации неравновесных электронов

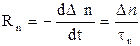(29)

Откуда для 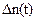получаем

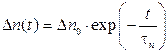(30)

где 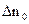– концентрация избыточных электронов в момент выключения внешнего воздействия (t=0).

Образование неравновесных носителей заряда в какой-либо области полупроводника ведет к установлению градиента концентрации носителей заряда (для одномерного случая dn/dx). B результате в полупроводнике наблюдается процесс диффузии носителей заряда, стремящийся выровнять разность концентраций. Диффузией называют процесс перемещения носителей заряда в направлении убывания их концентрации за счет собственного теплового хаотического движения. Плотность диффузионного тока 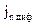определяется первым законом Фика:

(31)

если избыточные носители - электроны. Если же носители - дырки, то

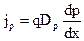(32)

где 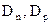- коэффициенты диффузии.

При одинаковом направлении градиента концентрации из-за различия в знаках заряда диффузионные токи текут в противоположных направлениях. Коэффициенты диффузии , также как и подвижности носителей заряда , определяются процессами рассеяния. Связь между соответствующими коэффициентами устанавливают соотношения Эйнштейна:

(33)

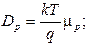(34)

Изменение концентрации неравновесных носителей вдоль полупроводника при удалении на расстояние х от места их генерации (x=0) описывается выражением

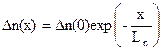(35)

где 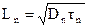- диффузионная длина электрона, т.е. среднее расстояние, которое проходит электрон за время своей жизни t_n до рекомбинации.

В случае дырок 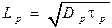, а выражение для выглядит аналогично (35).

Date: 2016-07-25; view: 1517; Нарушение авторских прав