Дифференциал функции, его геометрический смысл. Применение дифференциала в приближенных вычислениях

Функция f (х) называется дифференцируемой в точке х ₀, если ее приращение в этой точке можно представить в виде

(1)

где А ú, о(Δ х) – бесконечно малая функция более высокого порядка малости, чем Δ х при Δ х → 0.

ТЕОРЕМА. Для того, чтобы функция f (x) была дифференцируемой
в точке х ₀, необходимо и достаточно, чтобы в точке х ₀ существовала производная f ^' (x ₀) = А.

Следовательно, из (1) имеем

. (2)

Функция есть главная линейная часть приращения функции f (x) в точке х ₀. Эту главную линейную часть приращения функции f (x) и называют дифференциалом функции f (x) в точке х ₀ и обозначают

(3)

В частности, для f (x) = х имеем Следовательно, из (3):

. (4)

Выясним геометрический смысл дифференциала (см. рисунок):

ВД = ВС + СД; ВД = 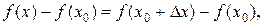ВС = Ð А =
= , так как АВ = , Ð А = .

Следовательно, из уравнения (2) имеем СД = о().

Таким образом, ВС =

Следовательно, с геометрической точки зрения, дифференциал функции равен приращению ординаты касательной, проведенной к графику функции в точке с абсциссой х ₀, при приращении аргумента .

Для дифференциалов функций f и g справедливы формулы, подобные формулам для производных функций:

1) ;

2) ;

3)

ПРИМЕР 3

Найти дифференциалы функций.

а) ;

б) ;

в) ;

г) ;

д)

.

Заметим, что dx = d (x + c), с ú, d (ax + в) = adx Þ dx = Данные формулы будут широко применяться при вычислении интегралов функций. С помощью дифференциала можно также приближенно вычислить значения функции f для х, близких к х ₀. Так, отбросив бесконечно малую функцию в формуле (2), получаем

. (5)

ПРИМЕР 4

Вычислить приближенно.

а) , б) .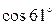

Решение

Воспользуемся формулой (5).

а)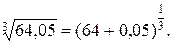

х ₀ = 64, = 0,05;

Следовательно:

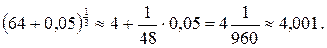
Заметим, что ;

б)

Þ

Заметим, что

ЗАДАЧИ И УПРАЖНЕНИЯ

Производная функции

Найти производные функций.

1.

2.

3. y = x cos x.

4.

5. Найти

6. у = sin 10 x.

7. у = sin³ 10 x.

8. у = sin⁴ x + cos⁴ x.

9.

10. у = 4 ^х + х ⁴.

11.

12. у = arcsin 2 x.

13. Найти , если

14.

15. у = (sin x) ^x.

Найти производную неявной функции.

16.

17.

18.

19.

20. Найти в точке М (1; 1), если

Найти производные третьего порядка от функций.

21.

22.

Составить уравнения касательной и нормали к следующим кривым
в указанных точках.

23. в точке (1; –3).

24. 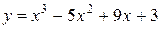в точке (2; 9).

25. Найти угол, под которым пересекаются линии: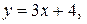

Date: 2016-07-25; view: 560; Нарушение авторских прав