Сложение двух параллельных сил. Пара сил

Как известно, две неравные и параллельные силы имеют равнодействующую.

Если силы направлены в одну сторону, то ,

.

Если силы направлены в разные стороны, то , , .

В случае, когда , и такая система сил не имеет равнодействующей .

Система двух равных по модулю параллельных сил, направленных в противоположные стороны – пара сил (неупрощаемая система сил).

h – плечо пары – расстояние между линиями действия сил.

Для характеристики действия пары сил на твердое тело вводится понятие момента пары.

Вектор момента пары сил равен векторному моменту одной из сил пары относительно точки приложения другой силы:

,

.

Он направлен перпендикулярно плоскости p действия пары в ту сторону, откуда видно, что вращение происходит против хода часовой стрелки.

Для пар, расположенных в одной плоскости, используется понятие алгебраического момента пары.

Алгебраический момент пары сил равен алгебраическому моменту одной из сил пары относительно точки приложения другой силы или, что то же самое, равен взятому со знаком плюс или минус произведению модуля одной из сил пары на плечо.

Момент пары положителен, если пара стремится повернуть плоскость против хода часовой стрелки.

Суммарное вращательное действие сил, составляющих пару, определяется следующей теоремой:

Теорема

Сумма моментов сил пары относительно произвольной точки равна моменту пары.

Доказательство:

Возьмем произвольную точку O. Сумма моментов сил пары относительно точки O:

,

так как , то

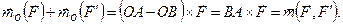
Теорема доказана.

Теоремы о парах

Основные свойства пар (правила их эквивалентного преобразования) даются следующими тремя теоремами:

Теорема 1

Две пары сил, лежащие в одной плоскости, эквивалентны, если равны их алгебраические моменты.

Следствие:

Пару сил можно перемещать в плоскости действия, изменяя величину плеча и силы, сохраняя ее момент.

Теорема 2

Пару сил можно переносить в любую плоскость, параллельную плоскости ее действия.

Следствие из теорем 1 и 2

Две пары сил эквивалентны, если равны их векторные моменты. (Вектор момента пары – свободный вектор).

Теорема 3

Две пары, лежащие в пересекающихся плоскостях, эквивалентны одной паре, момент которой равен геометрической сумме моментов составляющих пар.

В частном случае:

две пары, лежащие в одной плоскости, эквивалентны одной паре, момент которой равен алгебраической сумме моментов составляющих пар.

Из теоремы следует, что любую систему пар можно заменить одной парой, момент которой равен сумме моментов составляющих пар. Это позволяет получить условие равновесия системы пар.