Основные свойства электромагнитных волн.

С колебаниями и волнами мы сталкиваемся на каждом шагу как в повседневной жизни, так и при более глубоком изучении физики явлений.

Волна – это распространение колебаний в пространстве, происходящее с конечной скоростью. Волновой процесс – более сложная модель движения реальных систем (чем колебания – ограниченные, и чаще всего повторяющиеся, движения в окрестности некоторого среднего положения), состояние которых зависит уже не только от времени (колебания), но и от пространственных переменных. Поэтому такие процессы описываются уравнениями, содержащими частные производные.

Критериями перехода от колебательного движения к волновому может служить «условие квазистационарности»: если характерные размеры системы (где – скорость распространения возмущения, – время заметного изменения), процесс можно считать волновым, а систему – распределенной. Распространение электромагнитных волн происходит вследствие того, что появляющиеся в какой-либо точке пространства переменное электрическое поле возбуждает в соседних точках магнитное поле и наоборот.

Различие физических механизмов, реализующих волновой процесс, приводит к различным способам описания, основанным на сильно отличающихся друг от друга системах уравнений. Однако, для понимания наиболее фундаментальных явлений, свойственных волнам различной природы – интерференции, дифракции, дисперсии, отражения и преломления, рассеяния и т.д. – часто нет необходимости анализировать исходные сложные системы уравнений. Простые эффекты, как правило, описываются простыми, и поэтому универсальными математическими моделями.

Самым знаменательным моментом развития физики XIX столетия следует считать 1860 год, когда Дж.К.Максвелл сопоставил законы электричества и магнетизма с законами поведения света. Связав между собой открытые до тех пор законы, Максвелл обнаружил, что они несовместны, и, чтобы сделать всю систему совместной, он добавил член к уравнению , следовательно

.

Появление этого члена привело к предсказанию: часть электрического и магнитного поля спадает медленнее, чем обратный квадрат расстояния, а именно обратно пропорционально самому расстоянию .

.

Им было показано, что свет представляет собой электрическое и магнитное поля, распространяющиеся на большие расстояния, а генерируется свет быстрым колебанием электронов в атомах – все эти явления называются излучением, или, более точно, электромагнитным излучением. Движение атомов далекой звезды даже на огромных расстояниях возбуждает электроны нашего глаза, и мы узнаем о звездах. Если бы закона воздействия полей не существовало, мы бы буквально ничего не знали о внешнем мире.

Электрическое поле задается выражением

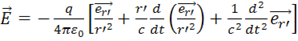. (1)

Рис.5. Напряженность поля , создаваемая положительным зарядом с запаздывающим .

Так как на поле в данный момент времени может влиять только поведение заряда в прошлом. Задержка во времени, или, так называемое, время запаздывания, есть время, необходимое для прохождения расстояния от заряда до точки измерения поля со скоростью света . Время запаздывания равно . В выражении (1) второй член учитывает запаздывание в первом грубом приближении. Это поправка к запаздывающему кулоновскому члену, она представляет собой произведение скорости изменения кулоновского поля и времени запаздывания. Третий член – вторая производная по единичного вектора, направленного к заряду.

Магнитное поле выражается следующим образом:

. (2)

Первый и второй члены уравнения (1) пропорциональны , а третий спадает обратно пропорционально первой степени расстояния

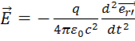. (3)

По мере движения заряда, единичный вектор крутится с ускорением 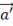по единичный сфере. Формула (3) дает полное и точное описание процесса измерения, в ней содержаться даже релятивистские эффекты.

Когда заряды движутся медленно, расстояния , которые они проходят с момента излучения, невелики, так что время запаздывания оказывается практически постоянным . В этом случае формула (3) упрощается.

Если заряженное тело сдвигается на малые расстояния и боковое смещение есть , то единичный вектор поворачивается на угол и поскольку практически постоянно, то составляющая 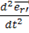в направлении равна просто ускорению самой величины в более ранний момент времени

. (4)

Сюда входит только составляющая , перпендикулярная лучу зрения, так как когда заряд движется к нам или от нас, единичный вектор в направлении заряда не смещается (рис.5) и ускорение равно нулю. Поэтому для нас существенно только боковое движение, то есть только та часть ускорения, которая проецируется на экран.

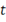Особый интерес представляет случай периодических колебаний заряда . Смещение зарядов в момент времени равнялось некоторой константе , амплитуда колебаний, умноженной на . Ускорение в этом случае равно

,где . (5)

Подставляя (5) в (4) получим

. (6)

(а)

(b)

Рис.6. (а) – ускорение некоторого заряда как функция ; (b) – электрическое поле как функция положения точки наблюдения спустя некоторый промежуток времени (множителем пренебрегаем).

Поле в каждой точке уравнения (6) определяется ускорением заряда в предыдущий момент, причем под словом «предыдущий» понимается секунд назад. Увеличив время на можно восстановить значение добавлением отрезка , то есть поле распространяется со временем как волна, уходящая от источника.

Итак, любая функция от аргумента выражает распространение возмущения вдоль оси в сторону возрастающих

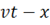или ; (7a)

Или в противоположную

или ; (7b)

В курсе теории электричества мы убедились, что следствием уравнений Максвелла является волновое уравнение. Это линейное уравнение в частных производных второго порядка гиперболического типа.

, (8)

где – оператор Лапласа, - константа, характеризующая свойства среды. Для электромагнитной волн это скорость распространения возмущения (волны), а – компоненты поля или .

Повторение.

Исходной системой уравнений для определения электромагнитного поля в среде являются уравнения Максвелла (все обозначения стандартны):

(9)

(10)

(11)

(12)

и закон сохранения полного электрического заряда внутри объема

(13)

Затем, взяв дивергенцию от обеих частей уравнений (10)

, (14)

так как ; перестановка операторов и правомерно в силу непрерывности векторного поля. Уравнение (11) можно получить взяв дивергенцию от уравнения (9).

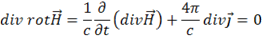
С учетом уравнения непрерывности (13)

.

Тогда

или .

Для расчета электромагнитных полей в различных средах систему уравнений (9) – (12) необходимо дополнить системой материальных уравнений:

, ,

В вакууме и , .

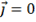Связь между и , и , и зависит от характера взаимодействия электромагнитного поля с веществом и может иметь очень сложный вид. Она может быть нелинейной, нелокальной, учитывать анизотропию и наследственные свойства («память») среды.

, , , (15’)

где , , – тензоры.

Предположим, что связь между векторами локальна и линейна. Материальные уравнения в этом случае имеют вид

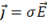, , , (15)

для изотропной среды , – электрическая и магнитная проницаемости среды (соответственно), – проводимость. Подставляя (15) в уравнение (11) и (13)

или ,

,

, или .

Откуда

,

Следовательно

,

Следовательно

в среде обладающей проводимостью, плотность свободных зарядов убывает со временем.

Простейшими решениями волновых уравнений, имеющими весьма большое значение, являются решения в виде плоских волн, В плоской волне возмущение s зависит только от расстояния, отсчитываемого вдоль некоторого фиксированного направления.

Система уравнений (9) – (13) с учетом уравнения (15) примет вид:

(16)

Исключив из системы (16) поле , получаем

.

Так как

Тогда

.

Следовательно

(17)

Если среда не обладает проводимостью, то есть , следовательно

или

Следовательно

или

. (18)

Или для однородной изотропной среды

.

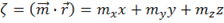
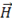и есть функция .

Для плоских волн оператор Лапласа

, .

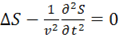Каждая из декартовых компонент векторов и будет при этом удовлетворять скалярному уравнению (18). Уравнение (18) описывает процесс распространения в направлениях со скоростью двух плоских волн.

и (19)

Аргумент - определяет фазу волны. Плоскость, на которой фаза волны постоянна, передвигается в пространстве со скоростью c. Возмущения, бегущие только в одну сторону (например, в положительном направлении (ось)), могут быть описаны также уравнением первого порядка

. (20)

Если вместо t ввести характеристическое время или «местное» время , то есть наблюдать за волной, двигаясь вместе с ней со скоростью ее распространения, то в новых переменных и уравнение (20) примет вид

. (21)

Решением этого уравнения является волна, не изменяющая формы своего профиля при изменении , то есть стационарная волна: .

Плоские волны, описываемые произвольными функциями 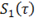и , часто удобно рассматривать как суперпозицию гармонических волн. Для этого необходимо, чтобы функции и 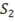можно было представить в виде интеграла Фурье

(22)

где

(23)

Подставляя (22) в (17) найдем, что функции будут решениями волнового уравнения, если их образы удовлетворяют уравнению Гельмгольца

. (24)

Решение (24) может быть записано в виде

, где (25)

Таким образом, функции под знаком интеграла (22) описывает гармонические плоские волны.

Переходя к декартовым координатам, фазу гармонической плоской волны можно записать в виде

,

где 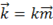. Уравнение определяет плоскость равной фазы. Если - действительный вектор, амплитуды волн постоянны всюду, в том числе и плоскости равной фазы. Строго говоря, функции будут удовлетворять уравнению Гельмгольца и в том случае, когда 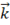- комплексный вектор

при условии

Тогда описывает плоскую неоднородную волну.

Для определения структуры этих волн необходимо обратиться к уравнению Максвелла. Рассмотрим волну, распространяющуюся в направлении . В этом случае

,

и система уравнений (9) – (12) будет иметь вид

(26)

Из последних двух уравнений (26), уравнений (с) и (d), следует, что

и

То есть проекции векторов и на направление распространения волны если и не равны нулю, то могут зависеть только от времени.

Умножая теперь скалярно первые два уравнения (26) на вектор получим

.

Иными словами, проекции и не зависят также от времени, то есть тождественно равны нулю. Это означает, что электромагнитные волны в диэлектрической среде являются поперечными волнами; векторы и лежат в плоскости фронта волны.

В проводящей среде , однако из уравнения , в случае 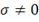следует, что или .

Продольная компонента вектора убывает во времени, а поэтому и в проводящей среде поле также поперечно.

Найдем теперь связь между векторами и в бегущей плоской волне. Вводя координату (характеристическое время) , связанную с волной, получим

, .

Первое из уравнений (26а) примет вид

Следовательно

(27)

Константу, получаемую при интегрировании по следует положить равной нулю, поскольку рассматриваются только переменные магнитного поля. Как следует из уравнения (27), векторы , и образуют правую ортогональную тройку векторов.

Величина

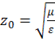(28)

определяющая количественную связь между напряженностями электрического и магнитного полей, называется импедансом среды.

– формула Максвелла. (29)

Величина называется показателем преломлением среды. Если направление векторов и в распространяющейся волне остается неизменным, волна называется линейно поляризованной. Часто возникает такое колебание, при котором в каждой фиксированной точке конец вектора (соответственно и ) движется по эллипсу – так называемая эллиптическая поляризация, частный случай – круговая поляризация. Но возможен другой предельный случай – эллипс может выродится в прямую.

,

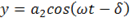
исключая время t получим

, .

Если , то

, если получаем круг.

Итак, волну, распространяющуюся со скоростью вдоль можно описать соотношением

(30)

или когда – есть синусоидальная (косинусоидальная) функция

, (31)

где 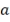– амплитуда, 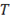– период, – фаза.

Значение зависит от и от , чтобы учесть это обстоятельство

(32)

– начальная фаза.

Функция (30) периодична по аргументу . Если дать приращение , то значение функции не изменится.

(33)

Введем обозначения:

– круговая частота, – волновое число.

Тогда

(34)

или вместо круговой частоты ввести число колебаний в секунду (частота)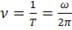

. (35)

Если вместо тригонометрических функций можно ввести экспоненциальные, уравнение (35) будет иметь вид

(36)

Волну, выраженную в одной из формул (31) – (36) будем называть монохроматической (, , ). Скорость распространения фазы определяется

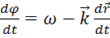=0 или .

Если фазовая скорость распространения монохроматической световой волны зависит от ее длины, то есть

,

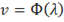то такие среды называются диспергирующими.

Ни одна реальная волна не длится бесконечно долго, а начинается и кончается в определенный момент времени. Такая волна не является строго монохроматической, так как ее амплитуда есть функция времени.

Рассмотрим пример: пусть волна описывается соотношением

, (37)

то есть 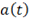раз в течение секунды достигает значение и столько же раз обращается в ноль, .

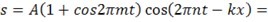
Следовательно, наша волна есть совокупность трех строго монохроматических волн с амплитудами , и и с частотами , , соответственно. Совокупность этих трех монохроматических волн составляет заданную немонохроматическую волну, описываемую уравнением (37).

Изменение амплитуды во времени означает вариацию интенсивности 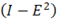и носит название модуляции. Модулировать можно не только амплитуду, но и фазу волны. Модуляция фазы тоже означает нарушение монохроматичности.

В нашем примере модуляция волны (воздействие на интенсивность) сопровождается расщеплением частоты монохроматической волны на , , (для оптических волн ).

Date: 2016-07-25; view: 358; Нарушение авторских прав