Метод максимального правдоподобия

Метод максимального правдоподобия точечной оценки неизвестных параметров заданного распределения сводится к отысканию максимума функции одного или нескольких оцениваемых параметров.

Дискретные случайные величины. Пусть 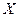- дискретная случайная величина, которая в результате 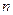опытов приняла возможные значения 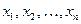. Допустим, что вид закона распределения величины 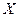задан, но неизвестен параметр 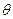, которым определяется этот закон. Требуется найти его точечную оценку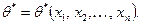

Обозначим вероятность того, что в результате испытания величина 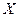примет значение через .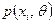

Функцией правдоподобия дискретной случайной величины 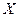называют функцию аргумента :

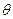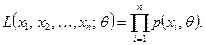
Оценкой максимального правдоподобия параметра 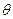называют такое его значение 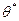, при котором функция правдоподобия достигает максимума.

Функци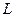и и 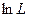достигают максимума при одном и том же значении 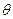, поэтому вместо отыскания максимума функции 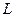ищут, что удобнее, максимум функции .

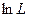Логарифмической функцией правдоподобия называют функцию .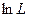

Точку максимума функции 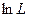аргумента 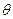можно искать, например, так:

1. Найти производную

2. Приравнять производную нулю и найти критическую точку 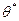- корень полученного уравнения (его называют уравнением правдоподобия).

3. Найти вторую производную если вторая производная при 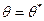отрицательна, то 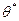- точка максимума.

Найденную точку максимума 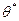принимают в качестве оценки максимального правдоподобия параметра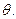

Непрерывные случайные величины. Пусть 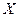- непрерывная случайная величина, которая в результате 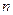испытаний приняла значения 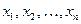. Допустим, что вид плотности распределения функции 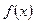задан, но неизвестен параметр 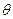, которым определяется эта функция.

Функцией правдоподобия непрерывной случайной величины 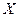называют функцию аргумента

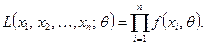
Оценку максимального правдоподобия неизвестного параметра распределения непрерывной случайной величины ищут так же, как в случае дискретной случайной величины.

Если плотность распределения 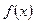непрерывной случайной величины определяется двумя неизвестными параметрам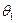и и 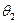, то функция правдоподобия есть функция двух независимых аргументов 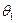и :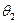

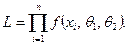
Далее находят логарифмическую функцию правдоподобия и для отыскания ее максимума составляют и решают систему

Примеры с решениями

Пример 1. Найти методом максимального правдоподобия точечную оценку неизвестного параметра 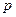(вероятность появления события в одном испытании) биномиального распределения:

где - число появлений события в 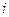-м опыте, 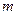- количество испытаний в одном опыте, 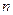-число опытов.

Решение. В данном случае функция правдоподобия имеет вид:

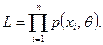
Учитывая, что 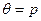и 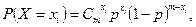получим

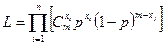
или

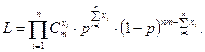
Напишем логарифмическую функцию правдоподобия:

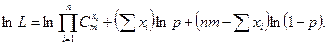
Найдем первую производную по :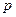

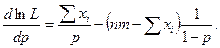
Приравняем первую производную нулю и решим полученное уравнение. Получим критическую точку:

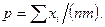
Найдем вторую производную по :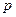

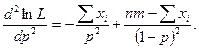
Легко проверить, что при вторая производная отрицательна, следовательно, эта точка есть точка максимума и ее надо принять в качестве оценки максимального правдоподобия неизвестной вероятности 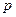биномиального распределения:

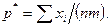
Очевидно, что если появлений события наблюдалось в 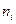опытах, то

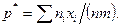
Пример 2. Найти методом максимального правдоподобия по выборке 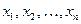точечную оценку неизвестного параметра 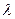показательного распределения, плотность которого

Решение. Составим функцию правдоподобия

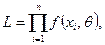
учитывая, что 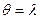и, следовательно,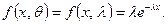

Найдем логарифмическую функцию правдоподобия:

Найдем первую производную по

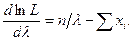
Запишем уравнение правдоподобия, для чего приравняем первую производную нулю:

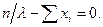
Найдем критическую точку, для чего решим полученное уравнение относительно

Найдем вторую производную по

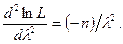
Легко проверить, что при 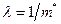вторая производная отрицательна, следовательно, эта точка есть точка максимума. Значит, в качестве оценки максимального правдоподобия надо принять величину, обратную выборочной средней:

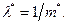
Задачи

Задача 1. Случайная величина 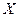имеет геометрическое распределение:

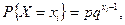
где - число испытаний, произведенных до появления события, 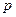- вероятность появления события в одном испытании, 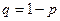. Найти методом максимального правдоподобия точечную оценку параметра .

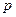Задача 2. Найти методом максимального правдоподобия по выборке 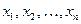точечную оценку параметра гамма-распределения (параметр 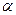известен), плотность которого

.

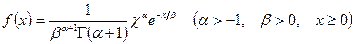Задача 3. Случайная величина 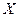(число появлений события 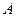в 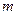независимых испытаниях) подчинена закону распределения Пуассона с неизвестным параметром :

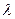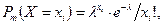
где 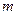- число испытаний в одном опыте, -число появлений события в 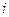-м опыте (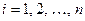). Найти методом максимального правдоподобия по выборке 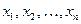точечную оценку неизвестного параметра 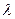распределения Пуассона.

Интервальные оценки

Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.

Доверительным называют интервал, который с заданной надежностью 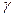покрывает заданный параметр.

Интервальной оценкой (с надежностью 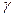) математического ожидания 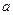нормально распределенной случайной величины 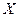по выборочной средней 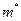при известном среднем квадратическом отклонении 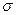служит доверительный интервал

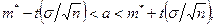
где 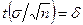- точность оценки, 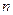- объем выборки, 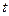- значение аргумента функции Лапласа , при котором .

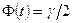При неизвестном 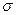(и объеме выборки )

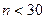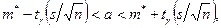
где 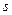- «исправленное» выборочное среднее квадратическое отклонение, 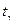находят по таблице распределения Стьюдента по заданным 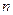и .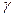

Примеры с решениями

Пример 1. По данным девяти независимых измерений некоторой физической величины найдены среднее арифметическое результатов измерений 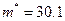и «исправленное» среднее квадратическое отклонение 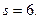Оценить истинное значение измеряемой величины с помощью доверительного интервала с надежностью 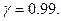Предполагается, что результаты измерений распределены нормально.

Решение. Истинное значение измеряемой величины равно ее математическому ожиданию 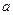. Поэтому задача сводится к оценке математического ожидания (при неизвестном 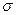) при помощи доверительного интервала

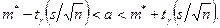
Все величины, кроме 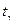, известны. Найдем 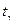с помощью таблицы распределения Стьюдента. При 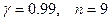находим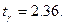

Подставив 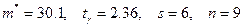в формулу для доверительного интервала, получаем искомый интервал:

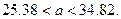
Пример 2. Найти доверительный интервал для оценки с надежностью 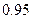неизвестного математического ожидания 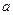нормально распределенной случайной величины 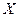генеральной совокупности, если генеральное среднее квадратическое отклонение 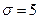, выборочная средняя 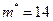и объем выборки .

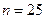Решение. Требуется найти доверительный интервал

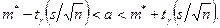
Все величины, кроме 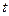, известны. Найдем 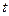из соотношения 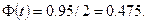По таблице значений функции Лапласа находим . Подставив в формулу для доверительного интервала, окончательно получаем

.

Пример 3. Найти минимальный объем выборки, при котором с надежностью 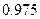точность оценки математического ожидания 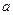генеральной совокупности по выборочной средней равна 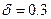, если известно среднее квадратическое отклонение нормально распределенной генеральной совокупности.

Решение. Воспользуемся формулой, определяющей точность оценки математического ожидания генеральной совокупности по выборочной средней: 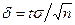. Отсюда

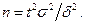
По условию, 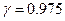, следовательно, 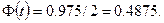По таблице значений функции Лапласа находим 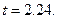Используя 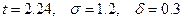, находим искомый объем выборки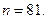

Задачи

Задача 1. Станок-автомат штампует валики. По выборке объема 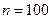вычислена выборочная средняя диаметров изготовленных валиков. Найти с надежностью 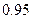точность 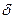, с которой выборочная средняя оценивает математическое ожидание диаметров изготовляемых валиков, зная, что их среднее квадратическое отклонение 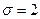мм. Предполагается, что диаметры валиков распределены нормально.

Задача 2. Одним и тем же прибором со средним квадратическим отклонением случайных ошибок измерений 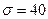м произведено пять равноточных измерений расстояния от орудия до цели. Найти доверительный интервал для оценки истинного расстояния 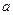до цели с надежностью , зная среднее арифметическое результатов измерений 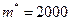м. Предполагается, что результаты измерений распределены нормально.

Задача 3. Из генеральной совокупности извлечена выборка объема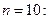

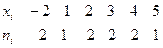
Оценить с надежностью 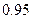математическое ожидание 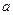нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала.

Date: 2016-07-25; view: 4167; Нарушение авторских прав