Графическое построение области допустимых решений

Задачи линейного программирования могут содержать тысячи переменных, однако на примере двух переменных можно наглядно показать структуру задачи, идею ее решения и возникающие проблемы.

Начнем с одного ограничения вида . Определим множество точек плоскости, удовлетворяющих этому условию. Сначала построим прямую линию и получим две полуплоскости. Для всех точек одной из них ограничение будет выполняться, а для другой нет, что и показано на рисунке. При его построении принято, что и , как это имеет место в реальных задачах, следовательно, можно ограничиться только первым квадрантом координатной плоскости.

Рис. 2.2

Для построения прямой проще всего найти точки ее пересечения с координатными осями, полагая поочередно одну из координат равной нулю. Чтобы определить, какая именно полуплоскость нужна, достаточно взять произвольную точку, не принадлежащую построенной прямой, и подставить ее координаты в неравенство. Если в качестве такой точки взять начало координат, то при ограничение будет выполняться. На рис. 2.2 это показано стрелкой, указывающей на выделяемую полуплоскость. Второй вариант выделения полуплоскости – около проведенной прямой с нужной стороны наносится короткая штриховка.

Для определения полуплоскости можно рассуждать и так: рассматриваемое ограничение при 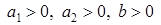– это ресурсное ограничение, которое не исключает неограниченный рост любой из переменных, но допускает их умеренные значения.

Ограничение вида при положительных коэффициентах не может выполняться при малых (в частности, нулевых) значениях обеих переменных одновременно, т. е. не ограничивает их рост. Ясно, что надо выделять полуплоскость, не содержащую начало координат.

Рассмотрим частный случай, когда , а знаки коэффициентов и разные, например, . Такая прямая (рис. 2.3) проходит через начало координат, но для ее построения нужна еще одна точка.

Проще всего взять точку . Чтобы правильно выделить полуплоскость достаточно заметить, что при и любом ограничение удовлетворяется.

Рис 2.3

Если последовательно нанести все заданные ограничения, то в зависимости от их сочетания получатся различные варианты области допустимых решений (рис. 2.4).

Выпуклый многоугольник Пустое множество

Выпуклая неограниченная Точка A

допустимая область

Луч Отрезок AB

Рис 2.4

Будем предполагать переменные неотрицательными, что не ограничивает общность, и перечислим все возможные случаи. Например, при трех ограничениях может получиться как треугольник, так и пустое множество. При увеличении числа ограничений, возрастет и число вершин, но многоугольник всегда будет выпуклым. Для случая пустого множества можно указать области, в которых выполняются любые два ограничения, но нет ни одной точки, удовлетворяющей всем трем ограничениям.

Когда одно из ограничений является равенством, что равносильно заданию двух неравенств с разными знаками, получаются луч и отрезок. Направленные в противоположные стороны стрелки показывают, что только точки прямой могут принадлежать области допустимых решений.

Во всех этих случаях получаются выпуклые фигуры. По определению, множество называется выпуклым, если каждая точка отрезка, соединяющего любые две его точки, также принадлежит этому множеству
(см. рис. 2.5).

Рис. 2.5

Ниже приведены примеры невыпуклых множеств (рис. 2.6).

Рис. 2.6

Date: 2016-07-25; view: 384; Нарушение авторских прав