
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Электр өрісінің кернеулік векторының ағыны. Гаусс теоремасы.
|
|
Электр өрісін сипаттайтын – электр өрісі кернеулігінің ағыны Φ деп аталатынжаңа физикалық шама енгізейік
 6.7 - сурет. ΔΦ элементар ағынның анықтамасына сәйкес
6.7 - сурет. ΔΦ элементар ағынның анықтамасына сәйкес
|  векторының ағыны өтетін өте кіші векторының ағыны өтетін өте кіші  элементар ауданды алайық. Оған түсірілген нормаль элементар ауданды алайық. Оған түсірілген нормаль 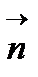 электр өрісінің векторы электр өрісінің векторы  -мен -мен  бұрышын жасайды делік. Бұл ауданды қиып өтетін элементар ағын бұрышын жасайды делік. Бұл ауданды қиып өтетін элементар ағын  : :
  · ·  ,
мұндағы ,
мұндағы  кернеулік векторының ауданға түсірілген кернеулік векторының ауданға түсірілген  нормаль бағытына проекциясы; нормаль бағытына проекциясы;  -вектор, ол модулі -вектор, ол модулі  -ке тең де, бағыты -ке тең де, бағыты  -нің бағытымен бағыттас. -нің бағытымен бағыттас.
|
Осыған байланысты атап өтетін бір жай: аудан тұйық болған кезде, оған түсірілген  нормальдың оң бағыты ретінде сыртқы нормаль алынады: яғни нормальдың бәрі ауданнан сыртқа қарай бағытталады.
нормальдың оң бағыты ретінде сыртқы нормаль алынады: яғни нормальдың бәрі ауданнан сыртқа қарай бағытталады.
Гаусс теоремасы:
 (6.13)
Бұл (6.13) теңдеу Гаусс теоремасының математикалық өрнегі болып табылады. Оның анықтамасы: вакуумдегі электр өрісі векторының кез келген пішіндегі тұйық бет бойынша ағыны, оның ішінде жатқан зарядтардың алгебралық қосындысын электр тұрақтысына (6.13)
Бұл (6.13) теңдеу Гаусс теоремасының математикалық өрнегі болып табылады. Оның анықтамасы: вакуумдегі электр өрісі векторының кез келген пішіндегі тұйық бет бойынша ағыны, оның ішінде жатқан зарядтардың алгебралық қосындысын электр тұрақтысына 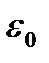 -ге бөлгенге тең. -ге бөлгенге тең.
|
Гаусс теоремасын қолдана отырып, келесі жағдайларда өрісті есептеуге болады:
1) Зарядталған радиусы R іші қуыс жіңішке, ұзын цилиндрдің электр өрісі:
 , (6.14)
, (6.14)
мұндағы r ≥ R, τ – зарядтардың сызықтық тығыздығы, яғни бірлік ұзындыққа келетін заряд шамасы.
Егер r < R, онда Е= 0. Бұл нәтиже зарядталған цилиндрдің R радиусына тәуелсіз, сондықтан оны біртекті зарядталған ұзын жіптің өрісін есептегенде де қолдануға болады.
2) Бірқалыпты зарядталған жазықтық өрісі:
 (6.15)
(6.15)
мұндағы σ – зарядтардың беттік тығыздығы, яғни бірлік ауданға келетін заряд шамасы.
Date: 2016-07-22; view: 2909; Нарушение авторских прав