Визначення множини шляхів заданої транзитності

Серед обмежень, які накладаються у процесі знаходженні шляхів у зв'язувальних мережах, можна розглядати обмеження на їх транзитність.

Під транзитністю шляху µ st розуміють кількість проміжних пунктів, які входять до нього (без урахування початкового s і кінцевого t пунктів), або кількість ліній зв'язку, які з'єднують на шляху тільки транзитні пункти. Кількість проміжних пунктів називають параметром транзитності Т на шляху µ st.

Обмеження за транзитністю на шляху надсилання повідомлення залежать від вимог до якості обслуговування у мережі (наприклад, до часу проходження повідомлення мережею, часу оброблювання повідомлення у вузлах та ін.).

Термінами теорії графів завдання формулюємо таким чином.

Дано деякий вихідний граф G(N, V), у відповідність множині N потужністю n вершин якого поставлено пункти зв'язувальної мережі, а множині V – лінії зв'язку. Необхідно визначити множину шляхів M ={µ si} із заданої вершини s до інших вершин i∈N, i ≠ s, i = 1,..., n, графа G, для яких параметр транзитності Т не перевищує певної заданої величини T0, тобто Т≤ T0, ∀ µ si, i ≠ s, i = 1...n.

Одним з найбільш зручних і легких для реалізування на ЕОМ методів визначення шляхів, які відповідають цій вимозі, є побудова так званого «ярусного дерева» шляхів від заданої вершини s до інших вершин графа.

На рисунку 6.12 наведено вихідний граф та відповідне йому «ярусне дерево» з параметром Т0 = 2.

Алгоритм побудови «ярусного дерева» складається з таких кроків.

Крок 0. Утворити підмножини нульового ярусу, який міститиме єдиний елемент – вершину s. Використовуючи матрицю суміжності, виписати номери стовпців у рядку з номером s, елементи якого дорівнюють asj = 1. Таким чином, отримано підмножину вершин першого ярусу, утворену вершиною s.

Крок 1. Утворити підмножину вершин наступного ярусу.

Для цього:

а) почергово вибирають вершини попереднього ярусу, для кожної з яких вибирають рядок з однойменною номером у матриці суміжності;

б) для кожного рядка виписують номери стовпців, визначені ненульовим елементами;

в) з кожної з утворених підмножин вилучають номери вершин (номери стовпчиків), відносно яких утворювалися підмножини вершин у попередніх ярусах. Усі невикреслені елементи (номери стовпчиків) утворюють підмножини наступного ярусу.

Крок 2. Якщо номер ярусу дорівнює (Т0 +1) – кінець.

Інакше – перейти до кроку 1.

Алгоритми знаходження екстремальних шляхів (найкоротших за довжині, за транзитністю) застосовують для визначення оптимальних маршрутів як у мережах із пакетною комутацією, так і в мережах із комутацією каналів. Результати їхньої роботи, зазвичай, зводять до побудови маршрутних матриць, які зберігаються в транзитних пунктах телекомунікаційних сегментів із комутованої топологією.

Вони призначені для визначення вихідного порту під час комутації вхід – вихід, наприклад, у маршрутизаторах, комутаційних телефонних станціях.

Спеціальні технічні можливості комутаційного обладнання іноді дають змогу вибирати додаткові напрями (обхідні) у разі зайнятості напрямку першого вибору. Порядок вибору напрямків визначають маршрутної матрицею, кількість рядків якої відповідає числу шляхів, нумерація рядків – призначеному порядку їх зайняття, а число стовпців – адресами пунктів призначення.

Елементом маршрутної матриці є номер порту вихідної лінії на шляху відповідного вибору з даного транзитного пункту до пункту призначення.

8. Задачі про потоки. Визначення потоку в зв’язувальної мережі. Умови збереження потоку в мережевому вузлі. Визначення перерізу мережі, теорема про величину максимального потоку. Методи й алгоритми знаходження максимального потоку в мережі.

У процесі будь-якого переміщення деяких об'єктів з одного пункту в інший виникають потоки і, якщо їх розглядати з урахуванням обмежень на переміщення, виникає потреба розв’язати задачу про знаходження максимальної величини потоку, який може існувати в умовах заданих обмежень.

Задачі про потоки в мережах (зважених графах) привертають особливу увагу завдяки специфіці своєї структури. Для подальшого роз’яснення необхідними є такі означення.

О з н а ч е н н я 1. Число хij називають потоком по дузі (ребру (і, j)), якщо хij≤ bij, де bij – пропускна здатність цієї дуги (ребра).

О з н а ч е н н я 2. Потоком Pst з деякої вершини s, яку називають джерелом, у деяку вершину t, яку називають стоком, у мережі є множина невід'ємних чисел хij - потоків по дугах (ребрах), якщо ці числа не суперечать таким обмеженням:

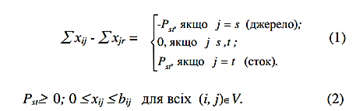
У даному випадку першу суму беруть по дугах, які ведуть до вершини j, а другу суму – по дугах із j.

Обмеження (1) вказує на те, що в кожну вершину (крім джерела та стоку) надходить стільки потоку, скільки з неї виходить, що називають умовою збереження потоку.

Обмеження (2) означає, що потік по дузі обмежено її пропускною здатністю.

Серед задач про потік найважливішою є задача про знаходження максимальної величини Pst у зваженому графі, де обмеженнями ваг дуг (ребер) є їх пропускні здатності.

Отже, задано деяка мережа G (зважений граф), у якій потрібно передати потік з однієї вершини в іншу. Може виявитися, що дуги (ребра) мережі G ненадійні. Якщо “достатню” кількість дуг (ребер) буде пошкоджено, мережа не зможе передати потрібний потік. Ця ситуація є аналогічною до вилучення певного числа дуг (ребер), у якій граф стає розділеним на декілька окремих компонент.

Якісне сприйняття подальшого матеріалу потребує визначень наступних термінів.

О з н а ч е н н я 3. Перерізом мережі називають мінімальне число дуг (ребер), вилучення яких з мережі порушує її зв'язність.

О з н а ч е н н я 4. Пропускною здатністю перерізу називають суму пропускних здатностей дуг, орієнтованих у напрямку від джерела до стоку, або ребер, які складають цей переріз.

О з н а ч е н н я 5. Переріз, який розділяє s та t та має найменшу пропускну здатність, називають мінімальним перерізом.

Мінімальний переріз, який розділяє джерело s та стік t, є аналогом «вузького місця» в мережі, а, отже, величина максимального потоку з s у t не може перевищувати його пропускну здатність. Таким чином, величина максимального потоку характеризує пропускну здатність мережі між двома цими точками.

Існує теорема, доведена Фордом і Фалкерсоном, яка затверджує, що велич ина максимального потоку завжди дорівнює мінімальній пропускній здатності перерізу, серед усіх які розділяють s та t. Теорема про максимальний потік і мінімальний переріз є основною в теорії потоків у мережах.

Отже, для оцінювання пропускної здатності зв'язної мережі достатнім є визначити величину максимального потоку з s у t, який вона може пропустити, причому обчислення його дугових компонентів, знаходження шляхів передавання може бути необов'язковим. Для цього, відповідно до теореми про максимальний потік і мінімальний переріз, достатнім є перебрати всі перерізи, які розділяють ці дві вершини, обчислити для кожного з них пропускну здатність і вибрати найменшу серед них.

Як бачимо, це завдання комбінаторної оптимізації.

Основна складність у ньому полягає в знаходженні ефективного методу породження множини перерізів, які розділяють s і t.

Класичними методами визначення множини перерізів у мережі є методи, які застосовують операції булевої алгебри над елементами матриць. Слід зауважити, що реалізація таких алгоритмів є досить трудомісткою для обчислювання.

Наведемо метод, який дає змогу уникнути зазначеного недоліку.

Нехай задано неорієнтований зважений граф G(N, V), де N – кількість вершин графа потужністю n, а V – кількість ребер, вагами яких є їх пропускні здатності bij (i,j = 1,2,... n).

Ребра, що складають переріз, котрий розділяє джерело s та стік t, будемо записувати за допомогою непересічних двох підмножин відповідно до початкових N1 та кінцевих N2 вершин, інцидентних цим ребрам.

Вершини підмножин N1 та N2 позначимо, наприклад, 0 – для вершин, що входять у N1, та 1 – для вершин, що входять в N2. Нехай джерело s належить N1, а стік t належить N2. Отже, вершина s буде позначена нулем, а t – одиницею.

Щоб знайти мінімальний переріз серед усіх можливих необхідно з’ясувати правило, яке порождає перерізи. Для цього запропоновано використовувати принцип подання чисел натурального ряду в двійковому вигляді. Розрядність двійкового числа в даному випадку визначається кількістю залишених непозначеними вершин і складатиме (n-2). Отже, максимальна кількість двійкових чисел дорівнює 2 (n-2). Ця ж величина відповідатиме максимально можливій кількості перерізів, які розділяють s та t.

Різні комбінації нулів та одиниць у кожному двійковому числі можна використовувати для розподілу (n-2) вершин на підмножини N1 і N2 для чергового перерізу.

Для зручності перенумеруємо всі вершини вихідного графа, використовуючи числа натурального ряду від 1 до n, як показано на рисунку 6.13. Далі організуємо лічильник від 0 до 2 (n-2), який буде генерувати двійкові числа розрядністю (n-2).

Кожній позиції двійкового числа необхідно поставити у відповідність номер непозначеної вершини (порядок не має значення). Нагадаємо, що вершини s та t тут не беруть участі, тому що вони від початку вже отримали позначки та відповідно розподілені в підмножини: s∈N1, t∈N2.

Після отримання чергового двійкового числа необхідно сформувати підмножини N1 і N2, зафіксувати перелік інцидентих їм ребер та визначити пропускну здатність відповідного перерізу.

Слід зазначити, що запропонований спосіб отримання переліку ребер, які складають деякий переріз, утворює ребра, які можуть бути відсутніми в фізичному графі. Ці ребра можна або вилучати з розгляду, або враховувати з нульовою пропускною здатністю.

Мінімальне серед усіх 2 (n-2) отриманих значень пропускних здатностей перерізів і буде відповіддю даної задачі – пропускною здатністю мережі з джерела s в стік t.

Формалізуємо зазначену процедуру покроковим алгоритмом.

Крок 0. Джерело (вершину s) позначити як «0», а стік (вершину t) – як «1». Покласти значення лічильника перерізів С рівним нулю. Сформувати сітку двійкового числа розрядністю (n-2), відповідно до кожній позиції якого поставити ідентифікатор (номер) однією з непозначених вершин.

Крок 1. Отримати двійкове подання числа С та сформувати підмножини N1 та N2, використовуючи значення позицій двійкового числа як позначки для сортування непозначених вершин. Скласти перелік ребер наступного перерізу й визначити його пропускну здатність Вi (N1, N2) як суму пропускних здатностей ребер bij, де i∈N1; j∈N2.

Крок 2. Збільшити значення С на одиницю. Якщо С є більшим ніж 2 (n-2), перейти до кроку 3, інакше – до кроку 1.

Крок 3. Серед отриманих значень {Вi (N1, N2)} вибрати найменше.

Розглянемо приклад, що ілюструє роботу алгоритму.

Нехай потрібно оцінити пропускну здатність між джерелом s та стоком t у неорієнтованій мережі, модель і матрицю пропускних здатностей ребер якої наведено на рисунку 6.13.

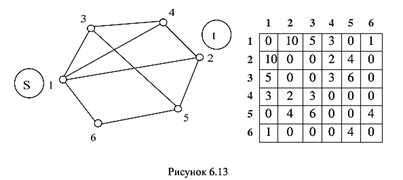
Нехай вершина 1 є джерелом s та позначена як «0», а вершина 2– стоком t та позначена як «1».

Комбінації позначок інших вершин у вигляді двійкових чисел для всіх можливих перерізів і величини їх пропускних здатностей зведено в таблиці 6.1.

Так, наприклад, двійкове подання числа нуль дає змогу сформувати такі підмножини вершин: N1 = (1, 3, 4, 5, 6);

N2 = (2). Список ребер, які мають ненульову вагу, відповідного перерізу: (1,2), (4,2), (5,2). Сумарна пропускна здатність цих ребер дорівнює 16.

Наступному перерізу відповідають розбиття N1 = (1, 3, 4, 5) та N2 = (2, 6), ребра з ненульовою вагами: (1,2), (1,6), (4,2), (5, 2), (5,6) (4,2), (5,2), (5,6) та пропускна здатність, яка дорівнює 21.

За даними таблиці 6.1, найменшу величину пропускної здатності має переріз під номером 0. Вона в даному випадку і визначає пропускну здатність між вершинами s та t у заданій мережі.

Для розв’язання задач про потоки мережі (зважені графи) можуть бути класифіковані відповідно до типу породжуваних потоків. Наведемо означення, необхідні для подальшого засвоєння інформації.

О з н а ч е н н я 6. Мережу, яка має одне джерело та один стік, називають двополюсною.

О з н а ч е н н я 7. Мережу, в якій кожну пару вершин можна розглядати як джерело та як стік, називають багатополюсною.

О з н а ч е н н я 8. Якщо в мережі є декілька джерел і кілька стоків, а потік може йти з будь-якого джерела в будьякий стік, то такий потік називають однопродуктовим (наприклад, мережі газопроводів, нафтопроводів, енергомережі та ін.).

О з н а ч е н н я 9. Якщо в мережі з декількома джерелами та стоками потік повинен іти з деяких виділених джерел до деяких фіксованих стоків, то такий потік називають багатопродуктовим (наприклад, мережі інформаційного зв'язку, мережі перевезень поштових відправлень).

У задачах про багатопродуктові потоки, на відміну від однопродуктових, можна виявити ряд істотних відмінностей.

Наприклад, відомо, що ребро (i, j) завжди можна замінити двома дугами з протилежно направленими стрілками, (i, j) та (j, i). Якщо по цих дугах переміщуються рівні за величиною дугові потоки однопродуктового потоку, то можна стверджувати, що в ребрі (i, j) потік відсутній. Немає сенсу переміщати продукт з пункту i до пункту j у тому випадку, якщо той же самий продукт та з такою ж кількістю переміщується з пункту j в пункту i.

Знаходження максимального однопродуктового потоку в багатополюсній мережі ґрунтується на методах вирішення так званих "транспортних задач".

Інакше відбувається у багатопродуктових потоках. Два рівних за величиною різнопродуктових потоки, які переміщуються по одному ребру в протилежних напрямках не знищують один одного. Ця особливість є прикметною, зокрема, для потоків інформації в телекомунікаційних мережах. Саме це викликає значні труднощі у розв’язанні задач для мереж з багатопродуктовими потоками.

Визначення максимального багатопродуктового потоку в мережі точними методами поки не відбулося, а, отже, зводиться до побудови плану розподілення потоків за допомогою евристичних алгоритмів.

9. Поняття технології в телекомунікаціях. Загальний огляд телекомунікаційних технологій, що забезпечують синхронний режим перенесення інформаційних повідомлень в мережі.

Поняттям «технологія» (Technology) у сфері телекомунікацій позначають спосіб реалізації режиму перенесення інформації в мережі, який забезпечує користувачів певним гарантованим рівнем якості обслуговування.

Термін «режим перенесення» (Transfer Mode) узагальнено розуміють як сукупність методів мультиплексування, передавання та комутації, за допомогою яких у телекомунікаційній мережі уможливлюється транспортування інформації з кінця в кінець, тобто від джерела до одержувача.

Синхронний режим перенесення (Synchronous Transfer Mode) ґрунтується на принципі синхронного часового мультиплексування та часового розділення каналів у процесі передавання інформації від одного вузла комутації до іншого.

При цьому всі ланки тракту передавання інформації з кінця в кінець працюють синхронно. Таку синхронізацію забезпечують спеціальні синхронні технології, основані на використанні генераторів тактових сигналів, які працюють від єдиного еталонного джерела в мережі.

Date: 2016-07-22; view: 607; Нарушение авторских прав