Синтез зв'язувальної мережі мінімальної вартості

Ситуація, в якій деяку множину точок необхідно поєднати так, щоб кожна пара точок стала зв’язною (безпосередньо або через інші точки), а загальна вагова характеристика зв'язків виявилася мінімальною, спонукає до розв’язування задачі синтезу мережі мінімальної вартості. Наприклад, є ряд точок, у яких можуть бути розташовані пункти телекомунікаційної мережі. Відомо: відстані між парами точок і вартість прокладання одного кілометра лінії зв'язку. Необхідно визначити сукупність ліній зв'язку, які забезпечують зв'язність усіх пунктів мережі й мінімальну сумарну вартість їх прокладки. З теорії графів і мереж відомо, що рішенням поставленого завдання є мережа з топологією фізичних зв'язків типу "дерево", тобто такого графа, в якому відсутні цикли.

Кажуть, що граф містить цикли, якщо в ньому можна відшукати замкнуті контури. Відсутність циклів визначає особливість графа типу “дерево”, яка полягає в тому, що між будь-якою парою його вершин існує лише один єдиний шлях їх сполучення, тобто параметр зв'язності h=1. Кількість ребер у дереві є завжди на одиницю меншою від кількості його вершин.

О з н а ч е н н я. Граф типу “дерево”, в якому для кожної пари вершин існує шлях, який їх з’єднує, називають покривним деревом.

Математично задача синтезу мережі мінімальної вартості зводиться до знаходження мінімального покривного дерева. Цю задачу формулюють наступним чином.

Нехай задано неорієнтований граф G(N,V), де множині вершин N відповідає множина пунктів мережі, загальне число яких дорівнює n, а множина ребер V – відстаням {lij} між парами пунктів.

Відома вартість Сij організації одиниці довжини (наприклад, одного кілометра) лінії зв'язку між пунктами i та j.

Необхідно знайти деяке покривне дерево G'(N,V'), для якого досягається мінімум цільової функції:

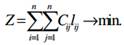
Алгоритм Пріма можна реалізувати шляхом надання позначок вершинам, які вводяться в відшукуваний граф G'(N,V'), і послідовного введення в нього мінімальних за вагою ребер. При цьому, як зазначено вище, загальна кількість ребер не повинна перевищувати (n-1) і між усіма n вершинами покривного дерева має бути зв'язність.

Надамо процедуру виконання алгоритму Пріма у покроковій формі.

Крок 0. Мережа G'(N,V'), яку треба визначити, початково містить n вершин і не має ребер. Вибирають одну довільну вершину i та позначають як "вибрану". Решта (n-1) вершин є "невибраними".

Крок 1. Відшукують ребро (i,j), яке належить G(N,V) з мінімальною вагою, у якого вершина i належить підмножині "вибраних" вершин, а вершина j – підмножині "невибраних" вершин.

Крок 2. Ребро (i,j) розміщують у мережі G'(N,V'), яку треба визначити, а вершину j, вилучаючи з підмножини "невибраних", розташовують у підмножині "вибраних" вершин.

Якщо підмножина "невибраних" вершин виявилася порожньою, то роботу алгоритму завершено. Інакше – перехід до кроку 1.

Проілюструємо роботу алгоритму Пріма на прикладі.

Задано сім пунктів мережі, відстані між якими зведено в матрицю L=||lij||, а саме:

На кроці 0 граф G '(N, V'), який треба знайти, містить сім вершин і не містить ребер. Вибираємо вершину 3 та позначаємо її як “вибрану” (рис. 6.4).

На кроці 1 вибираємо ребро (l35) як ребро з найменшою вагою, у якого вершина i= 3 належить підмножині "вибраних" вершин (воно поки що містить лише одну вершину 3), а вершина j=5 – підмножині "невибраних" вершин (зараз це всі інші вершини). На кроці 2 ребро l35 уводимо у шуканий граф G', а вершину 5 вилучаємо з підмножини "вибраних" вершин (рис. 6.5.).

Оскільки підмножина "невибраних" вершин – порожня, повторюємо крок 1. Для цього знаходимо ребро мінімальної ваги, перебираючи сполучення кожної пари "вибраної" та "невибраної" вершин. Таким виявилося ребро l34 (рис. 6.6), яке розміщуємо у графі G. Вершина 4 стає "вибраною"

Наступними вибираємо ребра: l24 (рис. 6.7); l26 (рис. 6.8);

l13 (рис. 6.9); l27 (рис. 6.10). На цьому робота алгоритму закінчується, тому що всі вершини позначено як "вибрані" (тобто підмножина "невибраних" вершин стала порожньою).

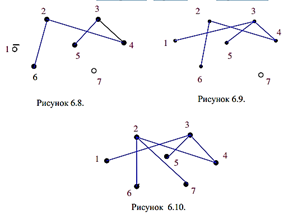
Знайдено відшукуваний граф G'(N,V'), який є покривним деревом, тому що він містить усі вершини, а число ребер на одиницю є меншим кількості вершин (n = 7, v = 6) та забезпечує зв'язність кожної пари вершин.

Знаходження мінімального покривного дерева є однією з класичних задач оптимізації на графах і мережах, оригінальні розв’язування якої запропоновано багатьма авторами. Так, не менш відомим і, до того ж, більш ефективним, з урахуванням швидкості обчислень, є алгоритм, запропонований Краскелом.

Алгоритм Краскела відрізняється тим, що ребра в ньому проглядають у порядку зростання ваг і лиш одноразово.

Звісно, це передбачає виконання попередньої процедури впорядкування ребер у порядку збільшення їх вагових характеристик. У разі однакових ваг ребра розташовують довільно.

Ідея алгоритму ґрунтується на процесі «фарбування» ребер і формуванні «букетів» із вершин. Пояснимо цю ідею.

Для фарбування ребер, які формуватимуть мінімальне покривне дерево, використовуємо, наприклад, зелений колір, а для тих, що поза ним – помаранчевий. Якщо чергове незабарвлене ребро, взяте з упорядкованого списку, не утворює цикл з ребрами зеленого кольору, його забарвлюємо у зелений колір, а з його вершини утворюємо «букет» вершин мінімального покривного дерева, яке будується. Інакше – ребро забарвлюємо у помаранчевий колір. Ребро може утворювати цикл у мінімальному покривному дереві лише в тому випадку, коли його вершини належать до одного «букету». Якщо ж вершини належать різним «букетам», то ребро забарвлюють в зелений колір, а букети зливаються.

Процедуру завершують, коли кількість зелених ребер досягає (n-1), або коли всі ребра будуть, не зважаючи на колір, пофарбованими. Сформулюємо процедуру алгоритму Краскел а покроково.

Крок 0. Упорядкувати ребра за збільшенням ваги. Усі ребра є непофарбованими. Букети відсутні. Вибрати перше з упорядкованого списку ребро (воно має мінімальну вагу), пофарбувати його в зелений колір і сформувати з його вершин перший букет.

Крок 1. Вибрати наступне за списком незабарвлене ребро. Можливим є один із таких варіантів:

а) обидві вершини належать одному букету – пофарбувати ребро в оранжевий колір;

б) одна з вершин належить букету, а інша ні – пофарбувати ребро в зелений колір, вершину долучити до того ж букет;

в) обидві вершини не належать жодному букету – пофарбувати ребро в зелений колір і сформувати з його вершин новий букет;

с) вершини належать різним букетам – пофарбувати ребро в зелений колір, а обидва букета об'єднати в один.

Перейти до кроку 2.

Крок 2. Якщо кількість зелених вершин дорівнює (n-1), або всі вершини пофарбовано – кінець роботи алгоритму.

Інакше – повернутися до кроку 1.

Date: 2016-07-22; view: 558; Нарушение авторских прав