
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Магнитное поле машины
|
|
Электромеханическое преобразование энергии происходит в воздушном зазоре электрической машины — в пространстве, где сосредоточена энергия магнитного поля. Поэтому изучение магнитного поля машины имеет важное значение для понимания процессов преобразования энергии в электрических машинах. Магнитное поле машины создается токами, протекающими в обмотках машины. На формирование поля оказывает определенное влияние окружающая среда.
Для развития теории электрических машин имели решающее значение работы М. Фарадея и его физические представления о магнитном поле. М. Фарадей представлял магнитное поле как пространство, заполненное магнитным потоком, который состоит из замкнутых силовых линий. При этом деформации, тяжения силовых линий создают пондеромоторные (электродинамические) силы, которые непосредственно участвуют в электромеханическом преобразовании.
В основе уравнений электромеханического преобразования энергии лежат работы Д. Максвелла, который облек в математическую форму представления М. Фарадея.
По магнитной индукции и напряженности поля электрической машины можно определить параметры и другие показатели, интересующие исследователя. Однако расчет поля машины может быть проведен только приближенно. Определение параметров и характеристик электрических машин требует большого времени ЭВМ, и в настоящее время используются только частичные программы для расчета отдельных показателей машины.
На рисунке 1.45 представлено распределение магнитных потоков в четырех полюсном асинхронном двигателе при нагрузке. Силовые линии поля деформируются и распределяются в участках магнитной системы неравномерно. Картина поля на одном полюсном делении явнополюсной синхронной машины представлена на рисунок 1.46.
Картина поля в машине зависит от нагрузки приложенного напряжения, режима работы и геометрии магнитной системы. Форма поля непрерывно изменяется, отражая все события, происходящие в машине.
Расчет магнитного поля состоит из определения плотности магнитного потока, т. е. магнитной индукции — вектора, направление которого в каждой точке поля совпадает с направлением силовых линий поля (рисунок 1.46).

 Из уравнений Максвелла для магнитного поля вектор напряженности равен
Из уравнений Максвелла для магнитного поля вектор напряженности равен
rot
H = J
(1.15)
Считая, что плотность тока J равномерно распределена по сечению проводника S, имеем
 J = I
J = I
S
(1.16)
Связь между индукцией и напряженностью поля определяется зависимостью


|
|
(1.17)

Рисунок 1.45. Магнитное поле четырехполюсного асинхронного двигателя при
Нагрузке

Рисунок 1.46. Магнитное поле явиополюсной синхронной машины
Так как силовые линии магнитного поля замкнуты, то

div B = 0,
(1.18)
что свидетельствует о том, что силовые линии магнитного поля не имеют «стоков» и
«истоков».
Уравнения (1.15) — (1.18) позволяют аналитически найти магнитное поле лишь для ограниченного круга задач с простейшими граничными условиями.
Магнитные поля в электрических машинах значительно сложнее поля, представленного на рисунок 1.47. Обычно в машинах поле концентрируется в воздушном зазоре и в его создании участвуют несколько контуров с токами. Обмотки, как правило, располагаются в пазах, а магнитный поток замыкается как по стали, так и по воздуху, вокруг лобовых частей обмоток.
Для реальных областей электрических машин со сложными формами магнитных сердечников и контуров с токами при расчете поля приходится идти на ряд допущений, связанных с формой поверхностей, с распределением токов, со свойствами сред и законами движения.

Рисунок 1.47. Магнитное поле витка с током

|

|
Для магнитного потенциала справедливо уравнение Лапласа
(1.19)

|
¶2 j
 = m +
= m +
¶2 j
 m +
m +
¶2 j
= 0.
(1.20)
m ¶ x 2
¶ y 2
¶ z 2
В безвихревом магнитном поле в электрических машинах большая часть граничных условий является условиями Дирихле, что облегчает решение при использовании приближенных методов. Результатом расчета поля являются составляющие напряженности поля по трем осям
 H = - ¶ jm;
H = - ¶ jm;
x ¶ x
H = - ¶ jm;
 y ¶ y
y ¶ y
H = - ¶ jm,
 z ¶ z
z ¶ z
(1.21)
по которым с использованием равенства
B = m × H,
находят составляющие вектора
|
При расчете вихревых электромагнитных полей используется понятие векторного
 магнитного потенциала A:
магнитного потенциала A:

 B = rot A.
B = rot A.
(1.22)
Совместное решение (1.15) — (1.17) приводит к уравнению Пуассона


|
(1.23)
Циркуляция векторного потенциала по контуру оказывается равной магнитному потоку через поверхность, опирающуюся на этот контур. Уравнение (1.22) разбивается в трехмерной задаче на три отдельных уравнения, записанных в проекциях на
координатные оси. В электрических машинах обычно рассматривается двухмерная плоскаякартина поля с одной, например, составляющей тока Iz по оси z:
|
 ¶ x 2
¶ x 2
¶2 A

|
¶ y 2
= - m
Jz.
(1.24)
|
 B = ¶ Az;
B = ¶ Az;
x ¶ y
B = ¶ Az.
 y ¶ x
y ¶ x
(1.25)
Для нахождения магнитного поля используются методы подобия, физического и математического моделирования. Значительную роль в решении полевых задач играют конформные преобразования областей решения, при которых сложные граничные условия претерпевают изменения и существенно упрощаются. Решение уравнения Лапласа находится для относительно простых зон и далее переносится в исходную область. Методы конформного преобразования развиты в основном для безвихревых полей. Ряд задач для вихревого поля решается методами интегральных уравнений.
В последние десятилетия быстро развивались приближенные численные приемы расчета поля, основанные на методах конечных разностей и конечных элементов. Быстродействующие ЭВМ дают возможность получить решение при расчете поля машины с затратой сравнительно большого машинного времени. Недостатками этих методов являются невозможность получить общее выражение для решения и необходимость повторять решения при изменении любых факторов, влияющих на поле. Но все возрастающие возможности вычислительной техники компенсируют это неудобство. Усилиями ряда ученых удалось создать метод расчета магнитных полей, в основе которого лежит представление о том, что поле реальной машины можно создать с помощью полей простейших контуров, размещенных на зубцах сердечников. Этот метод получил название метода проводимостей зубцовых контуров.
Электромеханическое преобразование энергии связано с электромагнитными силами и моментами, возникающими в электрических машинах. При определении этих сил может быть несколько подходов.
Механическое, или пондермоторное, взаимодействие токов подчиняется закону Ампера.

 Для проводника с током i, находящегося во внешнем магнитном поле B, электромагнитная сила F определяется векторным произведением
Для проводника с током i, находящегося во внешнем магнитном поле B, электромагнитная сила F определяется векторным произведением


 f = [ l × B ]× i,
f = [ l × B ]× i,
(1.26)

где l — единичный вектор длины провода с током i
Когда в результате применения уравнений Максвелла определено магнитное поле, электромагнитные силы удобно выразить через так называемый тензор натяжения
 n × H 2
n × H 2


|
|
× H - m,

(1.27)
 где
где
H — составляющая вектора напряженности магнитного поля H в направлении орта

|
m — магнитная
Интегрируя тензор натяжения по всем поверхностям, на которых имеет место
существенное значение магнитного поля, можно перейти к значениям электромагнитных сил и момента.
Иногда целесообразно определять электромагнитные силы и моменты из выражения удельной энергии, равной скалярному произведению плотности тока и векторного потенциала стороннего магнитного поля:



 ¶ W = 1 A × J
¶ W = 1 A × J
¶ V 2
= 1 B × H.


 2
2
(1.28)
Следующее важное уравнение Максвелла связывает вектор электрической напряженности Е с магнитной индукцией:
rot


 E = - ¶ B.
E = - ¶ B.
¶ t
(1.24)
(1.29)
В интегральном виде оно позволяет перейти к выражению для ЭДС контура
 æ ¶ ö
æ ¶ ö



 E = ò - ç
E = ò - ç
B ÷ dS +
ò[ V × B ]
dl.
(1.30)

|
Векторы магнитной индукции и напряженности дают исчерпывающую информацию о магнитном поле и, следовательно, обо всех интегральных величинах (токах, ЭДС, напряжениях, силах и моментах) на выводах машины. Наиболее существенным параметром является индуктивность L, вычисляемая как отношение мгновенных значений потокосцепления Ψ, созданного током i, к самому току:
 L = Y.
L = Y.
i
(1.31)
Если ток и потокосцепление принадлежат одной и той же обмотке или проводнику, индуктивность называется самоиндуктивностью, если разным — взаимной индуктивностью. Для поля, описываемого уравнением Лапласа, в целях нахождения потокосцепления приходится переходить к выражению магнитной индукции и далее интегрировать для проводника сечением S магнитные потоки в пределах сечения. В терминах векторного магнитного потенциала потокосцепление определится относительно значенияА0, принимаемого за начало отсчета текущих значений векторного потенциала Ai,имеющих место в сечении S:

|
(1.32)
ò i 0
S
Практически определение потокосцепления сводится к простейшим арифметическим операциям, если проводник разделяется на конечное число элементарных площадок, для каждой из которых при расчете поля установлено значение векторного магнитного потенциала Ai.
Потокосцепление проводника или обмотки с числом витков w в том случае, когда поток Ф для всех точек поперечного сечения проводника обмотки является постоянным, может быть вы ражено как Y = w ×Ф, и тогда индуктивность

 L = Y = w ×F.
L = Y = w ×F.
(1.33)
i i
Введем понятие магнитной проводимости L:
 L = F,
L = F,
F
где F — МДС проводника (обмотки).
(1.34)
Индуктивность теперь оказывается величиной, не зависящей от значений тока и потока, и определяется только значением магнитной проводимости

 L = w × F ×L = w × i × w ×L = w 2 L,
L = w × F ×L = w × i × w ×L = w 2 L,
(1.35)
i i
В случаях, когда имеются воздушные промежутки,
L = w L = w m l,
(1.36)
—коэффициент магнитной проводимости для потоков, созданных МДС F.
Результирующее поле машины принято делить на магнитное поле взаимной индукции и поле рассеяния. Для представленного на рисунок 1.48 варианта двух обмоток силовые линииполя взаимной индукции сцеплены с обеими обмотками Ф12, а силовые линии поля рассеяниясцепленытолько с одной обмоткой (F s 1 —поле рассеяния первичной обмотки w 1, F s 2 —поле рассеяния вторичной обмотки w2).

Рис. 1.48, Магнитные поля взаимной индукции и поля рассеяния
При конструировании электрических машин стремятся к тому, чтобы большая часть потока была сцеплена с обеими обмотками, расположенными на статоре и роторе, а потоки рассеяния составляли несколько процентов потока взаимной индукции. Хотя процессы электромеханического преобразования энергии определяются результирующим полем, основное значение имеет поле взаимной индукции или главное поле машины.
При расчете поля взаимной индукции часто используется допущение о плоскопараллельности (двухмерности) поля, когда не учитывается изменение формы поля в направлении оси z, а также широко применяется принцип наложения.
Связь между индукцией В и токами, создающими поле, определяется законом полного тока. Поэтому интеграл вектора напряженности магнитного поля по замкнутому контуру равен полному току, проходящему сквозь этот контур:
Bl


|
a
dl = å ik,
(1.37)

 где
где
Hl,
Bl — проекции векторов напряженности поля H и индукции B на направление
обхода контура dl. Когда контур интегрирования совпадаете направлением силовых линий
поля, Hl
B).
и Bl
равняются напряженности и индукции в данной точке (соответственно Н и
Интеграл по замкнутому контуру в (1.35) вычисляют по участкам, на которые разбивают контур интегрирования. Линейный интеграл какого-либо участка ò Hldl называется МДС этого участка.
Расчет магнитной цепи проводят при холостом ходе, когда ток в обмотке якоря близок или равен нулю.
Магнитную цепь явнополюсной (рисунок 1.49, а) и неявнополюсной (рисунок 1.49, б)
машин разбивают на пять участков:
å F = Fd + Fz + Fm + Fa + Fc,
(1.38)
где Fd
— МДС воздушного зазора (участки 3 — 4, 9 — 10); Fz
— МДС зубцов (участки 2 —
3, 8—9, 10 — 11); Fm — МДС полюса (участок 4—5); Fa — МДС ярма ротора (участки 1 —
2, 7—5); Fc — МДС ярма статора (участки 5-6, 11-12).

Рисунок 1.49, Магнитная система явнополюсной (а) и неявнополюсной (б) машин
При расчете МДС участков явно- и неявнополюсных машин с обмоткой возбуждения на статоре и роторе явнополюсных машин имеются особенности в расчетах, которые рассматриваются в соответствующих разделах курса.
МДС зазора Fd
расчитывается как
Fd = kd
× Hd × d
(1.39)
где Hd
— напряженность воздушного зазора,
H = (B / m);
Fd = kd × Hd × d
—длина
|
|
— коэффициент воздушного зазора, учитывающий увеличение
длины силовой линии поля в воздушном зазоре за счет пазов, Магнитодвижущая сила зубцов
kd = 1,1-1,5.
Fz = Hz × lz
(1.40)
где Hz
— средняянапряженностьмагнитногополяв зубце; lz
— высота зубца.
Средняя напряженность вычисляется по значениям индукции в трех сечениях зубца. Если
индукцияв зубце не изменяется, то Hz
определяется для всей длины зубца.
Магнитодвижущая сила полюса рассчитывается по формуле
Fm = Hm × lm
(1.41)
здесь Hm
— напряженность в полюсе;
Fm = Hm × lm — длина полюса.
Магнитодвижущая сила ярма ротора
Fa = Ha × la
(1.42)
где
Ha — напряженность в ярме ротора; la
— длина силовой линии в ярме ротора
машины.
Магнитодвижущая сила ярма статора
Fc = Hc × lc
(1.43)
где Hc
— напряженность в ярме статора; lc — длина силовой линии в ярме статора.
В неявнополюсных сердечниках МДС ярм статора и ротора рассчитывается с учетом коэффициента влияния на МДС неравномерности распределения индукции в ярмах статора и ротора машины:
Fa = x × Ha × la
(1.44)
При расчете магнитной цепи машины задаются индукцией в воздушном зазоре
Bd, а
затем, определив поток, рассчитывают индукцию на остальных участках при известной геометрии машины. Вычислив значения индукции в отдельных участках, по таблицам для соответствующего сорта стали определяют напряженность поля для каждого участка.
Просуммировав МДС участков, находят полный ток (1.38):
å F = I × w = F в
(1.45)
где
F в — МДС обмотки возбуждения.
Расчет МДС проводят для нескольких значений
Bd, а затем строят характеристику
намагничиваниямашиныили магнитную характеристику машины Фd
= f (F в)
(рисунок
1.50). Начальная часть характеристики соответствует ненасыщенному состоянию и
определяетсязависимостью Фd
= f (Fd), так как МДС участков магнитопроводов малы.
 Рабочая точка, соответствующая номинальному значению потока в зазоре выбирается на колене магнитной характеристики.
Рабочая точка, соответствующая номинальному значению потока в зазоре выбирается на колене магнитной характеристики.
Fd ном,
Рисунок 1.50, Магнитная характеристика машины
Обычноå F рассчитываютна пару полюсов. При этом в контур, где замыается поток, входят два воздушных зазора, две длины зубцов, полюсов и полные длины силовых линий в ярмах статора и ротора (см. рисунок 1.49). После расчета магнитной системы можно определить МДС сосредоточенной обмотки возбуждения на один полюс
I в× w в
= F в
2
(1.46)
где
I в —ток возбуждения;
w в— число витков обмотки возбуждения.
В многополюсных машинах картина поля повторяется под каждой парой полюсов, поэтому расчет магнитной системы проводят на пару полюсов.
Магнитодвижущую силу машины можно представить в следующем виде (рис. 1.39):
å F = Fd
+ F ст
(1.47)
|
|
|
+ F ст
)/ F
(1.48)
определяет коэффициент насыщения машины, который зависит от воздушного зазора и
насыщения стальных участков магнитной цепи машины,
k н» 1,1-1,6.В синхронных
машинах и машинах постоянного тока
k н» 1,1-1,3, а в асинхронных
k н» 1,2-1,6. Выбор
индукций в зазоре и зубцах определяет энергетические и массогабаритные характеристики машины.
|
|
магнитную проницаемость стали
зазоре пропорциональна I·w:
ст то при этом FCT равнанулюи индукция в
 B = m 0 I × w = k × I × w
B = m 0 I × w = k × I × w
d d ¢
(1.49)
где d ¢ = kd × d.
В ненасыщенной машине форма поля в зазоре при холостом ходе определяется распределением МДС обмотки, в которой протекает ток намагничивания, и магнитным сопротивлением воздушного зазора (рисунок 1.51).

Рисунок 1.51, Магнитное поле неявнополюсной машины
В неявнополюсной машине с равномерным зазором и гладкими статором и ротором (пазы на статоре и роторе отсутствуют) форма поля в воздушном зазоре определяется распределением МДС обмотки.
Синусоидальное распределение индукции в зазоре ненасыщенной неявно- полюсной машины можно получить при синусоидальном распределении МДС, что теоретически обеспечивается синусными обмотками, в которых витки распределяются по закону синуса.
В явнополюсных ненасыщенных машинах с обмотками возбуждения в виде сосредоточенных катушек форма поля в зазоре определяется магнитным сопротивлением воздушного зазора. Чтобы приблизить форму поля в зазоре к синусоиде, надо профилировать зазор следующим образом (рисунок 1.52):
|
|

|
 cos x
cos x
t
(1.50)
где d — зазор под серединой полюса.

Рисунок 1.52, Профиль воздушного зазора явнополюсной машины
При этом зазор под краем полюсного наконечника получается равным (1,5-1,6) δ.
Хотя в явнополюсной машине, имеющей неравномерный воздушный зазор, выполненный по (1.50), поле в зазоре имеет трапецеидальную форму, высшие гармоники имеют
небольшие амплитуры. На рисунок 1.53 В1тах — амплитуда 1-йгармоники,Вδср среднеезначениеиндукциив воздушном зазоре. При расчетах электрических машин Вδср входитв формулы для определения ЭДС.

Рисунок 1.53. Магнитное поле явнополюсной машины
Зубцы на статоре изменяют магнитное сопротивление воздушного зазора и вносят искажения в форму поля в воздушном зазоре (рисунок 1.54). Наличие пазов на роторе и статоре еще более усложняет картину поля. Однако амплитуда 1-й гармоники при этом изменяется мало.
При нагрузке поле взаимной индукции определяется токами, протекающими в обмотках статора и ротора. При этом происходит искажение формы поля в воздушном зазоре и поток в зазоре Фδ уменьшаетсяпо сравнению с потоком при холостом ходе. Влияние тока нагрузки на характеристики машины называют реакцией якоря. Реакция якоря в различных типах машин проявляется по-разному и изучается в соответствующих разделах курса.
Поле рассеяния машины делят на три части: на поле пазового рассеяния, поле рассеяния лобовых частей и поле дифференциального рассеяния.
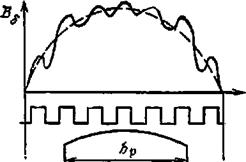
Рисунок 1.54. Поле машины при наличии пазов на статоре
Поле пазового рассеяния делится на поле рассеяния в пазу и поле рассеяния по головкам зубцов(рисунок1.55). Поток пазового рассеяния зависит от геометрии паза (bп — высоты и hп — ширины паза), а также от размера раскрытия (шлица) паза b ш и высоты усика паза hш. Расчетполя пазового рассеяния осложняется наличием токов в пазу и сложной формой пазоз, поэтому аналитические решения возможны лишь для простейших случаев и при проектировании используются приближенные соотношения, полученные из опыта изготовления и эксплуатации электрических машин.
Рассеяние лобовых частей обмоток зависит от выполнения лобовых частей числа полюсов и вида обмотки. Обычно лобовое рассеяние меньше пазового.
В воздушном зазоре электрической машины наряду с основной гармоникой поля существуют поля высших гармоник. При расчете электрических машин рабочим потоком считают поток 1-й гармоники, а потоки высших гармоник поля относят к потокам рассеяния воздушного зазора или дифференциальному рассеянию.

Рисунок 1.55. Поле пазового рассеяния
2) НАЗНАЧЕНИЕ И ОБЩИЕ СВЕДЕНИЯ О ТРАНСФОРМАТОРАХ
Трансформаторы — электромагнитные статические преобразователи электрической энергии. Основное назначение трансформаторов — изменять напряжение переменного тока. Они применяются также для преобразования числа фаз и частоты. Наибольшее распространение имеют силовые трансформаторы напряжения, которые выпускаются электротехнической промышленностью на мощности свыше миллиона киловольт- ампер и на напряжения до 1150—1500 кВ.
Для передачи и распределения электрической энергии необходимо повысить напряжение турбогенераторов и гидрогенераторов, установленных на электростанциях, с 16—24 кВ до напряжений 110, 150, 220, 330, 500, 750 и 1150 кВ,
используемых в линиях передачи, а затем снова понизить до 35; 10; 6; 3; 0,66; 0,38 и 0,22 кВ, чтобы использовать энергию в промышленности, сельском хозяйстве и быту. Так как в энергетических системах имеет место многократная трансформация, мощность трансформаторов в 7—10 раз превышает установленную мощность генераторов на электростанциях. Силовые трансформаторы в СССР выпускаются в основном на частоту 50 Гц.
Трансформаторы малой мощности широко используются в различных электротехнических установках, системах передачи и переработки информции, навигации и других устройствах. Диапазон частот, на которых могут работать трансформаторы, — от нескольких герц до 105Гц,
По числу фаз трансформаторы делятся на однофазные, двухфазные, трехфазные и многофазные. Силовые трансформаторы выпускаются в основном в трехфазном
исполнении. Для применения в однофазных сетях выпускаются однофазные трансформаторы.
Трансформаторы имеют две или несколько обмоток, индуктивно связанных друг с другом. Обмотки, потребляющие энергию из сети, называются первичными. Обмотки, отдающие электрическую энергию потребителю, называются вторичными.
Многофазные трансформаторы имеют обмотки, соединенные в многолучевую звезду или многоугольник. Трехфазные трансформаторы имеют соединение в трехлучевую звезду и треугольник.
В зависимости от соотношения напряжений на первичной и вторичной обмотках трансформаторы делятся на повышающие и понижающие. В повышающем трансформаторе первичная обмотка имеет низкое напряжение, а вторичная — высокое. В понижающем трансформаторе, наоборот, вторичная обмотка имеет низкое напряжение, а первичная — высокое.
Трансформаторы, имеющие одну первичную и одну вторичную обмотки, называются двухобмоточными. Достаточно широко распространены трехобмоточные трансформаторы, имеющие на каждую фазу три обмотки, например две на стороне низкого напряжения, одну — на стороне высокого напряжения или наоборот. Многофазные трансформаторы могут иметь несколько обмоток высокого и низкого напряжения.
По конструкции силовые трансформаторы делят на два основных типа — масляные и сухие. В масляных трансформаторах (рисунок 2.1) магнитопровод с обмотками находится в баке, заполненном трансформаторным маслом, которое является хорошим изолятором и охлаждающим агентом. Сухие трансформаторы охлаждаются воздухом. Они применяются в жилых и промышленных помещениях, в которых эксплуатация масляного трансформатора является нежелательной (рисунок 2.2). Трансформаторное масло является горючим, и при нарушении герметичности бака масло может повредить другое оборудование.

Рисунок 2.1. Трехфазный трансформатор ТЦ- 1000000/500 мощностью 1 млн. кВ А,
Напряжением 500 кВ

Рисунок 2.2. Взрывобезопасный трансформатор ТСВ-160/6 мощностью 160 кВ А, напряжением 6 кВ
Наряду с трансформаторами широко применяются автотрансформаторы, в которых имеется электрическая связь между первичной и вторичной обмотками. При этом мощность из одной обмотки в другую передается как магнитным полем, так и за счет электрической связи. Автотрансформаторы строятся на большие мощности и высокие напряжения и применяются в энергосистемах, а также используются для регулирования напряжения а установках небольшой мощности.
Номинальные данные трансформатора, на которые он рассчитан с заводской гарантией на 25 лет указываются в паспортной табличке трансформатора: номинальнаяполнаямощность Sном,кВ·А,номинальноелинейноенапряжение Uл_ном, В или кВ, номинальный линейный ток Iл_ном А,номинальнаячастота f,Гц,числофаз т, схемаи группа соединения обмоток, напряжение короткого замыкания Uk, %,режим работы, способ охлаждения. В табличке приводятся также данные, необходимые для монтажа:полная масса, масса масла, масса выемной (активной) части трансформатора. Указываются тип трансформатора в соответствии с ГОСТ на марки трансформаторов и завод-изготовитель.
 Номинальная мощность однофазного трансформатора
Номинальная мощность однофазного трансформатора
Sном = U 1_ ном × I 1_ ном, а
трехфазного
Sном =
3 × U 1 л _ ном × I 1 л _ ном = 3× U 1 ф _ ном × I 1 ф _ ном, где U 1 л _ ном, I 1 л _ ном, U 1 ф _ ном и
I 1 ф _ ном
токов.
- соответственно номинальные линейные и фазные значения напряжений и
Номинальными напряжениями трансформатора являются линейные напряжения при холостом ходе на первичной и вторичной обмотках трансформатора. За номинальные токи первичной и вторичной обмоток принимаются токи, рассчитанные по номинальной мощности при номинальных первичных и вторичных напряжениях.
Ввиду общности конструкции и методов расчета к трансформаторам могут быть отнесены реакторы, дроссели насыщения и сверхпроводящие индуктивные накопители. Большая группа электромагнитных устройств, применяемых в системах автоматического управления, — магнитные усилители, различные датчики, измерительные трансформаторы — хотя и имеет общие уравнения с силовыми трансформаторами, рассматривается в других курсах.
3) РАБОТА АСИНХРОННОГО ДВИГАТЕЛЯ ПРИ НЕСИНУСОИДАЛЬНОМ НАПРЯЖЕНИИ
В схемах частотного регулирования, когда асинхронный двигатель получает питание от статического преобразователя частоты, к обмоткам двигателя подводится несинусоидальное напряжение прямоугольной формы (см. рис. 4.45, б). Анализ особенностей работы асинхронного двигателя от несинусоидального напряжения обычно проводят, разлагая заданную форму кривой напряжения в гармонический ряд и исследуя отдельно действие каждой гармонической. При указанной форме подведенного к фазе напряжения гармонический ряд не содержит четных гармонических:
(4.76)
u = 4U [sin ωt + (1/3) sin 3ωt + (1/5) sin 5ωt +...]/π
Высшие гармонические питающего напряжения обусловливают появление высших гармонических тока и магнитного потока, вследствие чего возникают дополнительные потери в обмотках и стали магнитопровода. Кроме того, наличие высших гармонических приводит к появлению вращающих и тормозящих моментов от взаимодействия токов и потоков одного порядка, а также колебательных моментов от взаимодействия между собой гармонических разных порядков.
Магнитное поле. Каждая гармоническая напряжения создает магнитное поле, вращающееся с частотой
(4.77)
n1v = 60fv /p = (60f1 /p) v = n1 v.
Исключение составляют третья гармоническая и другие, кратные трем, которые создают пульсирующее поле, так как МДС указанных гармонических во всех трех обмотках статора совпадают по времени. Если преобразователь частоты обеспечивает сдвиг по фазе между первыми гармоническими напряжения трех фаз α1 = 120°, то для высших гармонических этот сдвиг αv = 120°v. Однако для третьей гармонической α3 = 360°, что равносильно отсутствию сдвига по фазе. Различие в сдвигах по фазе приводит к тому, что направления вращения магнитных полей, созданных высшими гармоническими тока, различны, так как у них различно чередование максимума токов в фазах. Например, для пятой гармонической α5 = 120° • 5 = 600° = 2 • 360° — 120°, т. е. чередование максимумов тока в фазах является обратным по сравнению с чередованием токов первой гармонической. Следовательно, пятая гармоническая магнитного потока вращается в сторону, противоположную направлению вращения основного магнитного поля (поля первойгармонической).Для седьмой гармонической α7 = 120° • 7 = 840° = 2 • 360° + 120° чередование максимумов тока, а следовательно, и направление вращения поля совпадают с первой гармонической.
В табл. 4.1 приведены данные для магнитных полей высших гармоник, вычисленные до 25-й гармоники включительно.
Таблица 4.1
| Номер гармоничес кой | Амплиту да | Направле ние вращения | Скольже ние Sv при S1 = 0 | Номер гармоничес кой | Амплиту да | Направле ние вращения | Скольже ние SvприS1 = 0 |
| + | 0.066 | - | |||||
| 0.333 | - | 0.059 | - | 1.06 | |||
| 0.200 | - | 1.2 | 0.052 | + | 0.95 | ||
| 0.143 | + | 0.86 | 0.047 | - | |||
| 0.111 | - | 0.043 | - | 1.04 | |||
| 0.091 | - | 1.09 | 0.040 | + | 0.96 | ||
| 0.077 | + | 0.92 |
Знаком «+» показано совпадение направления вращения поля высшей гармонической с первой, знаком «-» - обратное направление вращения, знаком «0» — неподвижное поле (для третьей гармонической и гармонических, кратных трем).
Наиболее опасной является третья гармоническая напряжения, так как она имеет максимальную амплитуду и сравнительно небольшую частоту. Поэтому во всех устройствах частотного регулирования необходимо устранение третьей гармонической тока путем применения специальных реакторов или соединения обмоток двигателя по схеме Y, что исключает прохождение совпадающих во времени третьих гармонических тока.
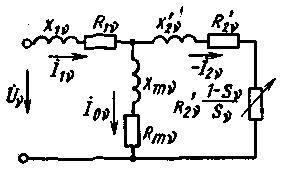
Схема замещения. Расчет действия высших гармонических (с 5-й и выше, кроме кратных трем) целесообразно проводить по схеме замещения асинхронного двигателя (рис. 4.52).
Скольжение для высших гармонических можно определить по формуле (4.78)
sv = (nv ± n2)/nv = [(vn1 ± n1 (1- s1)]/vn1 = [v ± (1 - s1)]/v.
Поскольку при номинальном режиме работы скольжение для первой гармонической невелико(s 1ном = 0,02÷0,05), приближенное значение s v (при s 1 =0):
(4.78a)
sv ≈ (v ± 1)/v = 1 ± 1/v.
Очевидно, что знак «+» в формуле (4.78 а) соответствует отрицательному направлению поля высшей гармонической. Значения sv, подсчитанные по формуле (4.78 а), приведены в табл. 4.2. Данные таблицы показывают, что в первом приближении скольжение для высших гармонических может быть принято равным единице. Индуктивные сопротивления X vl и X 'v2,обусловленныепотокамирассеяния,пропорциональнычастотеи берутся кратными номеру гармонической
(4.79)
Xv1 = vX1; X'v2 = vX'2.
Активные сопротивления в машинах небольшой мощности не зависят от частоты: (4.80)
Rv1 = R1; R'v2 = R'2.
Как показывает практика, в машинах средней и большой мощности при высоких частотах происходит довольно интенсивное вытеснение тока, вследствие чего активные сопротивления увеличиваются с возрастанием частоты и их можно определять по формулам, аналогичным для индуктивных сопротивлений:
(4.80a)
Rv1 = vR1; R'v2 = vR'2.
При расчетах высших гармонических токов намагничивающим контуром схемы замещения можно пренебречь в связи с малостью амплитуд напряжений и повышенной частотой. Поэтому ток в рабочем контуре схемы замещения для машин средней и большой мощности
(4.81)
 Iv = Uv /[v√(R1 + R'2)2+ (X1 + X'2)2].
Iv = Uv /[v√(R1 + R'2)2+ (X1 + X'2)2].
Электрические потери в обмотках от токов высших гармонических. Эти потери определяются по схеме замещения (рис. 4.52). Для крупных электрических машин
|
 Δ Pэлv = m1 Iv (Rv1 + R'v2) =
Δ Pэлv = m1 Iv (Rv1 + R'v2) =
+ R'v2) =
(Rv1 + R'v2)2+ (Xv1 + X'v2)2
2 2 2
|
v2[(R1 + R'2)2+ (X1 + X'2)2]
v3[(R1 + R'2)2+ (X1 + X'2)2] v3
где Рк = m1U12(R1 + R'2)/[(R1 + R'2)2+ (X1+X'2)2] - электрические потери в обмотках двигателя в режиме короткого замыкания при номинальном синусоидальном напряжении. Электрические потери в обмотках двигателя при коротком замыкании Рк больше
электрическихпотерь Δ Р эл.номприноминальномрежимеи номинальном синусоидальном напряжении:
Рк / Δ Рэл.ном = (I п /Iном)2= k2 п,
где kп = (Iп /Iном) — отношение пускового тока к номинальному; для машин, работающих при синусоидальном напряжении, k п = 5÷7, а для машин, работающих при прямоугольном напряжении, k п = 3÷5.
Поэтому
(4.82)
Δ Рэлv = k п2Δ Рэл.ном /v3.
 Коэффициент увеличения электрических потерь в двигателе при питании его напряжением прямоугольной формы
Коэффициент увеличения электрических потерь в двигателе при питании его напряжением прямоугольной формы
Рис. 4.52. Упрощенная схема замещения асинхронного двигателя при питании его несинусоидальным напряжением
(4.83a)
kэл =
Δ Pэл.ном
= 1 + k п2(1

|
+ 1 + 1

 73 113
73 113
+ 1
 133
133
+...).
При k п = 3÷5 этот коэффициент (4.83a)
kэл ≈ 1 + k п2 /80 ≈ 1,11÷1,30.
Следовательно, в крупных машинах увеличение электрических потерь может быть довольно существенном и примерно равноценным возрастанию тока на 5 — 15%. Чтобы уменьшить электрические потери, крупные машины, работающие при несинусоидальном напряжении,обычновыполняютна пониженную кратность пускового тока k п = 3÷5, т. е. с увеличенными значениями индуктивных сопротивлений X 1 и X 2. Это, в свою очередь, приводит к снижению перегрузочной способности двигателя. В машинах небольшой мощности электрические потери в обмотках возрастают в меньшей степени так как у них активное сопротивление из-за вытеснения тока увеличивается незначительно. Аналогично предыдущему для них
(4.83б)
k эл ≈ 1 + k п2/500 ≈ 1,02÷1,05.
Магнитные потери в стали от высших гармонических. Обычно магнитные потери невелики, так как амплитуды высших гармонических магнитного потока малы. Поскольку для высших гармонических машина находится в режиме короткого замыкания, приближенноможнопринять,чтоЭДС статора E v ≈ 0,5 U v.Относительное значение потока
(4.84)
Фvm /Ф1m ≈ Ev f1 /(U1 fv) ≈ 0,5 (Uv /U1) (f1 / fv). При прямоугольной форме напряжения (4.84a)
Фvm /Ф1m = 0,5/v2.
В первом приближении магнитные потери в стали можно определить по соотношению (4.85)
 Δ P мv ≈ (Фvm)2(fv)1,5≈ 0,25 v 1,5= 0,25.
Δ P мv ≈ (Фvm)2(fv)1,5≈ 0,25 v 1,5= 0,25.
Δ Pм1
Ф1m f1 v4
v2√v
Магнитные потери в стали от пятой гармонической составляют около 0,5% от основных потерь, от седьмой гармонической — 0,19 % и т. п. Суммарные потери в стали от высших гармонических, определенные по формуле (4.85), не превышают 0,7%. Формула (4.85) не являетсяточной, так как магнитные потери Δ P мv от высших гармонических возникают из-за перемагничивания стали по частичному циклу и имеют примерно в два раза большую величину, чем по формуле; однако это не изменяет вывода о незначительном увеличении потерь в стали.
Вращающие и тормозящие моменты от высших гармонических. Эти моменты рассчитывают так же, как электромагнитный момент от основной гармонической:
(4.86)
Mv = cмФvm I2v cosψ2v,
или (4.87)
|
R'2v /(ωv sv),
где ωv — угловая скорость магнитного поля данной гармони-ческой; sv — скольжение для поля данной гармонической.
Направление момента определяется направлением вращения поля высшей гармонической относительно основного поля — при совпадении направлений этих полей момент вращающий, при несовпадении — тормозной. Из табл. 4.1 видно, что вращающим моментам соответствует s < l; тормозным — s > 1.
Для упрощенной оценки моментов можно положить электрические потери в роторе равными потерям в статоре:
(4.88)
Δ Pэлv2 ≈ 0,5 Δ Pэлv ≈ 0,5k п2Δ Pэл.ном /v3≈ 0,5Pк /v3.
Считая,как и прежде, для высших гармонических sv ≈ 1 и ωv ≈ ω1v,получаем (4.89)
Mv = Δ Pэлv2 /(ωv sv) ≈ Pк /(2v3ω1 v • 1) ≈ Pк /(v4• 2ω1) ≈ М п /v4,
где М п ≈ 0,5 P к /ω1 — пусковой момент от основной гармонической напряжения при тех же условиях (электрические потери в роторе и в статоре одинаковы).
|
В малых машинах, где эффект от вытеснения тока невелик, моменты еще меньше: (4.90)
Mv /M п ≈ 1/[v4÷ v5],
т. е. меньшим машинам соответствуют меньшие значения Mv /M п.
Колебательные моменты. В результате взаимодействия токов одних частот с потоками других возникают знакопеременные моменты, частота которых значительно выше основной частоты, а среднее значение равно нулю. Общее количество колебательных моментов очень велико, так как взаимодействие возникает между всеми гармоническими. Однако колебательные моменты, возникающие от взаимодействия высших гармонических между собой, имеют тот же порядок, что и рассмотренные выше вращающие моменты, т. е. пренебрежимо малы. Практически могут иметь значение лишь колебательные моменты, образуемые взаимодействием высших гармонических тока ротора с магнитным потоком основной гармонической. Мгновенное значение такого колебательного момента
(4.91)
mкv.1 = 2cM Ф1m I2v cos[(v ± 1) ωt - ψv].
Знаки «+», «—» в скобках аргумента зависят от того, совпадает направление вращения волны МДС высшей гармонической с направлением вращения основной гармонической или нет. Например, пятая гармоническая МДС имеет отрицательное направление (см. табл. 4.2); следовательно, частота ее относительно МДС первой гармонической: n 5,1 = n 1 - (
- n 5) = n 1 - (-5n1)= 6n1. Для седьмой гармонической оба направления вращения совпадают: n7,1 = n1 - n7 = n1 - 7n1 = - 6n1. Таким образом, колебательные моменты, создаваемые парой соседних гармонических тока ротора с первой гармонической потока, имеютодну и ту же частоту (в данном случае 6n1),но противоположны по знаку.
Обычно достаточно бывает рассмотреть две пары колебательных моментов: моменты от пятой и седьмой гармонических и моменты от одиннадцатой и тринадцатой гармонических. Амплитудное значение колебательных моментов соответствующих пар (4.92)
Мкmax = Mvmax - M(v+2)max = сМ Ф1m 2(I2v - I2(v+2)). Поскольку момент от основной гармонической (4.93)
М1 = сМ Ф1m I21 cosψ21,
получаем (4.94)
Мкmax /М1 = 2 (I2v - I2(v + 2))/(I21 cosψ21).
Для крупных электрических машин согласно (4.81) (4.95)
Uv U1
Uv
Iк Uv

 Iv ≈ v√(R1 + R'2)2+ (X1 + X'2)2 ≈ √ (R1 + R'2)'+ (X1 + X'2)2 · vU1 ≈ v · U1,
Iv ≈ v√(R1 + R'2)2+ (X1 + X'2)2 ≈ √ (R1 + R'2)'+ (X1 + X'2)2 · vU1 ≈ v · U1,
где Iк - ток короткого замыкания двигателя при синусоидальном питающем напряжении. Полагая при номинальном режиме cos ψ21ном ≈ 1,0 и I 21ном ≈ Iк /k п, получаем
 Mкmax = 2 k п[1/ v 2- 1/(v + 2)2].
Mкmax = 2 k п[1/ v 2- 1/(v + 2)2].
M1ном
Значенияамплитудколебательныхмоментов,вычисленныепо формуле (4.94) при k п = 3÷5, составляют 7-12% от М 1ном для момента, изменяющегося с частотой 6ω1 (от пятой и седьмой гармонических), и 0,8—1,5% для момента, изменяющегося с частотой 12ω1 (отодиннадцатой и тринадцатой гармонических).
Амплитуда колебательных моментов не Зависит от значения нагрузки. Поэтому при небольшой нагрузке в режиме, близком к холостому ходу, амплитуда колебательных моментов может превышать основной электромагнитный момент двигателя. Это явление может вызвать неравномерность вращения ротора, особенно заметное при малых частотах, когда периоды изменения колебательного момента достаточно велики.
Билет 8
1)
Date: 2016-07-22; view: 1003; Нарушение авторских прав