Электромагнитный момент идеальной асинхронной машины

dt и,какследуетиз(1.109),момент

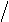сопротивления М с уравновешиваетсяэлектромагнитныммоментом М эм,которыйразвивает машина. Электромагнитный момент определяется несколькими способами.

Электромагнитный момент можно найти, если известна механическая мощность:

M эм = P 2¢ wp.

(3.75)

M эм

= P эм w,

(3.76)

. При w = 2 × p × f

p M эм

= p × P эм

Так как из (3.70) и (3.71)

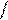
= m × (I ¢)2× r ¢

s, то

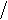M = m 1 × p × (I ¢)2 × r 2¢.

эм 1 2 2

c

(3.77)

Из (3.3), (3.4) электромагнитный момент идеальной электрической машины, в которой нет высших гармоник, определяется как произведение токов:

M = m M (is × ir - is × ir)

(3.78)

эм 2

b a a a

Заменяя произведения токов и взаимной индуктивности в (3.78)

потокосцеплениями,

M эм определяем через произведения потокосцеплений и

токов. Электромагнитный момент можно найти также через изменение энергии магнитного поля в воздушном зазоре машины:

M = dW

(3.79)

,

эм dg

где W — энергия магнитного поля в воздушном зазоре; g — угол поворота ротора

относительно статора, соответствующий электрическому углу

a = p × g

dW =

B 0 dV,

(3.80)

где

B — индукция в элементе объема dV.

зазора V

B 2

= 2 × p × R × ld × d 0

V 0

dV.

(3.81)

Рассмотренные выше выражения (3.75) — (3.81) для определения электромагнитного момента дают интегральное значение момента. При проектировании электрических машин необходимо знать распределение усилий по поверхности ротора и статора машины.

На рисунке 3.34 представлен элемент короткозамкнутого ротора асинхронной машины. Поверхностная плотность токового слоя

A = I 2× N 2×,

2 2 × p × R

(3.82)

где

I 2 = I 2 max ×

— ток в стержне обмотки ротора; N 2 — число стержней на

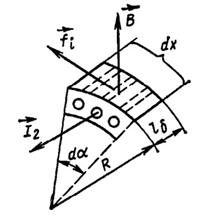
Рисунок 3.34 К определению сил, действующих на ротор

Ток в роторе и плотность токового слоя, как и индукция, распределяются по гармоническому закону (рисунок 3.35, а):

æ x ö

æ x ö

è 1

p ÷÷;

ø

A 2 = A 2 m × sinçç

p - y ÷÷.

Рисунок 3.35 Распределение электромагнитных сил по длине полюсного деления

На проводник с током, находящийся в магнитном поле с индукцией В, действует сила, Н/м,

fx = Bx × Ax × ld.

Токовый слой в поле В на всей поверхности ротора создаст момент

2 t 1

(3.83)

M эм

= R ò

f x dx,

(3.84)

где R — радиус ротора (см. рисунок 3.34). Подставляяв (3.83) значения А 2 и В и считая, что

dx = Rda, получаем

2 t 1

æ x ö

æ x ö

M эм

= R × ld

ò Bm × sinçç t

p ÷÷ × A 2 m × sinçç t

p - y ÷÷ dx =

2 t 1

è 1 ø

æ x ö

è 1 ø

æ x ö

= R 2

× ld

ò Bm

× sinçç

p ÷÷ × A 2 m

ø

× sinçç

p - y ÷÷ da =

(3.85)

Bm

A 2 m

× 2 p 2

cos(y

) = p × R 2 × l

Bm

A 2 m

cos(y

2).

Так как

Ф = 2 × B × l × t, a

m p m d 1

t = 2 p × R и

Bm =

Ф × p

m, получим среднее

× l × R

2 d

значение электромагнитного момента

× ld

× Bm × A 2 m × cos(y 2) =

Фm× p

I 2× N 2×

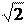cos(y) =

2 × ld × R

2 × p × R 2

(3.86)

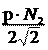
cos(y

2),

Фm и ЭДС Е 2,а также между ЭДС и МДС и током в

обмотке ротора

I 2.

Среднеезначениесилыпригармоническомраспределении В и I 2

F ср

1 2 p

2 m × ld

× sin(a) sin(a - y

2) da =

(3.87)

= 1 B × I

× l × cos(y),

2 m 2 m d 2

где

Bm,

I 2 m

— амплитудные значения индукции в воздушном зазоре и тока в

роторе.

Электромагнитные силы и электромагнитный момент по поверхности ротора распределены неравномерно и изменяют направление (рисунок 3.35, б).

В практических расчетах широко применяется выражение для расчета полученное из Г-образной схемы замещения (см. рисунок 3.20):

M эм,

U 1.

(3.88)

r 2÷

+ (x

+ C x ¢)2

1 1 2

Так как

P э2 = P эм × s = wc × M эм × s то

M = m 1 × p × (I ¢)2 × r 2¢.

c

Подставляя значение тока

I 2¢, для двухполюсной машины получаем

M = s

r 2¢ ö

÷

+ (x

ù

+ C x ¢)2 ú

(3.89)

ëè s ø

1 1 2

û

Рассматривается идеальная машина, поэтому можно, пренебрегая механическими потерями,считать,что М эм равен М — моменту на валу машины.

По (3.89) построена механическая характеристика асинхронной машины M = f (s) при U 1 и f 1=const(рисунок3.36).Механическаяхарактеристикатакжепредставляетсобой зависимость частоты вращения ротора от момента n = f (М) или наоборот М = f (n).

Рисунок 3.36 Механическая характеристика асинхронной машины M = f (s) Подставляя в (3.89) различные значения s, можно получить зависимость M = f (s) для

всех режимов работы асинхронной машины. Согласно (3.89) М =0 при s=0 и

s = ±¥

. Из (3.89) следует, что момент имеет максимум при

s = ± sk, т. е. при критическом

скольжении. При увеличении скольжения от 0 до

± sk

момент растет, а затем

уменьшается. При этом ток

I 2¢ продолжает расти, но растет реактивная

составляющая, а активная уменьшается. За счет увеличения тока

ЭДС и поток машины.

I 1 уменьшается

Считая параметры постоянными, можно определить экстремумы, приравняв

dM эм = 0.

ds

При этом критическое скольжение

s k = ±

C 1 × r 2¢.

(3.90)

r 2 + (x

+ C x ¢)2

1 1 1 2

Подставляя значение sk

в (3.89), определяем максимальный момент для

многополюсной машины:

p × m 1× U 1

. (3.91)

2 × w

× C × (± r +

r 2 + (x

+ C x ¢)2)

c 1 1 1

1 1 2

Знак «+» перед (3.91) и генераторному режимам.

r 1 относится к двигательному, а знак «—» — к

Для асинхронных двигателей единых серий и асинхронных машин большой

мощности можно считать, что

r 1 = 0 и тогда

s k = ±

C 1 × r 2¢,

x + C x ¢

(3.92)

(1 1 2)

а максимальный момент

M = ±

p × m 1 × U 1.

(3.93)

max

× w × C ×

x + C x ¢

1 2)

Максимальный момент пропорционален квадрату напряжения и обратно

пропорционален

r ¢

xk = x 1 + x 2¢. В (3.91) и (3.93) можно положить

C 1= 1 и считать,

s k = ±.

xk

При

r 1 = 0 и C 1 = 1 выражение для максимального момента имеет вид

M max

= ± p × m 1× U 1.

(3.94)

× w × x

Как следует из (3.91), максимальный момент в генераторном режиме М maxг

несколько больше, чем в двигательном М maxд. Это объясняется тем, что в

генераторном режиме

r 1 принимается со знаком «-» и знаменатель (3.91) меньше

знаменателя в (3.91) для двигательного режима. Активное сопротивление ротора

определяет

s k (3.92),и чем больше

r 2¢ тем больше s k

смещается в область больших

скольжений. Кратность максимального момента

kM = M max

M ном= 1,7 - 3,0.

Болеевысокие значения kM

полюсов.

принадлежат двигателям с меньшим числом пар

На рисунке 3.37 представлены зависимости момента от скольжения при изменении

активногосопротивленияротораи U 1 и f 1=const.Приизменении

r 2¢ максимальный

момент не изменяется, и при увеличении

r 2¢ максимум момента смещается в

область больших скольжений. Увеличить активное сопротивление обмотки ротора можно путем подключения добавочного резистора к фазной вторичной обмотке.

Рисунок 3.37 Зависимость момента от скольжения при различных активных сопротивлениях ротора

Установившееся значение пускового момента соответствует s =1. Из (3.89) пусковой момент

m × U 2 × r ¢

M п = w

× ((r

+ C r ¢)2 + (x

+ C x

)2)

(3.95)

c 1 1 2 1 1 2

r ¢. Смещая

M max

за счет увеличения

r 2¢ можно получить

M max

= M п. Это имеет место

согласно (3.93) и (3.95) при

r 2 + (x

+ C x ¢)2.

(3.96)

1 1 1 2

В большинстве электроприводов желательно иметь пусковой момент близким к максимальному. Это обеспечивает механическая характеристика с повышенным сопротивлением в цепи ротора (кривая 1 на рисунок 3.38). Однако в номинальном режиме при такой механической характеристике двигатель будет работать при большом скольжении, что связано с большими габаритами, потерями и низкими энергетическими показателями. Поэтому асинхронные двигатели с механической характеристикой 1 используются редко. Двигатели единых серий имеют механическую характеристику 2, обеспечивающую высокие энергетические показатели,когда s ном=l-4%.

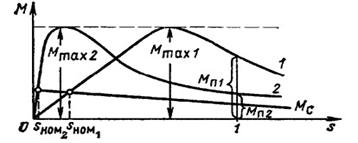
Рисунок 3.37 Механические характеристики асинхронного двигателя

Из анализа механических характеристик 1 и 2 следует, что наиболее благоприятной механической характеристикой была бы характеристика, сочетающая свойства характеристик 1 при пуске и 2 в номинальном режиме. Переход от характеристики

1 к характеристике 2 в асинхронных двигателях с фазным ротором достигается путем включения в обмотку ротора при пуске резистора и закорачивании обмотки ротора при работе в номинальном режиме. Двигатели с фазным ротором более дорогие и выпускаются для электроприводов с тяжелыми условиями пуска. В двигателях с короткозамкнутым ротором улучшенные пусковые характеристики получаются за счет применения пазов специального профиля, в которых

происходит нелинейное изменение

r 2¢ при вытеснении тока в пазах.

Выражение (3.89) для определения механической характеристики громоздкое и для упрощенных расчетов неудобное. М. Клоссом была предложена простая формула для описания механической характеристики

M = 2

M max

s + sk sk s

(3.97)

По формуле Клосса характеристика M = f (s) может быть построена с погрешностью 10—15 %, если для каких-либо двух режимов работы известны М и s. Этими двумя режимами могут быть номинальный режим и режим пуска, данные которых приводятся в каталогах.

Для устойчивой работы асинхронного двигателя и производственного механизма необходимо определенное сочетание механических характеристик двигателя М (n) и нагрузки М с(n).Двигательустойчивоработает,когда

dM < dM c

dn dn

(3.98)

Этому условию соответствует точка 1 на рисунке 3.38. После возмущения система возвращаетсяв исходное положение, так как при увеличении частоты вращения М с растет быстрее, чем момент двигателя М, и система возвращается в точку 1. При уменьшении n,наоборот, М с уменьшаетсябыстрее,чеммоментдвигателя,и система снова возвращается в точку 1.

Рисунок 3.38 К определению устойчивой работы двигателя Неустойчивый режим работы имеет место в точке 2, в которой

dM > dM c

dn dn

(3.99)

Для устойчивой работы двигателя важное значение имеет перегрузочная способность двигателя. При колебаниях напряжения сети и момента нагрузки двигатель продолжает работать, если имеется запас статической устойчивости,

определяемый коэффициентом перегрузочной способности двигателях общепромышленного применения равен 1,7—2,2.

Билет 3

Date: 2016-07-22; view: 608; Нарушение авторских прав