Условия, влияющие на форму графика распределения

{ Было бы неправильным на основании рассмотренных выше примеров сделать вывод о том, что все распределения, полученные дифференциальной психологией, соответствуют нормальному. Существует много других возможных типов частотных распределений, некоторые из них можно проиллюстрировать на примере реальных данных, полученных при исследовании некоторых качеств. Графики распределения могут отличаться от математической «нормальности», главным образом, асимметричной (скошенной набок) формой и степенью уплощенности. Асимметричное, «скошенное» распределение — это такое распределение, в котором высшая точка, или мода, смещена вправо или влево от центра. Такому распределению не хватает двусторонней симметрии, как у нормального графика. На рисунке 11 изображено скошенное распределение, при котором большинство показателей расположено в верхней части графика.

Кроме этого, отклонения от нормального распределения могут проявляться в некоторой заостренности или уплощенности верхней части графика.

На рисунке 12 изображены два графика, один из которых более заострен, а другой — более уплощен, чем теоретический нормальный график. В первом из них

Рис. 12. Распределение (А) заостренного типа и (В) уплощенного

46 Дифференциальная психология

(график А) наблюдается чрезмерный рост количества случаев в центре с одновременным уменьшением их количества у крайних значений шкалы. Во втором (график В) случаи распределены более равномерно на протяжении длинного отрезка. Мультимод-ный график можно рассматривать как другой вариант заостренного распределения. Как видно из названия, этот тип графика имеет не одну моду, или не один пик. Таким образом, показатели индивидов будут концентрироваться в двух и более различных точках шкалы. Пики могут быть в равной степени высокими или один пик может быть выше другого.

Графики распределений, существенно отличающиеся от нормальных и проявляющих одну или несколько характеристик, описанных выше, появляются время от времени при наличии некоторых условий. Знание этих условий необходимо для правильной интерпретации частотных распределений. Главными факторами, которые могут оказать влияние на форму графика распределения, являются: неадекватность выборки, использование неудачных или непригодных средств измерения и некоторые факторы, воздействующие непосредственно на исследуемое качество. Сейчас мы рассмотрим по порядку каждое из этих условий.

Выборка. Чтобы получить любой заданный тип распределения, достаточно просто специально подобрать испытуемых, соответствующих этому типу. Естественно, такая процедура не будет объективной. Подобная изменчивость может быть результатом действия факторов отбора, на которые исследователь не всегда обращает внимание. Каждый раз, когда график распределения существенно отличается от нормального, встает вопрос об адекватности выборки.

Например, скошенность может быть результатом включения в состав единого распределения двух нормально распределенных групп, имеющих выраженные отличия друг от друга по значению. Иллюстрацией такого эффекта может быть рисунок 13. В варианте А даны отдельные графики распределения по двум группам, у одной из которых более низкое среднеарифметическое значение и меньше разброс результатов, чем у другой. В варианте В график имеет скошенный вид, который получился в результате объединения графиков распределения двух групп в общий график распределения.

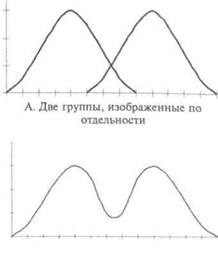
В. Две соединенные группы

Рис. 13. Асимметрия, причиной которой является объединение групп с разными значениями

Б. Две соединенные группы

Рис. 14. Бимодальная результирующая, полученная от объединения

двух групп, имеющих сильно различающиеся области значений.

Мультимодный график также получается тогда, когда тестируемая выборка не является случайной по отношению к общей популяции, но состоит из индивидов, отобранных с разных уровней и объединенных в единую группу. Например, группа, состоящая из 5- и 10-летних детей, будет непременно давать бимодальное распределение как по показателям теста на умственные способности, так и по результатам измерения роста, веса и многих других характеристик. Если бы в эту выборку были включены группы детей от 6 до 9 лет, то распределение имело бы вид нормального, колоколообразной формы графика.

Как получаются бимодальные распределения в результате подобного объединения двух сильно различающихся групп, видно на рисунке 14. Легко заметить, что у них мало общих точек. Когда их много, как в случае с близкими возрастными группами, результирующий объединенный график будет нормальным и с одной вершиной.

Другие особенности могут зависеть от того, заключен ли сам по себе в выборке уплощенный график распределения, или,

48 Дифференциальная психология

наоборот, имеющий форму пика. Последнее случается, например, тогда, когда выборка носит исключительно гомогенный характер. В заключение отметим, что неограниченное количество незначительных отклонений и изменений в графиках распределения может быть следствием тестирования малых групп. Графики, начерченные на основании обработки малого количества случаев, обычно представляют собой неровные, зубчатые линии — так проявляется разброс индивидуальных значений. В принципе, чем больше выборка, тем «более гладким» будет график распределения.

Средства измерения. Некоторые особенности тестов или других средств измерения, применяющихся для сбора данных, могут также влиять на форму результирующего графика распределения. Так, если уровень сложности вопросов теста искусственно завышен или занижен, то это может сделать форму графика скошенной. Такое происходит, когда какой-нибудь тест предлагают пройти группе, для которой он не предназначен. Например, если тест на умственные способности, составленный для учеников 3 — 8 классов, предложить учащимся колледжа, подавляющее большинство испытуемых покажут результаты, близкие к максимальным; низких же показателей не будет вообще. Точно так же, если один из многочисленных тестов, разработанных для первокурсников колледжа, дать учащимся начальной школы, это вызовет резкое увеличение количества значений, близких к нулю, и распределение будет также асимметричным.

Очевидно, что на основании таких данных нельзя делать вывод об аномальном распределении умственных способностей среди детей или студентов колледжа. Скошенное распределение, полученное в этих случаях, будет свидетельствовать о том, что уровень сложности теста не включает в себя в равной мере более сложные и более простые задания. В одном случае все испытуемые покажут очень высокие значения, в то время как, если бы тест включал в себя вопросы посложнее, результаты испытуемых распределились бы по всей шкале и более равномерно. Иллюстрацией к этому может служить рисунок 15, на котором сплошная линия показывает реальное распределение способностей в группе, а пунктирная линия — результат использования теста с низким уровнем сложности. Подобным образом, боль-

Рис. 15. Скошенное распределение, полученное в результате использования теста с низким уровнем сложности

шое количество нулевых значений или значений, близких к нулю, мы получим, если тест окажется для группы слишком сложным. Подбирая для данной группы тест, надо удостовериться, что испытуемые способны показывать результаты, которые будут отражены на обоих концах шкалы. Их показатели должны существенно отличаться как от нуля, так соответственно и от сверхвысоких значений.

I

18,000

16,000

14,000

12,000

10,000

8,000

6,000

4,000

2,000

о см

о го

о

о

Л

о со

о

Показатели теста

со

* Последний интервал не покрывает 10 пунктов, поэтому максимальным показателем теста является 76.

Рис. 16. Распределение показателей 70805 11-летних шотландских детей по

данным вербального группового теста на умственные способности. (Данные

Шотландского совета по исследованиям в образовании, 25, с. 82.)

50 Дифференциальная психология

Реальным примером того, какой эффект на низких значениях шкалы возникает при использовании теста с неадекватным уровнем сложности, является рисунок 16. Данные, отраженные в этом распределении, были собраны в 1947 году в ходе проведения одного исследования в Шотландии, целью которого было протестировать каждого 11-летнего ребенка, родившегося в Шотландии. Данное исследование представляет собой одно из самых широких из когда-либо предпринимавшихся. В нем приняли участие 70805 детей, составивших выборку, которую авторы объявили «полной»; в нее не вошли только те дети, чьи сенсорные или моторные возможности не позволяли им пройти тест наравне с другими, дети, отсутствовавшие в школе в тот день, когда проводилось тестирование, и дети, посещавшие некоторые частные школы. Согласно подсчетам, в тестировании приняли участие 88 % всех 11-летних детей, живших в Шотландии в то время. Всем испытуемым давали специально разработанный 45-минутный групповой тест на умственные способности, который включал в себя две страницы с рисунками и пять страниц с вербальными заданиями.

Распределение показателей по вербальному тесту дано на рисунке 16. И хотя в целом это распределение показывает скопление результатов в центре и их активное снижение в точках крайних значений, в нем можно заметить ряд несоответствий. Это касается, прежде всего, того конца шкалы, на котором расположены низкие значения. Фактически 13,9 % случаев, падающих на интервал 0—9, показывают, что нулевое значение теста, возможно, оказалось слишком завышенным для данной популяции. Если бы в тест были включены более легкие вопросы, то весьма вероятно, что значения распределились бы еще по нескольким интервалам, которые оказались бы ниже нулевого уровня данного теста.

Искажать частотное распределение может также неравенство единиц измерения. Хорошей иллюстрацией этого могут послужить данные по остроте зрения, собранные в результате использования двух разных тестов (28). Частотное распределение одной и той же группы из 226 человек по каждому их этих тестов показано соответственно в частях А и В на рисунке 17.

График А представляет собой несколько скошенный острый пик, полученный при тестировании с использованием таб-

Рис. 17. Влияние неравенства единиц измерения разных шкал на графики

распределения: распределение 226 человек по результатам двух тестов на

остроту зрения. (Данные из Тиффин и Уирт, 28, с. 77.)

лицы Снеллена, — индекс остроты зрения здесь зависит от распознания ряда самых мелких букв со стандартной дистанции в 20 футов. Так, индивид, который с 20 футов способен разглядеть только те буквы, которые средний человек различает с расстояния 50 футов, имеет индекс ²⁰/₅₀. Нормальное зрение, очевидно, соответствует индексу ²⁰/₂₀. Индекс ²⁰/₁₅ означает, что зрение по остроте превосходит средний уровень. Из-за особого подбора размеров букв в этом тесте не все уровни остроты зрения можно свести к единому знаменателю, вследствие чего на более низких уровнях остроты зрения можно получить индекс больше реального, в отличие от среднего или высшего уровней остроты зрения. Иными словами, различия в уровне сложности между следующими друг за другом рядами букв не равноценны; «скачков» в уровне сложности больше в центре и на отрезке более высоких значений шкалы остроты зрения, чем на отрезке более низких значений.

Неравенство единиц измерения можно проиллюстрировать, сравнив единицы измерения таблицы Снеллена с соответствующей шкалой равных единиц для измерения остроты зрения (28, с. 77):

52 Дифференциальная психология

Шкала

равных единиц 12 3 4 5 6 7 8 9 10 11 12 13 14 15

ТяКпипя Снеллена 2Q2Q202022 20_20_ 20 Ж 20

Таблица Снеллена ₂00 100 70 50 40 30 25 20 15 13

Распределение показателей той же группы из 226 человек по шкале остроты зрения с равными единицами измерения представлено в части В рисунка 17. Видно, что этот график больше напоминает график нормального распределения, чем график распределения значений с неравными единицами измерений.

Другие случаи отклонений от нормального распределения могут так же иметь причиной неравенство значений шкалы. Предположим, что в приведенном выше примере полностью задействованы значения обоих концов шкалы, а на отрезке среднего уровня сложности наблюдается недостаток. В результате может получиться распределение с двумя пиками, поскольку индивиды, чьи значения реально располагались бы в центре, займут ближайшие доступные уровни. Об этом эффекте полезно вспомнить при рассмотрении результатов, полученных при тестировании некоторых личностных характеристик, таких, например, как интроверсия—экстраверсия. Такие качества, для обозначения которых используются биполярные термины, могут быть наиболее полно представлены в своих крайних характеристиках, в то время как их средние значения могут быть задействованы сЗгабо. В таком тесте в центре шкалы ее деления располагались бы реже, чем на отрезках ее крайних значений. В результате весьма вероятным было бы возникновение небольшой бимодности, которая являлась бы следствием особенностей средства измерения, но не свойств испытуемых. Подобным образом, при увеличении числа пунктов на крайних отрезках шкалы, нормальное распределение может быть преобразовано в относительно плоское.

Теперь мы видим, что измерительная шкала может воздействовать на форму графика распределения по-разному. Строго говоря, невозможно определить истинное распределение, если у нас нет шкалы с равными единицами измерения. Но мы в настоящее время можем разрабатывать такие шкалы с равными единицами для психологических тестов, только если предположим, что тестируемое качество относится к нормально распределенным! При этом спрашивать, что это за «истинное» распре-

Распределение индивидуальных различий 53

деление психологического качества бессмысленно по крайней мере сейчас.

В процессе создания теста нормальный график рассматривается скорее как методологическая проблема, чем как эмпирически наблюдаемый факт. Всякий раз, когда стандартизированная группа показывает распределение, которое нельзя признать нормальным, обычной реакцией должно быть изменение теста. Большинство тестов, таким образом, видоизменялись до тех пор, пока они не давали в популяции, для которой предназначались, распределения, приближенного к нормальному. Некоторые пункты шкалы удалялись или добавлялись, другие перемещались по шкале вверх или вниз; при этом исследователь каждый раз оценивал, к чему приводят подобные изменения, и, в конце концов, добивался желаемой приближенности распределения к нормальному виду. Поэтому, говоря, что данное распределение нормальное, мы подразумеваем, что был проведен процесс дотошной стандартизации данного теста. И наоборот, говоря, что данное распределение не соответствует норме, мы подразумеваем только то, что тест получился неудачным или что тест применялся к группе, для которой он был не пригоден.

Есть несколько причин, по которым разработчики тестов и исследователи в области дифференциальной психологии обычно стремятся получить нормальное распределение. Если делать допущения относительно распределения какого-либо человеческого качества, нормальный график в большинстве ситуаций является наиболее вероятным. Известная сложность и множественность факторов, определяющих то, как данное качество проявляется у индивида, заставляет нас ожидать, что оно будет распределяться в соответствии с теорией вероятности. Более того, распределение физических качеств, измеряемых равными единицами измерения, такими как дюймы или фунты, дает графики нормального распределения. Другой причиной стремления к поиску соответствия с нормальным распределением является та, что нормально распределенные данные позволяют подвергать их различным типам статистического анализа, который в противном случае оказывается неприменимым. Однако следует иметь в виду, что другие типы распределения могут быть предпочтительны для некоторых специальных целей и соответствующим образом использоваться.

54 Дифференциальная психология

Специальные факторы. Отклонения от нормального графика могут быть в большей степени результатом воздействия определенных условий на сами исследуемые характеристики, чем следствием непродуманной выборки или применения негодных средств. Примером может служить так называемая гипотеза J-кривой социальной конформности, впервые предложенная Оллпор-том (1). Эта кривая, названная из-за своего сходства с буквой J, может рассматриваться как сильно скошенный график, в котором при распределении большинство показателей приходится на один его конец, представляющий собой полную или почти полную конформность к социально принятому стандарту поведения. Лучшей иллюстрацией такой J-кривой являются графики реакции автомобилистов или пешеходов на регулирование дорожного движения: на остановку транспортных потоков, пересечение перекрестков или движение по транспортной полосе. Другие примеры «конформистского поведения», к которому была бы применима J-кривая, включают определенные религиозные обычаи, такие как время прихода на службу, участие в групповом пении и т. п.

Типичные J-кривые изображены на рисунках 18 и 19.

На рисунке 18 показано распределение реакций 102 автомобилистов на перекрестке без поперечно идущего транспорта, но с красным сигналом светофора и регулировщиком. Надо отметить, что в 90 % наблюдавшихся случаев автомобилисты полностью останавливались. В пределах оставшихся 10 % некоторые существенно снижали скорость, некоторые ехали чуть медленнее и очень мало было тех, кто продолжал ехать с той же скоростью. Можно было бы предположить, что если бы все зависело

А — остановка; В — очень медленно; С — чуть медленнее; D — с той же скоростью

Рис. 18. J-кривая поведения автомобилистов на перекрестке при отсутствии поперечно идущего транспорта, но с красным сигналом светофора и регулировщиком. (Данные из Оллпорта, 1, с. 144.)

Распределение индивидуальных различии 55

только от их собственного выбора, автомобилисты могли бы продемонстрировать поведение, которое более или менее совпало бы с нормальным распределением. Но введение таких факторов «социального давления», как регулирование транспорта с помощью светофора и полисмена, повлияло на изменение распределения, придав ему вид J-кривой.

Необходимо отметить, что местоположение пика зависит от того пункта на шкале, на который падает социально обусловленное поведение. Крайние значения реальной J-кривой проявляются не во всех ситуациях социального конформизма. Так степень, до которой напиваются городские взрослые американцы, возможно, предстанет на графике в виде пика, но это не будет действительно крайняя точка, а всего лишь средняя, соответствующая «умеренному социальному уровню». Эта точка, возможно, проявляет максимальный конформизм для групповой практики, но она не отражает ни максимума, ни минимума в питейном поведении. Важна не сама по себе J-кривая, но, скорее, тот факт, что изменения в графике распределения могут быть инспирированы социальным конформизмом. J-кривая — это всего лишь конкретный пример, вызванный этим фактором. Мимоходом добавим, что кривая на рисунке 18 на самом деле представляет собой обращенную в другую сторону J, которую точнее можно назвать L-кривой. Но по договоренности все подобные очень сильно скошенные кривые принято называть J-кривыми, безотносительно к тому, является ли пик левым или правым крайним значением. Конечно, положение шкалы может быть произвольно изменено так, чтобы пик находился слева или справа.

Несколько иное применение понятия J-кривой дается в недавно проведенном исследовании юношеского поведения в отношении ровесников (20). В этом исследовании 629 студентам-первокурсникам дали списки с именами их одногруппников (в группе в среднем 35,5 человек) и попросили проставить напротив имен номера от 1 до 5, соответствующие следующим утверждениям: «Хотелось бы, чтобы он был моим лучшим другом», «Хороший друг», «Не дружеские, но нормальные отношения», «Не знаком с ним» и «Чужой человек в группе». Для построения таблицы исследователь соединил первые два рейтинга в категорию «принятие», последние два — в категорию «изоляция и не-

Рис. 19. J-кривая, показывающая принятие сверстников юношами и девушками. (Данные из Пепински, 20, с. 536.)

приятие», а центральный — выделил в качестве категории «пассивного принятия, или терпимости». Результаты распределения изображены на рисунке 19. Два графика в части А показывают рейтинги, данные юношами другим юношам и девушкам в своих группах. Соответствующие графики рейтингов, данные девушками, показаны в части В. Согласно мнению исследователя, эти графики показывают конформизм, присущий в нашей культуре большинству юношей и девушек в возрасте полового созревания или немного моложе. Как следствие, они отражают широкое принятие испытуемыми тех, кто относится к одному с ними полу и возрасту в сочетании с тенденцией избегать представителей противоположного пола — эта тенденция сильнее в юношах, чем в девушках.

Здесь необходимо предостеречь: мы не должны делать вывод о причинах проблемного поведения на основании формы графика. Как отмечалось в предыдущих разделах, на форму графика могут влиять свойства шкалы измерения. Например, выделив центр шкалы, мы можем из нормально распределенной переменной получить J-кривую. Подобно любому другому частот-

Распределение индивидуальных различий 57

ному распределению J-кривую можно исследовать с точки зрения адекватности измерительной шкалы, процедур выборки и других условий, которые могут повлиять на форму распределения.

Другим фактором, который может давать частотное распределение в форме J-кривой, является разреженность рассматриваемого феномена. Когда всеобщая частота события в изучаемой выборке является низкой, его ожидаемое вероятностное распределение имеет скошенную форму, известную статистикам как распределение Пуссона. Чем реже проявляется феномен, тем более скошенным будет график этого распределения. Одной из лучших иллюстраций этого типа распределения в психологии является частота аварий (3, 18). Например, если у 200 человек за определенный период времени произошло 100 аварий, ожидаемое вероятностное распределение будет следующим: у 121 человека не должно произойти аварий; у 61 должна произойти 1; у 15 должно произойти 2; и у 3 должно произойти по 3 аварии (ср. 3, ее. 456—457).

Этот тип распределения представлен на рисунке 20 графиком А, который показывает действительное число аварий, происшедших у 59 водителей в течение одного месяца. Можно сказать, что здесь мы имеем дело с J-кривой, пик которой совпада-

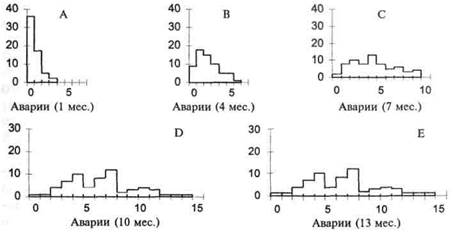
Рис. 20. Распределение аварий у 59 водителей за разные периоды времени.

(Данные из Personnel and Industrial Psychology by E. E. Ghiselly and C. W. Brown,

1955, McGraw-Hill Company, Inc., p. 343.)

58 Дифференциальная психология

ет с полным конформизмом, предполагающим соблюдение правил безопасности, и с отсутствием аварий. Или мы можем попытаться объяснить форму распределения по-другому, например присутствием малой группы «склонных к аварии» людей. Взглянув на другие графики на рисунке 20, можно сказать, что главный фактор в действительности оказывается артефактом конкретной наблюдаемой выборки.

Если продлить время нашего наблюдения за 59 водителями до 13-месячного периода, мы получим распределение, показанное на графике 20Е. Хотя на нем представлено несколько незначительных отклонений, данное распределение, естественно, не является J-кривой, его пик приходится приблизительно на центр ряда значений. С удлинением периода наблюдения общее число аварий в нашей выборке из 59 человек увеличивается, и, следовательно, распределение становится все менее скошенным. Последней иллюстрацией специальных факторов, которые могут повлиять на форму графика распределения, являются патологические условия. Например, есть основания полагать, что распределение IQ в полной популяции показывает преобладание очень низкого IQ по сравнению с теми значениями, которые ожидались при нормальном распределении (ср. 23). В одном тщательно проведенном исследовании почти полной популяции детей, родившихся в течение четырех лет в английском городе Басе, доля случаев с IQ ниже 45 оказалась примерно в 18 раз больше, чем ожидалась с точки зрения нормального распределения (23).

Наиболее достоверным объяснением такого отклонения от нормы является ссылка на вторичные факторы, такие как заболевания, ненормальные условия жизни или большее число, по сравнению с ожидаемым, доли слабоумных детей (ср., например, 22). Напомним, что нормальное распределение получается тогда, когда измерение некоей переменной представляет собой совокупный результат очень большого числа измерений независимых и в равной степени значимых факторов. Рассматривая чрезвычайно большое число как наследственных факторов, так и факторов среды, влияющих на развитие умственных способностей в общей популяции, разумно ожидать распределения IQ в соответствии с нормальным графиком. Некоторые формы умственной отсталости, такие как дебильность, появляются, скорее в результате действия какого-либо единичного фактора, чем

Распределение индивидуальных различий 59

множественных факторов. Иными словами, некоторые патологические условия, развивающиеся под воздействием наследственности и среды, при прочих равных обстоятельствах могут быть непосредственной причиной возрастания числа случаев умственной отсталости. Поэтому на отрезке низких значений графика распределения эти единичные факторы суммируются с множественными факторами, вероятными при нормальном распределении.

Попутно дополним, что имеющиеся данные по отрезку низких значений графика распределения интеллектуального уровня, так же как и интерпретация этих данных, носят пока в основном предварительный характер. Мы привели их здесь лишь для того, чтобы проиллюстрировать возможные следствия действия патологических условий, «наложенных» на форму графика распределения.

Подытожим сказанное: если мы исходим из ожидания, что графики распределений будут в целом похожи на нормальный график, любое отклонение от нормы становится проблемой для исследования. Такой подход к форме распределения весьма плодотворен для раскрытия механизма действия различных факторов. Например, существенное отклонение от нормы может означать, что высшие значения теста занижены, а его нулевая отметка завышена или что вопросы теста не соответствуют отрезку определенной сложности. Кроме этого, могут стать очевидными некоторые факторы, которые до недавнего времени скрыто воздействовали на изучаемую выборку. И наконец, форма полученного распределения может послужить ключом к раскрытию того существенного влияния, которое вместе с изменением графика распределения изменяет само качество. Иными словами, любое существенное отклонение от нормы должно настораживать исследователя и побуждать его к дальнейшим исследованиям.

Date: 2016-07-22; view: 342; Нарушение авторских прав