Замена переменной, формула интегрирования по частям в определенном интеграле.

Пусть функция 𝑓 (𝑥) непрерывна на отрезке [a; 𝑏], а функция 𝑥 = 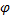(𝑡) имеет непрерывную производную на отрезке [𝛼; 𝛽], причем отрезок [a; 𝑏] является множеством значений функции 𝑥 = 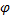(𝑡) и 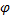(𝛼) = a, 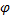(𝛽) = 𝑏. Тогда справедлива формула 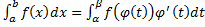называется формулой замены переменной в определенном интеграле.

Пусть 𝐹—первообразная для функции 𝑓, т.е. 𝐹 ′(𝑥) = 𝑓 (𝑥), 𝑥 ∈ [a; 𝑏]. Тогда имеем: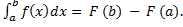

Положим 𝐺(𝑡) = 𝐹 (𝜙(𝑡)). По правилу дифференцирования сложной функции получим, что

𝐺′(𝑡) = 𝐹 ′(𝜙(𝑡))𝜙′(𝑡) = 𝑓 (𝜙(𝑡))𝜙′(𝑡).

Следовательно, функция 𝐺(𝑡) есть первообразная для функции 𝑓 (𝜙(𝑡))𝜙′(𝑡) на отрезке [a; 𝑏], и по формуле Ньютона—Лейбница найдем: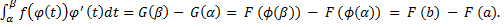

Пример: Найти интеграл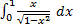

Решение. Воспользуемся формулой замены переменной. Положим 1 − 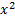= 𝑡, −2𝑥 𝑑𝑥 = 𝑑𝑡. Очевидно, 1 − 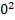= 1, 1 − 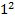= 0. Получим:

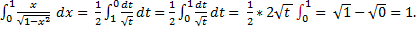
Если функции u = u(x) и v = v (x) имеют непрерывные производные на отрезке [a; b], то

справедлива формула: называют формулой интегрирования по частям в определенном интеграле.

Пример: Найти интеграл

Решение. Воспользуемся формулой интегрирования по частям:

Date: 2016-07-22; view: 283; Нарушение авторских прав