Ускорение буксира при свободном движении

;

Ускорение танкера при свободном движении

Если , то это совместное движение. Если же то буксир отстанет от танкера. Следовательно, условие потери контакта имеет вид:

Условие потери правого контакта при вращательном движении ротора

двигателя и объекта имеет вид:

.

Условие потери левого контакта:

.

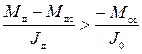При расчете переходных процессов в электроприводе с люфтом нужно при наличии контакта проверять на каждом шаге условие потери контакта. При отсутствии контакта надо проверять, не произошел ли контакт и какие скорости вращения будут после удара.

Электропривод с упругими связями. Уравнения

Упругость – свойство тел изменять размеры и форму под действием усилий и моментов, а после их снятия восстанавливать размеры и форму.

Рассмотрим упругий стержень, к концам которого приложены моменты М ₁, М ₂ (см. рис. 15.1). Концы имеют углы поворота α₁ и α₂, коэффициент жесткости стержня с ₁₂ . Если не учитывать момент инерции стержня, то из условия равновесия моментов получаем равенства

М ₂ + М ₁ = 0; М ₂= – М ₁ ;

М ₁ = с ₁₂(α₁ – α₂); М ₂ = с ₁₂(α₂ – α₁).

Рис. 15.1. Упругий стержень под действием двух моментов

Теперь рассмотрим трехмассовую систему, состоящую из ротора электродвигателя и двух цилиндров, установленных на валы в опорах (см. рис.15.2). Валы двигателя и двух цилиндров связаны упругими стержнями с коэффициентами жесткости с ₁₂ и с ₂₃ .

Рис. 15.2. Трехмассовая система с упругими связями

Первое тело (ротор двигателя) имеет момент инерции J ₁, угол поворота α₁ и частоту вращения ω₁. Имеется электромагнитный момент М ₁ и статический момент сопротивления М _1с . Второе тело имеетмомент инерции J ₂, угол поворота α₂, частоту вращения ω₂ и статический момент сопротивления М _2с.Третье тело имеетмомент инерции J ₃, угол поворота α₃ , частоту вращения ω₃ и статический момент сопротивления М _3с .

Тело с двумя закрепленными точками или на валу в опорах имеет одну степень свободы. Его движение описывается уравнением динамики и уравнением кинематики:

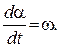
Здесь М_Σ – суммарный момент, приложенный к телу.

Наша система имеет три степени свободы и описывается шестью уравнениями:

;

;

;

;

;

.

Следует обратить внимание, что угол поворота каждого тела входит в свое уравнение со знаком ''–'', а в уравнения других тел – со знаком ''+''.

Колебания двухмассовой системы с упругой связью

Рассмотрим два цилиндра, насаженные на валы, установленные в опоры. Между валами имеется упругий стержень с коэффициентом жесткости с. Первое тело имеет момент инерции J ₁, угол поворота α₁ и частоту вращения ω₁. Второе тело имеетмомент инерции J ₂, угол поворота α₂ и частоту вращения ω₂ (см. рис. 15.3). Моменты сопротивления не учитываются.

Рис. 15.3. Двухмассовая система с упругой связью

Двухмассовая система описывается двумя уравнениями динамики и двумя уравнениями кинематики:

С учетом уравнений кинематики можно записать два уравнения второго порядка относительно углов поворота тел:

(15.1) (15.2)

Разделим левые и правые части уравнений (15.1), (15.2) на моменты инерции J ₁, J ₂соответственно и вычтем из первого уравнения второе:

(15.3)

Обозначим угловую деформацию стержня (угол закрутки)

.

Уравнение (15.3) принимает вид

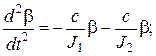
(15.4)

Обозначив

получаем дифференциальное уравнение

(15.5)

Характеристическое уравнение

имеет чисто мнимые корни

Им соответствует общее решение

Записав уравнения (15.1), (15.2) в виде

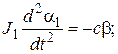
получаем выражения для углов α₁, α₂:

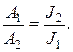
Графики углов α₁, α₂ показаны на рис. 15.4. Видно, что их колебания находятся в противофазе. Момент инерции J ₁ < J ₂, и амплитуда колебаний угла α₁ больше амплитуды колебаний угла α₂. При учете моментов трения и аэродинамических моментов колебания будут постепенно затухать.

Рис. 15.4. Графики углов при свободных колебаниях двухмассовой системы

Электромагнитный переходный процесс при включении двигателя постоянного тока независимого возбуждения

Электромагнитный переходной процесс.

Электромагнитный переходной процесс наблюдается, когда скорость вращения якоря постоянна или равна нулю, а индуктивность якоря L _я при этом

учитывается. Переходный процесс связан с магнитной инерционностью.

Предположим, что ω = 0, тогда справедливо уравнение

. (17.5)

Левую и правую части уравнения (17.5) поменяем местами и разделим на r _я . Тогда получим:

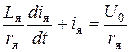. (17.6)

Обозначим

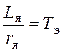(Т _э – электромагнитная постоянная времени);

Уравнение (17.6) принимает вид

. (17.7)

Будем искать решение уравнения (17.7) в виде

,

где принужденная составляющая i _п является решением того же уравнения в установившемся режиме. Если i _п = const, то . Возьмем i _п = i _∞.

Свободная составляющая i _с является решением однородного уравнения

. (17.8)

Напишем характеристическое уравнение

,

решение которого имеет вид

.

Тогда

, .

Возьмем i _я (0) = 0, тогда

i _∞ + A = 0,

откуда следует

A = –i _∞;

График тока якоря приведен на рис. 17.3.

Рис. 17.3. Зависимость тока якоря от времени

при электромагнитном переходном процессе

За время переходного процесса можно принять величину 3 Т _э

Электромеханический переходный процесс при включении двигателя постоянного тока независимого возбуждения

Допустим, что напряжение возбуждения двигателя постоянного тока и магнитный поток постоянны, а индуктивность обмотки якоря мала:

u _в = const; Ф = const; L _я = 0.

Тогда мы получим уравнения:

, (17.1)

. (17.2)

Электромеханический переходный процесс наблюдается, когда индуктивность якоря L _я = 0 и магнитный поток считается постоянным. Выразим из уравнения (17.2) ток i _я:

.

Подставим полученное выражение для тока i _я в уравнение (17.1):

;

;

Предположим, что u _я = U ₀ = const. Разделим левую и правую части на с Ф:

.

Обозначим

= Т_{э м}; (Т _эм – электромеханическая постоянная времени);

; (ω₀ – скорость холостого хода);

Уравнение примет вид

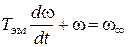, (17.3)

где .

Решение уравнения будем искать в виде суммы

.

Принужденная составляющая ω_п является решением того же уравнения в установившемся режиме. Его ищем по виду правой части. Если ω_п = const, то

.

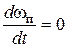Возьмем .

Свободная составляющая ω_с является решением однородного уравнения:

. (17.4)

Напишем характеристическое уравнение:

,

решением которого является

.

Если , то .

Рис. 17.1. Семейство решений дифференциального уравнения (17.3)

Общее решение уравнения (17.3) будет иметь вид:

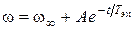
Предположим, что , тогда

, откуда ,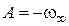

.

На рис. 17.1 показано семейство решений дифференциального уравнения (17.3) тонкими линиями. Решение при нулевом начальном условии показано жирной линией.

Рис. 17.2. Свойства экспоненты

На рис. 17.2 показана экспонента. Через время Т _эм экспонента уменьшается в е = 2,71828 раз. За время 2 Т _эм она уменьшится в е ² раз. Через время 3 Т _эм экспонента уменьшается приближенно в 20 раз, тогда считают, что переходной процесс заканчивается (остается 5 % от первоначального значения экспоненты).

Если в начале координат провести касательную к экспоненте, то она пересечет предельное значение ω_∞ в момент времени Т _эм. Если провести касательную к экспоненте в момент Т _эм, то она пересечет предельное значение ω_∞ в момент времени 2 Т _эм, и т.д.

Переходный процесс при включении обмотки возбуждения двигателя постоянного тока

Рассмотрим переходный процесс при включения обмотки возбуждения двигателя постоянного тока на постоянное напряжение. Уравнение баланса напряжений имеет вид:

или

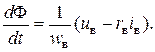
Тогда при переходе от времени t ко времени t + Δ t согласно методу Эйлера магнитный поток получит приращение

Видно, что это приращение пропорционально разности между установившимся и текущим значениями тока возбуждения.

Сущность метода поясняет рис. 19.1.

Рис. 19.1. Построение переходного процесса при включении обмотки возбуждения

Слева расположена кривая намагничивания Ф = f (i _в). При нулевом токе возбуждения имеется остаточный поток Ф _r. Вертикальная штриховая линия проведена на уровне установившегося тока возбуждения i _в∞. Справа расположена система координат (t, Ф). На оси времени t отложены отрезки Δ t, 2Δ t, 3Δ t, Влево от начала координат отложен отрезок длиной h.

Кривая Ф(t) начинается из точки (0, Ф _r). Отложим отрезок длиной i _в∞ от начала координат вверх и полученную точку b соединим с левой точкой a отрезка h. Затем через начало координат проведем отрезок, параллельный отрезку ab, до перпендикуляра, восстановленного из точки Δ t. Получим значение Ф(Δ t). Отложим это значение на левом графике и найдем значение тока возбуждения i _в(Δ t). Далее отложим отрезок длиной i _в∞ – i _в(Δ t) от начала координат вверх и полученную точку с соединим с левой точкой a отрезка h. Затем через точку Δ t, Ф(Δ t) проведем отрезок, параллельный отрезку aс, до перпендикуляра, восстановленного из точки 2Δ t. Получим значение Ф(2Δ t), и т.д.

Видно, что значение магнитного потока Ф стремится к установившемуся значению Ф_∞, а значение тока – к установившемуся значению i _в∞. Далее, полученные кривые существенно отличаются от экспонент. Особенно это касается кривой тока, которая имеет S-образную форму. Для сравнения штриховой линией проведена экспонента, стремящаяся к тому же значению i _в∞. Можно сделать общий вывод, что с увеличением тока возбуждения и магнитного потока электромагнитная постоянная времени уменьшается.

Электромеханический переходный процесс при включении двигателя постоянного тока последовательного возбуждения

Уравнение механики для двигателя постоянного тока последовательного возбуждения имеет вид

Согласно методу Эйлера запишем выражение для приращения скорости вращения:

Видно, что это приращение пропорционально разности между электромагнитным моментом и статическим моментом нагрузки.

Геометрическая интерпретация метода дается на рис. 19.2. Слева расположена механическая характеристика двигателя постоянного тока последовательного возбуждения ω = f (M) и механическая характеристика исполнительного механизма ω = f (M _с). Точка их пересечения дает значение установившейся

Рис. 19.2. Построение переходного процесса при пуске двигателя

постоянного тока последовательного возбуждения

скорости вращения ω_∞.Справа построены оси координат t и ω. На оси времени t отложено несколько одинаковых отрезков длиной Δ t. Влево от оси t отложен отрезок длиной h.

Начальное значение скорости вращения ω равно нулю. Измеряем расстояние между точками M _c и M на оси M, т.е. при ω = 0, и откладываем этот отрезок на оси ω на правой части рис. 19.2. Затем проводим отрезок, соединяющий верхнюю точку b отложенного отрезка с левой точкой a отрезка h. Теперь проводим через начало координат отрезок, параллельный отрезку ab, до пересечения с перпендикуляром, восстановленным из точки Δ t.

Получим значение ω(Δ t). Отложим это значение на левом графике и найдем соответствующие значения моментов M и M _c. Далее отложим отрезок длиной M – M _c от начала правой системы координат вверх и полученную точку c соединим с левой точкой a отрезка h. Затем через точку Δ t, ω(Δ t) проведем отрезок, параллельный отрезку aс, до перпендикуляра, восстановленного из точки 2Δ t. Получим значение ω(2Δ t), и т.д.

Видно, что значение скорости вращения ω стремится к установившемуся значению ω_∞. Далее, полученная кривая существенно отличается от экспоненты. Для сравнения штриховой линией проведена экспонента, стремящаяся к тому же значению ω_∞. Можно сделать общий вывод, что с увеличением скорости вращения электромеханическая постоянная времени растет.

Отметим, что электромагнитные процессы в двигателе здесь не учитываются, т.е. полагается, что момент инерции исполнительного механизма велик, и электромеханическая постоянная времени значительно больше электромагнитной постоянной времени.

Установившийся и переходный процессы. Решение неоднородного дифференциального уравнения

Установившимся называется процесс, протекающий долго, не меняя своего характера. Переходным называется процесс между двумя установившимися режимами.

Рис. 16.1. Примеры установившихся процессов для тока

На рис. 16.1 приведены примеры установившихся процессов для электрического тока – постоянный ток, переменный (синусоидальный) ток и несинусоидальный периодический ток. Для электропривода под установившимся обычно понимается процесс вращения с постоянной скоростью либо периодические угловые колебания исполнительного механизма..

Переходные процессы связаны с механической, магнитной, электрической и тепловой инерцией. Кинетическая энергия движущегося линейно тела с массой m определяется выражением

При ограниченной мощности источника силы энергия является непрерывной функцией времени, откуда следует непрерывность скорости движения v.

Кинетическая энергия вращающегося в подшипниках тела с осевым моментом инерции J определяется выражением

При ограниченной мощности источника момента энергия является непрерывной функцией времени, откуда следует непрерывность угловой скорости ω. Это были случаи механической инерционности.

Энергия магнитного поля в катушке с индуктивностью L определяется выражением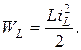

При ограниченной мощности источника напряжения энергия является непрерывной функцией времени, откуда следует непрерывность тока катушки i_L. Это магнитная инерционность. Первый закон коммутации в электрических цепях гласит: в момент коммутации ток катушки не изменяется скачком или предел тока слева равен пределу справа по времени.

Энергия электрического поля в конденсаторе с емкостью С определяется выражением

При ограниченной мощности источника тока энергия является непрерывной функцией времени, откуда следует непрерывность напряжения конденсатора u_C. Это электрическая инерционность. Второй закон коммутации в электрических цепях гласит: в момент коммутации напряжение конденсатора не изменяется скачком, или предел напряжения слева равен пределу справа по времени.

Тепловая энергия в теле с теплоемкостью С определяется выражением

Q = C θ.

При ограниченной мощности источника тепла тепловая энергия тела является непрерывной функцией времени, откуда следует непрерывность температуры тела θ. Это тепловая инерционность.

Если учитывается только магнитная инерционность, то переходный процесс называется электромагнитным. Если учитывается только механическая инерционность и влияние ЭДС вращения, то переходный процесс называется электромеханическим.

Виды теплопередачи. Электро-тепловые аналогии

Различают три основных вида теплопередачи: теплопроводностью, конвекцией и лучеиспусканием. Начнем с теплопроводности.

Рассмотрим стенку, имеющую толщину δ и площадь S. Пусть температура с одной стороны стенки равна θ₁, а с другой – θ₂, причем θ₁ > θ₂. Тогда мощность, передаваемая от более нагретой стороны стенки к менее нагретой, определяется равенством

где λ – коэффициент теплопроводности, Вт/м·ºС.

Рис. 21.1. Теплопроводность через стенку

Эту формулу можно записать в виде

Здесь тепловое сопротивление R _θ и тепловая проводимость G _θ определяются формулами

В электрических цепях закон Ома имеет аналогичный вид:

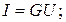
где активная проводимость G и активное сопротивление R определяются формулами

Здесь γ – удельная проводимость; ρ – удельное сопротивление; l – длина проводника; S – площадь его поперечного сечения.

Видна аналогия между тепловыми и электрическими величинами, которую можно представить следующими соотношениями.

Тепловые Электрические

величины величины

R _θ R

G _θ G

λ γ = 1/ρ

P I

θ φ

θ₁ – θ₂ U ₁₂

Отметим, что теплопередача теплопроводностью наблюдается не только через твердые тела, но и через жидкости и газы, если они неподвижны. Например, мех или поролон уменьшают теплопередачу благодаря неподвижности воздуха в их среде.

Рассмотрим теплопередачу конвекцией. Пусть имеется стенка с площадью S и с температурой поверхности θ₁, а температура воздуха на некотором расстоянии от нее θ₀. Тогда мощность тепла, передаваемого от стенки в окружающую среду, определяется выражением

где α – коэффициент теплоотдачи с единицей измерения 1 Вт/ºС·м². Здесь также можно ввести тепловую проводимость и тепловое сопротивление:

Рис. 21.2. Теплопередача конвекцией

Тогда закон Ома для теплового сопротивления имеет тот же вид:

Отметим, что в отличие от коэффициента теплопроводности λ, имеющего достаточно стабильное значение для определенного материала, коэффициент теплоотдачи α зависит от многих факторов: от формы тела, от расположения его в пространстве, от шероховатости поверхности, от размеров тела. Это связано с тем, что конвекция определяется движением газа или жидкости, которые нагреваются около горячего тела и изменяют свою плотность. Это движение подчиняется законам газодинамики или гидродинамики.

Различают свободную и принудительную конвекцию. Во втором случае используются вентиляторы или насосы для принудительного движения газа или жидкости. Имеется эмпирическая формула:

α = α₀(1 + kv),

где α₀ – коэффициент свободной теплоотдачи; k – постоянный коэффициент; v – скорость движения воздуха.

Третий вид теплопередачи – излучением наблюдается между двумя телами, разделенными прозрачной средой – твердой, жидкой или газообразной. Рассмотрим две стенки с одинаковой площадью S и с абсолютными температурами Т ₁ и Т ₂. Мощность, передаваемая от одной стенки к другой, определяется формулой

­

где k _ч – безразмерный коэффициент черноты поверхности, 0 < k _ч < 1; B – постоянная Больцмана. Постоянная Больцмана имеет единицу измерения Вт/ºК⁴м². Температура Т измеряется в градусах Кельвина и связана с температурой по Цельсию формулой:

Т = ­ θ + 273.

Для тела невыпуклой формы берут площадь ее выпуклой оболочки.

Рис. 21.3. Теплопередача излучением между двумя стенками

При изменении температуры тела следует учитывать его теплоемкость С. Это тепловая энергия, которую надо сообщить телу, чтобы его температура увеличилась на один градус. Единица измерения теплоемкости 1 Дж/ºC. Удельной теплоемкостью с называется теплоемкость одного килограмма вещества. Она измеряется в 1 Дж/кгºC.

Процессы нагревания одного и двух однородных тел. Схемы замещения

Рассмотрим процесс нагревания однородного тела, имеющего одинаковую удельную теплоемкость по всему объему и бесконечно большой коэффициент теплопроводности, так что все его точки имеют одинаковую температуру (см. рис. 21.4). Тело имеет теплоемкость С, температуру θ и мощность тепловыделения Р. Окружающая среда имеет температуру θ₀, а тепловое сопротивление между ней и телом равно R _θ.

Рис. 21.4. Нагревание однородного тела

За время от момента времени t до момента t + Δ t в теле выделится энергия

Часть ее С Δθ пойдет на нагревание тела, а вторая часть (θ – θ₀)Δ t/R _θ уйдет в окружающую среду. Запишем уравнение баланса энергии:

Отсюда получаем дифференциальное уравнение

Обозначив

получаем дифференциальное уравнение

(21.1)

Его решение имеет вид:

При начальном условии

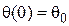
получаем

График температуры показан на рис. 21.5.

Рис. 21.5. Процесс нагревания однородного тела

На рис. 21.6 показана электрическая схема замещения, соответствующая процессу нагревания однородного тела. Источнику тепла соответствует источ-

Рис. 21.6. Электрическая схема замещения теплового процесса

ник тока P. Температуре окружающей среды соответствует источник ЭДС θ₀. Теплоемкости С соответствует конденсатор с емкостью С, а тепловому сопротивлению – резистор с сопротивлением R _θ.

Рассмотрим процесс нагревания двух однородных тел (см. рис. 21.7). Первое тело Т1 имеет теплоемкость С ₁, температуру θ₁ и мощность тепловыделения Р ₁. Второе тело Т2 имеет теплоемкость С ₂, температуру θ₂ и мощность тепловыделения Р ₂. Окружающая среда имеет температуру θ₀. Тепловое сопротивление между ней и первым телом равно R _θ1, а между ней и вторым телом – R _θ2. Тепловое сопротивление между телами – R _θ12.

Рис. 21.7. Нагревание двух однородных тел

За время от момента времени t до момента t + Δ t в теле Т1 выделится энергия

Часть ее С ₁Δθ₁ пойдет на нагревание тела, вторая часть (θ₁ – θ₀)Δ t/R _θ1 уйдет в окружающую среду. Третья часть (θ₁ – θ₂)Δ t/R _θ12 перейдет к телу Т2. Запишем уравнение баланса энергии:

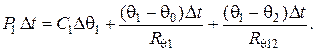
Отсюда получаем дифференциальное уравнение

За время от момента времени t до момента t + Δ t в теле Т2 выделится

энергия

Часть ее С ₂Δθ₂ пойдет на нагревание тела Т2, вторая часть (θ₂ – θ₀)Δ t/R _θ2 уйдет в окружающую среду. Третья часть (θ₂ – θ₁)Δ t/R _θ12 перейдет к телу Т1. Запишем уравнение баланса энергии:

Отсюда получаем второе дифференциальное уравнение

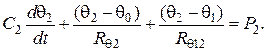(21.3)

Для решения уравнений (21.2), (21.3) нужно задать начальные условия

Отметим, что система уравнений (21.2), (21.3) имеет характеристическое уравнение с вещественными корнями, т.е. решение всегда представляет сумму экспонент (колебательный переходный процесс невозможен).

Электрическая схема замещения для процесса нагревания двух однородных тел показана на рис. 21.8. Источникам тепла соответствуют источники тока Р ₁ и Р ₂. Тепловым сопротивлениям соответствуют резисторы с сопротивлениями R _θ1, R _θ2 и R _θ12, а теплоемкостям тел – конденсаторы с емкостями С ₁и С ₂.

Рис. 21.8. Электрическая схема замещения для процесса нагревания двух тел

Тепловые режимы работы электропривода: продолжитель-кратковременный, повторно-кратковременный

Рассмотрим три основных режима работы электропривода: продолжительный, кратковременный и повторно-кратковременный. Предположим, что электродвигатель или выключен, или работает некоторое время при номинальной нагрузке.

Пусть двигатель работает такое время, что он успевает нагреться до установившейся температуры, т.е. выполняется неравенство:

t _р > 5 T _θ.

Такой режим называется продолжительным (см. рис. 22.1). Жирной линией показано время работы.

Рис. 22.1. Изменение температуры при продолжительном режиме работы

Кратковременный режим работы предполагает, что за время работы электропривода t _р двигатель не успевает нагреться до установившейся температуры, а за время паузы t _п он полностью остывает. Выполняются неравенства:

t _р < 3 T _θ; t _п > 5 T _θ.

На рис. 22.2 представлен график температуры при кратковременном режи-

ме работы. Штриховыми линиями показаны графики температуры в предположении, что двигатель включается надолго.

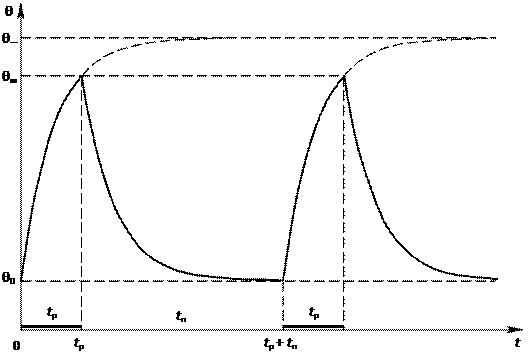
Рис. 22.2. Температура двигателя при кратковременном режиме работы

За время работы двигателя t _р он нагревается от температуры окружающей среды θ₀ до температуры θ_m < θ_∞. За время паузы t _п двигатель успевает остыть до температуры θ₀.

При повторно-кратковременном режиме работы выполняются неравенства:

t _р < 3 T _θ; t _п < 3 T _θ.

На рис. 22.3 показан график температуры при повторно-кратковременном режиме работы.

За время работы двигателя t _р он нагревается от температуры θ₁ > θ₀ до температуры θ₂ < θ_∞. За время паузы t _п двигатель остывает до температуры θ₁. Чтобы найти значения температур θ₁ и θ₂, запишем законы изменения температуры при нагревании и охлаждении:

Подставляя вместо переменной t значения t _р и t _р + t _п, получаем уравнения

(22.1)

(22.2)

Рис. 22.3. Температура двигателя при повторно-кратковременном режиме работы

Из этих уравнений можно найти предельные температуры двигателя θ₁ и θ₂. Если выполняется неравенство

t _р > t _п,

то средняя температура двигателя удовлетворяет неравенству

Потери энергии в электродвигателе. Средняя мощность потерь двигателей разных типов

Выше были рассмотрены три характерных режима работы электропривода, при которых чередуются периоды работы двигателя с номинальной нагрузкой и периоды выключенного состояния. Однако в реальных условиях момент нагрузки и скорость вращения могут меняться в значительных пределах. В таких случаях интересна средняя температура двигателя. Поскольку двигатель как нагреваемое тело может рассматриваться в виде линейного объекта, то средняя температура может быть найдена по средней мощности потерь.

Все потери мощности в двигателе можно разделить на электрические, магнитные и механические. Электрические потери возникают в обмотках статора и ротора при протекании по ним электрических токов. Мощность электрических потерь определяется по закону Джоуля-Ленца:

p _э = ri ².

Магнитные потери возникают в магнитопроводах при изменении или вращении магнитного потока. Они состоят из потерь на гистерезис и вихревые токи и определяются формулой

­

где m – масса стали; B_m – амплитуда магнитной индукции; f – циклическая частота перемагничивания; ξ, η – постоянные коэффициенты. Слагаемые в скобках соответствуют потерям на гистерезис и на вихревые токи.

Механические потери вызываются трением в опорах, трением в щеточно-коллекторном узле, аэродинамическими и вентиляционными потерями. Мощность механических потерь определяется формулой

P _мех = ω M _мех(ω).

Предположим, что электромагнитный момент двигателя изменяется по периодическому закону. Выясним, как зависит средняя мощность потерь в двигателе от закона изменения момента для двигателей различных типов. Изменение скорости вращения учитывать не будем.

У двигателя постоянного тока независимого возбуждения электромагнитный момент определяется выражением:

M = c Ф i _я.

При постоянном магнитном потоке Ф мощность электрических потерь в якоре пропорциональна квадрату электромагнитного момента:

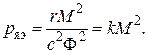
Среднее значение мощности потерь в якоре

где М _ск – среднеквадратическое значение электромагнитного момента:

Средняя температура двигателя определяется средним значением суммарной мощности потерь:

P = P ₀ + kM _ск². (22.3)

Здесь P ₀ – среднее значение мощности потерь всех других видов, кроме электрических потерь в якоре.

У двигателя постоянного тока последовательного возбуждения электромагнитный момент определяется выражением:

M = c Ф i,

где магнитный поток пропорционален току i, если он невелик и насыщение можно не учитывать:

Ф = k _Ф i.

Следовательно, электромагнитный момент связан с током равенством

M = ck _Ф i ².

Тогда мощность электрических потерь в обмотках якоря и возбуждения определяется выражениями

Среднее значение мощности электрических потерь в якоре и обмотке возбуждения

где М _ср – среднее значение электромагнитного момента:

Средняя температура двигателя последовательного возбуждения определяется средним значением суммарной мощности потерь:

P = P ₀ + kM _ср. (22.4)

Рассмотрим синхронный двигатель при постоянном магнитном потоке ротора-индуктора Ф. Его электромагнитный момент определяется выражением

M = c Ф I sin θ,

где I – действующее значение тока фазы обмотки статора: θ – угол между продольной осью ротора и вектором МДС статора.При фиксированном угле θ формула совпадает по виду с формулой момента двигателя постоянного тока независимого возбуждения. Можно сделать вывод, что средняя мощность потерь в синхронном двигателе определяется формулой (22.3).

Рассмотрим трехфазный асинхронный двигатель с короткозамкнутым ротором. Его электромагнитный момент определяется формулой (см. (9.7)):

откуда видно, что при постоянном скольжении s момент пропорционален квадрату тока статора. Ток ротора пропорционален току обмотки статора, а магнитный поток в двигателе пропорционален напряжению обмотки статора. Видно, что электрические и магнитные потери пропорциональны электромагнитному моменту. Следовательно, средняя мощность потерь в асинхронном двигателе определяется формулой (22.4).

Рассмотрим однофазный или трехфазный трансформатор. Потребляемая от него мощность пропорциональна току вторичной обмотки. Ток первичной обмотки приближенно пропорционален току вторичной обмотки. Следовательно, мощность электрических потерь в обмотках трансформатора пропорциональна квадрату потребляемой от трансформатора мощности.

Средняя температура трансформатора определяется средним значением суммарной мощности потерь:

(22.5)

или

. (22.6)

Здесь P _2ск – среднеквадратическое значение потребляемой от трансформатора мощности P ₂:

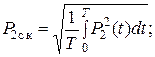
I _ск – среднеквадратическое значение действующего значения тока I ₂:

Рассмотрим электромагнит постоянного тока (см. рис. 20.3). Усилие пропорционально квадрату магнитной индукции, а без учета насыщения магнитопровода – квадрату тока обмотки:

F = ci ².

Мощность потерь в обмотке определяется равенством

p = ri ².

Следовательно, средняя температура электромагнита определяется средним значением усилия:

P = P ₀ + kF _ср, (22.7)

Средняя температура двигателя или электромагнитного устройства определяется формулой

,

где R _θ – тепловое сопротивление; θ – температура окружающей среды.

Рассмотрим электропривод с двигателем постоянного тока независимого возбуждения, который вращает объект управления по закону

α = ω₀ t + А sin Ω t, (22.8)

где ω₀ – средняя скорость вращения; А – амплитуда колебаний; Ω – угловая частота колебаний. Дифференцируя угол α, получаем

ω = ω₀ + A Ω cos Ω t, (22.9)

ε = – A Ω² sin Ω t, (22.10)

М = М _с + J ε, (22.11)

M = M _c – JA Ω² sin Ω t, (22.12)

(см. формулы (14.9 – (14.13)). Согласно выражениям (22.9), (22.12) на плоскости M – ω получается эллипс, центр которого имеет координаты M _с,ω₀. (см. рис. 22.4)

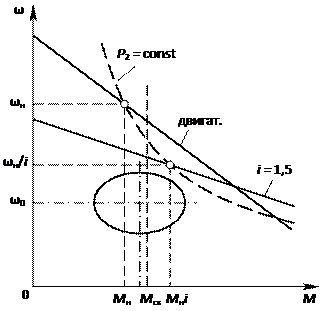
Рис. 22.4. Множество требуемых сочетаний M – ω

и механическая характеристика двигателя с редуктором

Пусть выбран двигатель с номинальными параметрами M _н и ω_н. Среднеквадратический момент электродвигателя определяется выражением

Это значение показано на рис. 22.4 вертикальной штриховой линией. Видно, что этот момент превышает номинальный момент двигателя, т.е. электродвигатель не проходит по нагреву, хотя динамика обеспечивается.

Тот же электродвигатель с редуктором, имеющим передаточное отношение i = 1,5, допускает по нагреву момент M _н i, больший среднеквадратического значения Он обеспечивает и динамику, т.е. характеристика агрегата лежит выше и правее эллипса. Штриховой линией показано множество постоянных значений мощности P ₂.

Отметим трудность выбора двигателя, связанную с тем, что момент инерции его ротора суммируется с моментом инерции объекта управления с учетом передаточного отношения редуктора.

Соотношения подобия в электроприводах. Геометрические, механические, электрические и магнитные величины

Простейшим видом подобия является геометрическое подобие. Предположим, что имеется базовый объект, размеры которого будем обозначать буквами с индексом '0'. Другой объект будем называть объектом сравнения и его размеры будем обозначать буквами без индексов.

Рассмотрим два треугольника, показанные на рис. 23.1. Базовый треугольник имеет вершины A ₀, B ₀, C ₀, а треугольник сравнения – вершины A, B, C. Одинаково расположенные точки двух объектов назовем сходственными. Фигуры называются геометрически подобными, если расстояния между их сходственными точками пропорциональны. Коэффициент пропорциональности назовем коэффициентом подобия. Для указанных треугольников имеем:

AB = γ A ₀ B ₀; BC = γ B ₀ C ₀; CA = γ C ₀ A ₀; h = γ h ₀.

Рис. 23.1. Геометрически подобные треугольники

Определяющим называется размер, выбранный для задания коэффициента подобия. Для треугольников это может быть длина основания:

l = γ l ₀ . (23.1)

Соотношение (23.1) является характерным для линейных размеров.

Площади двух подобных фигур относятся как квадраты их размеров, откуда следует:

S = γ² S ₀ . (23.2)

Объемы двух подобных тел относятся как кубы их размеров, откуда имеем

V = γ³ V ₀ . (23.3)

На рис. 23.2 показаны две подобные пирамиды. За определяющий размер может быть принята высота пирамиды:

h = γ h ₀

Рис. 23.2. Подобные пирамиды

В некоторых случаях пространство можно представить как прямое произведение подпространств меньшей размерности, в каждом из которых имеется свой коэффициент подобия. Такое подобие называется аффинным. Например, пусть два цилиндра имеют разные диаметры и осевую длину, причем выполняются равенства:

d = γ₁ d ₀ , l = γ₂ l ₀ .

Тогда для объемов этих цилиндров справедливо равенство:

V = γ₁² γ₂ V ₀ . (23.4)

Для масс геометрически подобных тел справедливо равенство:

, (23.5)

где ρ₀ – плотность материала базового тела; ρ – плотность тела сравнения.

Осевой момент инерции тела с двумя закрепленными точками определяется интегралом

где r – расстояние от элемента массы dm до оси вращения. Видно, что при полном подобии тел имеет место равенство

(23.6)

При аффинном подобии формула изменяется:

(23.7)

Видно, что при увеличении диаметра цилиндра в два раза момент инерции возрастает в 16 раз.

Важной составной частью электропривода является электродвигатель, имеющий ряд электрических и магнитных параметров. Рассмотрим сначала электрические величины.

Активное сопротивление проводника с длиной l и с постоянным сечением S определяется по формуле:

где ρ – удельное сопротивление.

Рассмотрим два геометрически подобных проводника, выполненных из различных материалов. Их активные сопротивления удовлетворяют равенству

(23.8)

а при аффинном подобии

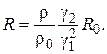(23.9)

Для активной проводимости имеем обратные формулы. При полном геометрическом подобии

(23.10)

а при аффинном подобии

(23.11)

Электрический ток I и напряжение U определяются формулами

(23.12)

(23.13)

где E – напряженность электрического поля; j – плотность тока; E = ρ j.

Емкость конденсатора С может быть определена по формуле

где S – площадь одной пластины конденсатора; δ – расстояние между пластинами; ε – диэлектрическая проницаемость материала между пластинами. Получаем формулу для емкости:

(23.14)

Обмотка с числом витков w и током I создает магнитодвижущую силу

F = wI.

Эту формулу желательно преобразовать, чтобы в нее входили линейные размеры и плотность тока:

F = k _з.м bhj,

где k _з.м – коэффициент заполнения поперечного сечения катушки медью; b, h – ширина и толщина катушки; j – плотность тока. Отсюда следует, что при подобии двух катушек справедлива формула:

(23.15)

При протекании тока по катушке в ней выделяется мощность в виде тепла. Эта мощность определяется по закону Джоуля-Ленца:

P=RI ².

Активное сопротивление катушки и ток даются выражениями

,

где S – площадь сечения проводника по меди; j – плотность тока; l _ср – средняя длина одного витка катушки.

Подставляя эти выражения в формулу мощности Р, получаем формулу

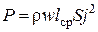
или

P = ρ j ² V _м,

где V _м – объем меди катушки.

Если имеются две геометрически подобные катушки, то для мощности потерь имеем формулу

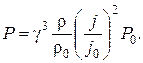(23.16)

Рассмотрим теперь магнитные величины.

Магнитное сопротивление ферромагнитного стержня длиной l и с постоянным сечением S определяется по формуле:

где μ – магнитная проницаемость стержня.

Рассмотрим два геометрически подобных стержня, выполненных из различных материалов. Их магнитные сопротивления удовлетворяют равенству

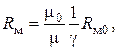(23.17)

а при аффинном подобии

(23.18)

Для магнитной проводимости Λ имеем обратные формулы. При полном геометрическом подобии

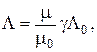(23.19)

а при аффинном подобии

(23.20)

Магнитный поток Ф и магнитное напряжение U _м определяются формулами

(23.21)

(23.22)

где Н – напряженность магнитного поля, H = B/ μ.

Индуктивность катушки L определяется формулами

Здесь w – число витков катушки. Отсюда получаем формулу

(23.23)

Как видно, без числа витков здесь не обойтись.

Мощность потерь в стали (магнитных потерь) определяется формулой

где P _в.т, P _г – мощности потерь на вихревые токи и гистерезис; ξ, η – постоянные коэффициенты; B_m – амплитуда магнитной индукции; f – частота перемагничивания; V _c – объем стали.

Отсюда следует, что мощности потерь в геометрически подобных магнито-проводах при одинаковой частоте связаны соотношением

(23.24)

Отметим, что формулы (23.8) – (23.11) похожи на формулы (23.17) – (23.20), формулы (23.12) – (23.13) похожи на формулы (23.21) – (23.22), формула (23.14) похожа на формулу (23.23), а формула (23.16) похожа на формулу (23.24).

Обратимся теперь к теплопроводности. При теплопередаче теплопровод-ностью имеет место формула:

где λ – коэффициент теплопроводности; S – площадь стенки;δ – ее толщина; θ₁ и θ₂ – температура стенки с двух сторон. Эту формулу можно записать в виде

Здесь тепловое сопротивление R _θ и тепловая проводимость G _θ определяются формулами Здесь тепловое сопротивление R _θ и тепловая проводимость G _θ определяются формулами

При полном геометрическом подобии получаем соотношения:

При теплопередаче конвекцией имеет место формула:

где α – коэффициент теплоотдачи; S – площадь стенки;θ₁ и θ₀ – температура стенки и температура воздуха на некотором расстоянии от стенки. Эту формулу можно записать в виде

Здесь тепловое сопротивление R _θ и тепловая проводимость G _θ определяются формулами

При полном геометрическом подобии получаем соотношения:

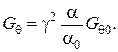
Отметим, что сам коэффициент теплоотдачи зависит от размеров тела.

Коснемся кратко вопроса подобия динамических процессов в электроприводах. Пусть имеется базовый электропривод постоянного тока. При подаче на обмотку якоря напряжения U ₀ его скорость вращения изменяется по закону ω₀(t ₀). Имеется электропривод постоянного тока сравнения. При подаче на обмотку якоря