Градиентные методы. Понятие градиента и его вычисление. Разновидности градиентных методов.

1. Понятие градиентных методов. Необходимым условием существова­ния экстремума непрерывной дифференцируемой функции яв­ляются условия вида

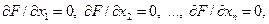
где – аргументы функции. Более компактно это условие можно записать в форме

(2.4.1)

где – обозначение градиента функции в заданной точке.

Методы оптимизации, использующие при определении экстремума целе­вой функции градиент, называются градиентными. Их широко применяют в системах оптимального адаптивного управления установившимися состояния­ми, в которых производится поиск оптимального (в смысле выбранного крите­рия) установившегося состояния системы при изменении ее параметров, струк­туры или внешних воздействий.

Уравнение (2.4.1) в общем случае нелинейно. Непосредственное решение его либо невозможно, либо весьма сложно. Нахождение решений такого рода уравнений возможно путем организации специальной процедуры поиска точки экстремума, основанной на использовании различного рода рекуррентных фор­мул.

Процедура поиска строится в форме многошагового процесса, при кото­ром каждый последующий шаг приводит к увеличению или уменьшению целе­вой функции, т. е. выполняются условия в случае поиска максимума и миниму­ма соответственно:

Через n и n– 1 обозначены номера шагов, а через и – векторы, соответствующие значениям аргументов целевой функции на n -м и (п– 1)-м шагах. После r-го шага можно получить

т. е. после r - шагов - целевая функция уже не будет увеличиваться (уменьшать­ся) при любом дальнейшем изменении ее аргументов;. Последнее означает достижение точки с координатами для которой можно написать, что

	(2.4.2)
	(2.4.3)

где – экстремальное значение целевой функции.

Для решения (2.4.1) в общем случае может быть применена следующая процедура. Запишем значение координат целевой функции в виде

(2.4.4)

где – некоторый коэффициент (скаляр), не равный нулю.

В точке экстремума так как

Решение уравнения (2.4.1) этим способом возможно, если выполняется условие сходимости итерационного процесса для любого начального значения.

Методы определения , основанные на решении уравнения (2.2.), отли­чаются друг от друга выбором , т. е. выбором шага изменения целевой функции в процессе поиска экстремума. Этот шаг может быть постоянным или переменным Во втором случае закон изменения зна­чения шага, в свою очередь, может, быть заранее определен или. зависеть от те­кущего значения (может быть нелинейным).

2. Метод наискорейшего спуска. Идея метода наискорейшего спуска со­стоит в том, что поиск экстремума должен производиться в направлении наи­большего изменения градиента или антиградиента, так как это путь – наикрат­чайший для достижения экстремальной точки. При его реализации, в первую очередь, необходимо вычислить градиент в данной точке и выбрать значение шага.

Вычисление градиента. Так как в результате оптимизации находятся координаты точки экстремума, для которых справедливо соотношение:

то вычислительную процедуру определения градиента можно заменить процедурой определения составляющих градиентов в дискретных точках пространства целевой функции

	(2.4.5)

где – малое изменение координаты

Если предположить, что точка определения градиента находится посередине

отрезка то

(2.4.5)

Выбор (2.4.5) или (2.4.6) зависит от крутизны функции на участке - Ах;; если крутизна не велика, предпочтение следует отдать (2.4.5), так как вычислений здесь меньше; в противном случае более точные результаты дает вычисление по (2.4.4). Повышение точности определения градиента возможно также за счет усреднения случайных отклонений.

Выбор значения шага Сложность выбора значения шага состоит в том, что направление градиента может меняться от точки к точке. При этом слишком большой шаг приведёт к отклонению от оптимальной траектории, т. е. от направления по градиенту или антиградиенту, а слишком малый шаг -к очень медленному движению к экстремуму за счет необходимости выполнения большого объёма вычислений.

Одним из возможных методов оценки значения шага является метод Ньютона – Рафсона. Рассмотрим его на примере одномерного случая в предположении, что экстремум достигается в точке, определяемой решением уравнения (рис.2.4.2).

Пусть поиск начинается из точки причем в окрестностях этой точки функция разложима в сходящийся ряд Тейлора. Тогда

(2.4.7)

Направление градиента в точке совпадает с направлением касательной. При поиске минимальной экстремальной точки изменение координаты х при движении по градиенту можно записать в виде:

(2.4.8)

Рис.2.4.2 Схема вычисления шага по методу Ньютона – Рафсона.

Подставив (2.4.7) в (2.4.8), получим:

Так как по условию данного примера значение достигается в точке, определяемой решением уравнения то можно попытаться сделать такой шаг, чтобы т. е. чтобы

откуда

Подставим новое значение в целевую функцию. Если то в точке процедура определения повторяется, в результате чего находится значение:

и т.д. вычисление прекращается, если изменения целевой функции малы, т. е.

где – допустимая погрешность определения целевой функции.

Оптимальный градиентный метод. Идея этого метода заключается в следующем. В обычном методе наискорейшего спуска шаг выбирается в общем случае [когда ] произвольно, руководствуясь лишь тем, что он не должен превышать определенного значения. В оптимальном градиентном методе значение шага выбирается исходя из требования, что из данной точки в направлении градиента (антиградиента) следует двигаться до тех пор, пока целевая функция будет увеличиваться (уменьшаться). Если это требование не выполняется, необходимо прекратить движение и определить новое направление движения (направление градиента) и т. д. (до нахождения оптимальной точки).

Таким образом, оптимальные значения и для поиска минимума и максимума соответственно определяются из решения уравнений:

(1)

(2)

В (1) и (2) соответственно

Откуда

Следовательно определение на каждом шаге заключается в нахождении из уравнений (1) или (2) для каждой точки траектории движения вдоль градиента, начиная с исходной.

Основной недостаток оптимального градиентного метода – необходимость решения уравнения (1) для определения на каждом шаге оптимального значения При большой размерности задачи и сложном виде целевой функции это решение достаточно сложно и требует большого расхода машинного времени.

Возможен другой метод получения не требующий решения уравнения (1). Он основывается на следующей процедуре. Наибольшее значение шага из исходной точки Х[к] находится по методу Ньютона – Рафсона.

Обозначим через номера шагов, соответствующие возможным попыткам движения вдоль градиента с шагом, уменьшенным вдвое по сравнению с Тогда каждое изменение шага можно записать а виде:

Значение целевой функции определяется как:

Затем шаг уменьшается вдвое и находится новое значение целевой функции:

Если в результате образовалось неравенство:

то следует продолжить уменьшение шага в два раза вдоль градиента до выполнения условия:

Полученное значение следует сравнить с целевой функцией полученной при вычислении k- го шага.

Если то процедуру уменьшения шага вдвое следует продолжать до получения значения

После этого необходимо восстановить предыдущие полшага, запомнить сделать шаг. Зная значение можно определить координаты -й точки и значение целевой функции в этой точке и т. д.

Вычисления заканчиваются, когда разность между значениями целевойфункции двух соседних шагов будет меньше или равна определяющей точность вычисления целевой функции, а следовательно, и точность управления.

Date: 2016-07-18; view: 1409; Нарушение авторских прав