Методы дифференциального и вариационного исчислений. Условия применения методов. Понятие функционала.

1. Отыскание экстремальных значений целевой функции методами диф­ференциального исчисления возможней только в том случае, если целевая функ­ция дифференцируема и при этом, что особенно существенно, отсутствуют ог­раничения.

Если целевая функция Z представляет собой функцию многих пе­ременных , то необходимо решить систему

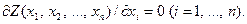
Однако это трудоемко и не обеспечивает гарантированного решения. Этим способом нельзя найти максимум, если он лежит не внутри, а на границе исследуемой области. При большом числе переменных – проектных параметров задача становится практически неразрешимой. Необходимые условия примене­ния методов дифференциального исчисления к задачам оптимизации сводятся к следующему: исследуемый процесс должен быть одношаговым; целевая функ­ция должна быть дифференцируемой по всем переменным, хотя бы двукратно; ограничения на решение отсутствуют.

2. Методы вариационного исчисления являются обобщением методов дифференциального исчисления на случаи бесконечного числа переменных. Они позволяют найти экстремальное значение функционалов, т.е. функции, аргумент которой также функция. Если в выражении для целевой функции число переменных становится бесконечно большим, то это выражение можно записать как где t – непрерывная переменная. В этом случае функция рассматривается в качестве бесконечномерного аналога переменных

Задание функционала равносильно заданию закона, по которому каждой функции из некоторого класса ставится в соответствие определен­ное число

В функционале значение интеграла, т.е. действительное число, ставится в соответствие каждой интегрируемой функции из данного класса функций.

Простейшая задача вариационного исчисления, называемая также i пер­вой или фундаментальной задачей, состоит в нахождении экстремума функцио­нала вида

Для того чтобы функция обращала функционал К в максимум или минимум, необходимо, чтобы она удовлетворяла уравнению Эйлера:

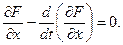
Однако даже в этом простейшем случае уравнение решается не всегда.

Для решения вариационных задач используются прямые и непрямые ме­тоды. Сущность последних состоит в сведении вариационной задачи к исследо­ванию дифференциального уравнения или системы уравнений. Прямые методы заключаются в построении минимизирующей последовательности функций (кривых) таких, что где – экстремум К; кроме того, необходимы доказательства, что у этой последовательности существует пре­дельная кривая и предельный переход

Необходимые условия применения методов вариационного исчисления к задачам оптимизации: наличие аналитического выражения для целевой функ­ции; непрерывность и дифференцируемость этой функции; отсутствие ограни­чений.

Date: 2016-07-18; view: 636; Нарушение авторских прав