
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства математического ожидания.
|
|
1. Математическое ожидание постоянной равно самой постоянной:
М (С) = С.
2. Постоянный множитель можно выносит за знак математического ожидания: М (СХ) = С М (Х).
Тогда М (СХ) = Сх 1 р 1 + Сх 2 р 2 + … + Схпрп = С (х 1 р 1 + х 2 р 2 + … + хпрп) = СМ (Х).
Определение Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая. В противном случае случайные величины зависимы.
Определение Назовем произведением независимых случайных величин Х и Y случайную величину XY, возможные значения которой равны произведениям всех возможных значений Х на все возможные значения Y, а соответствующие им вероятности равны произведениям вероятностей сомножителей.
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
M (XY) = M (X) M (Y). Следовательно, M (XY) = x 1 y 1· p 1 g 1 + x 2 y 1· p 2 g 1 + x 1 y 2· p 1 g 2 + x 2 y 2· p 2 g 2 = y 1 g 1(x 1 p 1 + x 2 p 2) + + y 2 g 2(x 1 p 1 + x 2 p 2) = (y 1 g 1 + y 2 g 2) (x 1 p 1 + x 2 p 2) = M (X)· M (Y).
Замечание 1. Аналогично можно доказать это свойство для большего количества возможных значений сомножителей.
Замечание 2. Свойство 3 справедливо для произведения любого числа независимых случайных величин, что доказывается методом математической индукции.
Определение Определим сумму случайных величин Х и Y как случайную величину Х + Y, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением Y; вероятности таких сумм равны произведениям вероятностей слагаемых (для зависимых случайных величин – произведениям вероятности одного слагаемого на условную вероятность второго).
4. Математическое ожидание суммы двух случайных величин (зависимых или независимых) равно сумме математических ожиданий слагаемых: M (X + Y) = M (X) + M (Y).
Значит, M (X + Y) = x 1 p 1 + x 2 p 2 + y 1 g 1 + y 2 g 2 = M (X) + M (Y).
Замечание. Из свойства 4 следует, что сумма любого числа случайных величин равна сумме математических ожиданий слагаемых.
Пример. Найти математическое ожидание суммы числа очков, выпавших при броске пяти игральных костей.
Найдем математическое ожидание числа очков, выпавших при броске одной кости: М (Х 1) = (1 + 2 + 3 + 4 + 5 + 6) 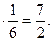 Тому же числу равно математическое ожидание числа очков, выпавших на любой кости. Следовательно, по свойству 4 М (Х)=
Тому же числу равно математическое ожидание числа очков, выпавших на любой кости. Следовательно, по свойству 4 М (Х)= 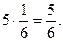
Дисперсия.
Для того, чтобы иметь представление о поведении случайной величины, недостаточно знать только ее математическое ожидание. Рассмотрим две случайные величины: Х и Y, заданные рядами распределения вида
| Х | |||
| р | 0,1 | 0,8 | 0,1 |
| Y | ||
| p | 0,5 | 0,5 |
Найдем М (Х) = 49·0,1 + 50·0,8 + 51·0,1 = 50, М (Y) = 0·0,5 + 100·0,5 = 50. Как видно, математические ожидания обеих величин равны, но если для Х М (Х) хорошо описывает поведение случайной величины, являясь ее наиболее вероятным возможным значением (причем остальные значения ненамного отличаются от 50), то значения Y существенно отстоят от М (Y). Следовательно, наряду с математическим ожиданием желательно знать, насколько значения случайной величины отклоняются от него. Для характеристики этого показателя служит дисперсия.
Определение Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания: D (X) = M (X – M (X))².
Пример.
Найдем дисперсию случайной величины Х (числа стандартных деталей среди отобранных) в примере 1 данной лекции. Вычислим значения квадрата отклонения каждого возможного значения от математического ожидания:
(1 – 2,4)2 = 1,96; (2 – 2,4)2 = 0,16; (3 – 2,4)2 = 0,36. Следовательно,

Замечание 1. В определении дисперсии оценивается не само отклонение от среднего, а его квадрат. Это сделано для того, чтобы отклонения разных знаков не компенсировали друг друга.
Замечание 2. Из определения дисперсии следует, что эта величина принимает только неотрицательные значения.
Замечание 3. Существует более удобная для расчетов формула для вычисления дисперсии, справедливость которой доказывается в следующей теореме:
Теорема D(X) = M (X ²) – M ²(X). Доказательство.
Используя то, что М (Х) – постоянная величина, и свойства математического ожидания, преобразуем формулу (7.6) к виду:
D (X) = M (X – M (X))² = M (X ² - 2 X·M (X) + M ²(X)) = M (X ²) – 2 M (X)· M (X) + M ²(X) =
= M (X ²) – 2 M ²(X) + M ²(X) = M (X ²) – M ²(X), что и требовалось доказать.
Пример. Вычислим дисперсии случайных величин Х и Y, рассмотренных в начале этого раздела. М (Х) = (492·0,1 + 502·0,8 + 512·0,1) – 502 = 2500,2 – 2500 = 0,2.
М (Y) = (02·0,5 + 100²·0,5) – 50² = 5000 – 2500 = 2500. Итак, дисперсия второй случайной величины в несколько тысяч раз больше дисперсии первой. Таким образом, даже не зная законов распределения этих величин, по известным значениям дисперсии мы можем утверждать, что Х мало отклоняется от своего математического ожидания, в то время как для Y это отклонение весьма существенно.
Свойства дисперсии.
1) Дисперсия постоянной величины С равна нулю: D (C) = 0.
2) Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат: D (CX) = C ² D (X).
3) Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D (X + Y) = D (X) + D (Y).
Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме их дисперсий.
Следствие 2. Дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины.
4) Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D (X – Y) = D (X) + D (Y).
Дисперсия дает среднее значение квадрата отклонения случайной величины от среднего; для оценки самого отклонения служит величина, называемая средним квадратическим отклонением.
ОпределениеСредним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии:  .
.
Пример. В предыдущем примере средние квадратические отклонения Х и Y равны соответственно 
Date: 2016-07-18; view: 486; Нарушение авторских прав