
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

МЕТОД КОРРЕЛЯЦИОННО-РЕГРЕССИОННОГО
|
|
АНАЛИЗА
Метод корреляционного и регрессионного анализа широко используется для определения тесноты связи между показателями, не находящимися в функциональной зависимости. Теснота связи между изучаемыми явлениями измеряется корреляционным отношением (для криволинейной зависимости). Для прямолинейной зависимости исчисляется коэффициент корреляции.
Одной из распространенных аналитических задач, решаемых с применением корреляционно метода, является задача на запуск-выпуск. Допустим, что имеются фактические данные о запуске и выпуске промышленных изделий (в тыс. шт.).

Требуется определить зависимость выпуска изделий в среднем от их запуска, составив соответствующее уравнение регрессии. По исходным данным построим в системе координат точки, соответствующие значениям переменных х и у. Проведем линию теоретической зависимости между показателями (рис.4).

Рис. 4. Линия регрессии
Значения 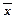 и
и  определяются по формулам:
определяются по формулам:

Дальнейшим вычислениям придается табличная форма

Теснота связи между показателями запуска и выпуска измеряется коэффициентом корреляции, который исчисляется по формуле

Подставляя соответствующие значения, получим:
выборочные средние квадратические отклонения


ковариация

парный коэффициент корреляции

Считая формулу связи линейной (у = а 0 + а 1 х) определим зависимость выпуска промышленных изделий от их запуска. Для этого решается система нормальных уравнений:


Величины Σxi 2 и Σxiyi представлены в следующей таблице

Значение а 0 определяем из первого уравнения:
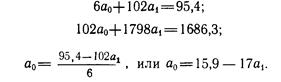
Подставляя найденное выражение а 0 во второе уравнение, находим значение а 1:

Итак, уравнение регрессии в окончательном виде получило следующий вид:

Проверка:

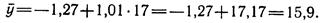
Коэффициент корреляции: 
Варианты заданий.
По данным, представленным по вариантам, построить графическую зависимость между двумя показателями, определить уравнение регрессии и коэффициент корреляции. Проанализировать полученные результаты.
Вариант 1.
Известны данные о количестве слесарей-ремонтников на машиностроительных заводах и данные о количестве станко-смен.
| Количество слесарей-ремонтников | 37 18 23 36 44 73 56 48 143 207 |
| Количество станкосмен 1000 ед. | 0,8 0,5 0,8 0,8 0,8 2,2 1,4 2,3 6,4 6,3 |
Вариант 2
В таблице приведены данные о численности работников по предприятиям.
| Предприятие | Среднее годовое число работников | Общая сумма производственных затрат |
Вариант 3
В таблице приведены данные анализа зависимости себестоимости 1 тонны угля от среднемесячной производительности труда рабочего на шахтах-комбинатах
| Среднемесячная производительность рабочего, м | 21 24 28 30 34 35 36 39 40 |
| Себестоимость 1 т угля, ден.ед | 2,0 1,3 1,2 1,3 1,1 1,1 1,0 1,1 1,0 |
Вариант 4
В таблице приведены данные о численности работников по предприятиям.
| Предприятие | Среднее годовое число работников | Общая сумма производственных затрат |
Вариант 5
Имеются данные по объему выпускаемой продукции и ее себестоимости.
| Объем выпускаемой продукции, тыс.шт | ||||||||||
| Себестоимость, ден.ед | 3,9 | 2,8 | 4,8 | 3,0 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,7 |
Вариант 6
В таблице приведены данные о численности работников по предприятиям.
| Предприятие | Среднее годовое число работников | Общая сумма производственных затрат |
Вариант 7
В таблице приведены данные по выработке на одного работающего и фондовооружённость. Определить уравнение связи и корреляционное отношение.
| Предприятие | Фондовооруженность, ден.ед./чел | Выработка на 1 работающего, ден.ед./чел |
| 1,9 2,0 2,2 2,3 2,4 2,4 2,6 2,6 2,6 | 3,3 4,6 3,4 5,5 4,0 5,1 3,0 4,2 3,8 |
Вариант 8
В таблице приведены данные о численности работников по предприятиям связи.
| Предприятие | Среднее годовое число работников | Общая сумма производственных затрат |
Вариант 9
Известны данные о количестве слесарей-ремонтников на машиностроительных заводах и данные о количестве единиц ремонтной сложности.
Данные приведены в таблице.
| Количество слесарей-ремонтников | 37 18 23 36 44 73 56 48 143 207 |
| Количество единиц ремонтной сложности 1000 ед. | 3,1 3,5 3,5 4,4 4,9 6,1 6,8 10,4 18,4 19,6 |
Вариант 10.
В таблице приведены данные о численности работников по предприятиям.
| Предприятие | Среднее годовое число работников | Общая сумма производственных затрат |
Date: 2016-07-18; view: 309; Нарушение авторских прав