Организация поиска дефектов

Основной задачей рациональной организации поиска де­фекта является сокращение времени и средств, затрачиваемых на поиск. Это возможно лишь при использовании наиболее со­вершенных программ поиска дефекта. В основном реализация операций по­иска осуществляется с помо­щью тестов. Практическая реализация те­ста состоит в подаче на вход (входы) элементов ОД воз­действий, имитирующих рабочие сигналы, и контроле реакций на эти сигналы. При этом система выводится из эксплуатации. Предполагается, что исправному состоянию элемента (узла, блока) соответствует наличие сигнала 1 на его выходе, неис­правному 0— его отсутствие. При таком способе поиска, как правило, предполагается: известны контролируемые параметры (элементы) и формы проявления отказов; отказ одного из эле­ментов влечет за собой потерю работоспособности ОД; изве­стны экономические характеристики, сопровождающие поиск; подавляющая часть ОД допускает контроль с помощью введе­ния в них контролирующего сигнала.

Среди множества критериев следует выделить две группы: критерии информа­ционные и экономические. Физическая интерпретация экономи­ческих критериев довольно разнообразна: стоимость проверки или проверочного оборудования, время поиска, число контро­лируемых элементов, средние потери на решение задачи и т. п.

При использовании тестов стремятся к получению мини­мального числа тестовых воздействий, при которых может быть обнаружен дефект любого из элементов системы, т. е. наимень­шего числа проверок (тестов). Нахождению тестов для той или иной системы предшествует анализ ее функциональной модели, графическое изображение схемы объекта и построение таблицы неисправностей.

Простейшая схема ОД представлена на рис.37, на котором обозначены: a,b,c,d — элементы объекта с соответствующими связями; S₁ и S₂ — входы; В и D — вы­ходы. Таблица неис­правностей этой схемы может быть представлена в виде таблице 4.1, в которой П обозна­чает множество всех возможных проверок, а Е — множество возможных состояний.

Таблица 4.1.

Из таблицы следует, что пять возможных состояний ОД, определяемых состоянием элементов, оказываются полностью различимыми с помощью четырех проверок. Отказавшие эле­менты определяются соответственно кодовыми числами 0011, 1011, 1000, 1110.

С ростом числа элементов увеличивается число состояний ОД, а следовательно, и сложность получения оптимальной про­граммы (минимального теста). Минимизация программ может осуществляться известными в теории булевой алгебры мето­дами.

Рассмотренный способ построения и оптимизации программ поиска дефекта особенно эффективен при диагностировании объектов дискретных систем.

Предположение о равнозначности отказов, что эквивалентно предположению об основной, или последовательной, схеме со­единений, дает возможность использовать и другие методы по­строения квазиоптимальных программ поиска дефекта. К та­ким программам относятся программы, полученные по методу половинного разбиения.

Рассмотрим особенности этого метода.

Для системы из N последовательно соединенных элементов введем параметры оценки программ поиска дефекта: - сред­нее время проверки i -го элемента; - вероятность отказа си­стемы из-за отказа i -го элемента.

Величина определяется как вероятность отказа системы при отказе i -го элемента

(4.7)

где – вероятность безотказной работы i -го элемента; 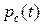– вероятность безотказной работы системы; 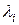– интен­сивность отказов i- го элемента; – интенсивность отказов си­стемы.

При малых значениях и выражение (4.7) приближенно может быть представлено в виде

(4.8)

Задача по поиску неисправного элемента состоит в нахож­дении такой последовательности проверок, при которой на по­иск дефекта затрачивается минимум времени.

Рассмотрим методику построения программы поиска де­фекта при одинаковых значениях и . Разделим условно си­стему на две части, содержащих соответственно m и N-m эле­ментов. Неисправный элемент с вероятностью может находиться в цепочке из m элементов и с вероятностью — в цепочке из N-m элементов.

Математическое ожидание числа неисправных элементов ле­вее и правее точки деления равно

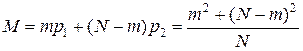(4.9)

Функция (4.9) имеет минимум, т. е. существует такое число m, при котором число неисправных элементов слева и справа от точки деления минимально. Число m, при котором достига­ется минимум математического ожидания М, а следовательно, и минимум проверок системы, находится из выражения

, (4.10)

в результате m=N/2.

Очевидно, что при этом и , т.е. отказавший элемент с равной вероятностью может находиться как в левой, так и в правой части системы.

Таким образом, при сформулированных условиях, оптималь­ный порядок проведения проверок состоит в последовательном делении цепочки элементов пополам. Направление деления каждый раз определяется результатом, полученным в точке де­ления. При различных и вероятность неисправности при проверке i- го элемента составит

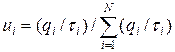(4.11)

Для нахождения оптимальной программы поиска дефекта найдём минимум математического ожидания числа несправных элементов левее и правее некоторой точки разбиения множества элементов на две части k=m. Математическое ожидание в этом случае равно

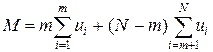
или

,

где 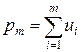- вероятность нахождения неисправных элементов левее точки m, - вероятность нахождения неисправных элементов правее точки m.

Эти вероятности составляют полную группу несовместных событий

(4.12)

Минимум будет иметь место при

В результате

(4.13)

Решая совместно уравнения (4.12) и (4.13), найдем:

(4.14)

Оптимизация программы поиска дефекта состоит в том, что при первом шаге вся цепочка элементов разбивается на две части так, чтобы с вероятностью 0.5 неисправный элемент на­ходился левее или правее некоторой контрольной точки m. В этой точке производится контроль состояния левой или пра­вой цепочки элементов. Наличие или отсутствие сигнала опре­деляет направление последующего деления на отрезки той или иной половины цепочки (с равными значениями вероятностей указанных отрезков цепи элементов). Дальнейшее развитие этой идеи нашло воплощение в разработке теории и практики метода функциональных проб. В основе его лежат положе­ния теории графов, теории групп и комбинаторного анализа. Метод открывает одно из направлений функциональной диагно­стики с элементарными тестами и предполагает использование в качестве критерия поиска индекса предшествования, т. е. разбиение пространства состояний систем с учетом их струк­турных особенностей.

При создании новых совершенных автоматических систем и автоматизированных комплексов наиболее разумным следует считать решение, при котором учет задач диагностики осуществляется на стадии проектирования. Это обусловлено интере­сами повышения эффективности САУ, а также тем выигрышем, который достигается за счет использования результатов иссле­дования качества проектируемых систем для нужд диагно­стики.

Для большинства проектируемых систем характеристики надежности имеют низкую достоверность даже в том случае, когда при проектировании используются элементы, значение показателей надежности которых известно. Последнее объясня­ется тем, что статистические данные, полученные при опреде­ленных режимах эксплуатации элементов и систем, не всегда или не в полной мере достоверны для других (отличных от ука­занных) режимов работы.

Наиболее объективными характеристиками, удовлетворяю­щими сформулированным выше задачам поиска дефекта, явля­ются относительные веса контролируемых параметров. Весовые константы содержат объективную и объемную информацию относительно надежностных свойств и структурных особенно­стей САУ и ее составляющих.

С этой целью необходимо элементы САУ рассматривать с позиций их информационных свойств. Такая аналогия имеет известное допущение, тем не менее для широкого класса САУ она правомерна. В большей степени она применима к электро­механическим и к радиоэлектронным дискретным (цифровым) и непрерывным системам.

Взаимосвязь между энергией и информацией может быть выражена соотношением

, (4.15)

где W — энергетический показатель качества элемента; — энергетический коэффициент полезного действия элемента; — пороговое (предельное) значение энергии, характеризующее максимально возможную чувствительность элемента к повыше­нию качества; — коэффициент, определяющий информацион­ные свойства элемента.

Как показывает опыт эксплуатации, совершенствование каче­ственных показателей САУ неминуемо (при постоянном значе­нии ) влечет за собой снижение остальных. Одним из таких показателей и является показатель информационных свойств элемента. Этот показатель определяется вероятностными ха­рактеристиками, в частности, он может быть выражен через показатели надежности.

Это положение неплохо согласуется с данными получен­ными при проектировании и эксплуатации систем и устройств. Действительно, повышение качественных показателей (точно­сти, быстродействия и пр.) и функциональное совершенствова­ние элементов и устройств неминуемо приводит к увеличению числа деталей и усложнению связей между ними. Так, напри­мер, для измерительных устройств известно, что затрачиваемое число деталей N в среднем пропорционально показателю их ка­чества η. Взаимосвязь между этими показателями может быть охарактеризована выражением

(4.16)

где k характеризует эффективность схем, в которых использу­ются детали.

Усложнение элементов и устройств приводит к сокращению времени наработки до отказа . В самом деле, средняя интен­сивность отказов устройства при m разновидностях деталей, входящих в него и имеющих интенсивность отказов l_i, составит

, (4.17)

где - процентное содержание каждой детали в устройстве.

Среднее время безотказной работы в этом случае определя­ется выражением

(4.18)

от которого после подстановки приходим к соотношению

(4.19)

Из (6.19) следует, что одновременное повышение надежно­сти и качественных характеристик устройства может быть до­стигнуто лишь путем применения более надежных деталей (уменьшением l_ср) и наиболее эффективных схем их использо­вания (уменьшением N). Поскольку технологические возмож­ности ограничены существующим уровнем науки и производ­ства, повышение качества устройств сопровождается уменьше­нием их надежности.

Несмотря на ограниченность статистических данных, на ос­нове которых строятся приведенные выше доказательства взаи­мосвязи качества и надежности, их можно считать в опреде­ленной степени справедливыми, тем более что такой подход, будучи использованный в практике исследования, проектирова­ния и эксплуатации систем и устройств, находит все большее подтверждение.

Анализ САУ показывает, что для выполнения наиболее су­щественных функций в ней, как правило, требуются элементы и устройства с наиболее сложной структурой. Сложность, в свою очередь, непосредственно связана с относительным весом параметров, характеризующих устройства и элементы САУ. По мере уменьшения разнообразия соединений (схем) и деталей указанная зависимость приближается к линейной. Естественно, чем проще организована сложная структура, тем меньше приблизительность взаимосвязи относительного веса контролируемых параметров и показателей надежности уст­ройств и элементов САУ.

Таким образом, учет относительного веса контролируемых параметров при построении программы поиска дефекта любых систем позволяет не только удовлетворить специфические тре­бования диагностирования САУ (классификация характера не­исправности, исключение возможных ее последствий, определе­ние и реализация тактики переключений и пр.), но и является органически необходимым для систем с ограниченным числом отказов.

Относительный вес i -го контролируемого параметра может быть определен модулем его изменения

(4.20)

причём

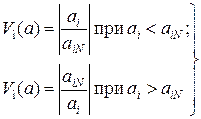(4.21)

где – значение контролируемого i -го параметра; – на­чальное значение контролируемого i -го параметра; – номи­нальное значение контролируемого i -го параметра.

Наиболее объективной характеристикой работоспособности САУ является их точность. Показателями характера изме­нения работоспособности системы диагностирования служат весовые соотношения контролируемых параметров, определяю­щие степень влияния дефекта на работоспособность системы.

С другой стороны, необходимо, чтобы выбранный критерий отвечал и специфике процессов диагностирования, учитываю­щих вероятностный характер возникновения неисправностей, а в отдельных случаях и экономические издержки диагности­рования (стоимость, ЗИП и т. д.).

Принимая в качестве определяющего параметра точность САУ и используя его в сочетании с вероятностными и экономи­ческими характеристиками системы, можно решить задачу ал­горитмизации поиска дефекта с наибольшей эффективностью.

В простейшем случае оптимизация программы поиска де­фекта сводится к выбору последовательных решений по на­правлению поиска, максимизирующего критерия f(u), в каче­стве которого рассматриваются относительные веса каналов, трактов, блоков, элементов ОД.

В более общем случае задача поиска дефекта сводится к выделению из множества возможных программ программы , которая определит переход из множества начальных со­стояний (каналов) 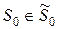во множество конечных состояний (элементов, параметров) так, чтобы критерий f(u) обращался в максимум.

Состояние объекта диагностирования S определяется векто­ром . фазовыми переменными которого (компонен­тами) в момент поиска являются контролируемые параметры, характеризуемые их относительным весом. На каждой стадии n -этапного процесса поиска выбранное (из числа возможных) решение позволяет рассматривать новое состояние системы, ха­рактеризуемое вектором . Причем такой переход со­провождается приростом критерия , зависящим как от прежнего состояния системы S, так и от принятого решения на каждом из шагов (u). Выбор на каждом этапе поиска дефекта осуществляется из конечного числа возможных решений, обусловленных структурой системы и заданными условиями диагно­стирования.

Конечной целью алгоритмизации процесса поиска дефекта является максимизация полного прироста критерия (за N эта­пов принимаемых решений) , зависящего от начального состояния V и числа шагов (этапов) поиска. Используя принцип оптимальности, приходим к основному ре­куррентному соотношению для детерминированной программы поиска:

, () (4.22)

При алгоритмизации процедур поиска дефекта начинают с формулировки обоснованных соображений по определению перечня возможных состояний ОД и набора не­обходимых проверок. Существующие методы определения элементарных и минимальных тестов диагностирования предпола­гают, что такой набор задан и все дефекты равновероятны. Для исследуемых САУ такой подход давал бы неоправданно грубое приближение. Учет весовых коэффициентов каналов, трактов, а в ряде случаев и блоков особенно важен и может быть вы­полнен при определении возможных состояний, приводящих к потере системой работоспособности.

В качестве критерия выбора может быть использован ком­бинированный детерминированно-вероятностный критерий вида

, (4.23)

где – относительный вес контролируемого параметра; р – вероятность дефекта модуля (канала, тракта, блока).

Назовем р* приведенной вероятностью дефекта.

Определяющей в этом случае для перечня рассматриваемых состояний следует считать следующую последовательность: 1) нахождение модуля с максимальным относительным весом параметра u; 2) определение приведенной вероятности модуля ; 3) выбор эквивалентных состояний из условия

Формирование таблицы состояний по указанному принципу позволяет: оправданно включить в нее модули с различной ве­роятностью дефектов (что объективно необходимо) в перечень равновероятных состояний; обоснованно ограничить число рас­сматриваемых состояний, а следовательно, и проверок; учесть специфические требования диагностирования САУ; упростить расчеты по минимизации программ поиска дефекта.

Для подсистем и каналов сложных САУ может быть ис­пользован более совершенный критерий приведения, позволяю­щий учесть допустимые пределы изменений контролируемого параметра из условий аварийных и экстремальных ситуаций. Такой критерий имеет вид

(4.24)

где , 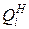– нормированное значение показателя качества модуля; k – число показателей качества модуля; 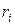– весовой коэффициент показателя качества.

Приведение показателей качества с помощью изложенного выше метода в ряде случаев позволяет существенно упростить задачу. Например, приведение к вероятностям, отвечающим условию

(4.25)

в простейшем случае позволит использовать метод половинного разбиения, эффективный при проверке схем последова­тельно соединенных элементов САУ. Приведение оказывается эффективным и при построении тестов но максимуму информа­ции в предположении неравновероятных дефектов.

Date: 2016-07-18; view: 435; Нарушение авторских прав