Методологические основы технического диагностирования

Одной из наиболее важных характеристик САУ является восстанавливаемость. Контроль работоспособности системы и поиск дефекта, составляющие подчас до 90 % времени, затрачивае­мого на восстановление системы, имеют в этом случае опреде­ляющее значение.

Дальнейшее развитие и усовершенствование САУ приводит к противоречиям. С одной стороны, требования к надежности систем повышаются, с другой — их усложнение приводит, как правило, к снижению надежности. Так как конструктивные, схемные и технологические возможности повышения надеж­ности САУ ограниченны, то очевидным путем устранения этих противоречий является разработка методов и средств контроля работоспособности и поиска дефекта, т. е. решение задач, при­сущих технической диагностике.

Как известно, техническая диагностика направлена на ис­следование текущего состояния объектов диагностирования и форм его проявления во времени, на разработку методов его оп­ределения и принципов построения систем диагностирования.

Технические средства, используемые на различных объектах диагностирования, весьма разнообразны. Поэтому диагностиро­вание должно учитывать различие в формах проявления техни­ческого состояния САУ, целесообразность использования тех или иных методов определения работоспособности и поиска не­исправности и особенности технической реализации средств ди­агностирования.

Условия непрерывной эксплуатации систем различного на­значения в отрыве от ремонтной базы при ограниченном вре­мени их восстановления заставляют ори­ентироваться не только, а подчас и не столько на обнаружение места возникновения дефекта, сколько на определение его ха­рактера, возможных последствий.

Так как рассматриваемыми объектами диагностирования (ОД) являются САУ, то задачи технического диагностирования имеют непосредственную связь с задачами теории управления и с методами, используемыми для их описания и анализа, что и определяет специфику исследований САУ как объекта техни­ческого диагностирования.

Техническое диагностирование предполагает определение технического состояния ОД с определенной точностью. Причем результатом этого процесса должно быть заключение о техни­ческом состоянии объекта с указанием места, а при необходи­мости, вида и причины дефекта.

Поскольку необходимо классифицировать исправное (отсут­ствие дефектов) и неисправное (наличие дефектов) состояние ОД, то возникают задачи формирования математических моде­лей ОД анализа влияния дефектов на работоспособность ОД по тому или иному критерию. Результат такого анализа позволяет определить наиболее рациональный алгоритм поиска неисправ­ности и направление проектирования систем диагностирования. Организация диагностирования может быть представлена схе­мой, приведенной на рис.36.

В процессе функционирования система переходит из одного состояния в другое. В связи с тем, что исходным является ис­правное состояние и оно определено, наиболее существенным следует считать определение оператора перехода системы в те или иные состояния. Математическая формулировка оператора может быть различной в зависимости от природы рассматри­ваемой системы, ее структуры, характера упрощающих предпо­ложений и др. При всех обстоятельствах любое состояние си­стемы должно определяться этим оператором однозначно, в этом состоит его детерминированность.

Ограниченность достоверности знаний закономерности пе­реходов системы приводит в ряде случаев к необходимости ис­пользования вероятностных характеристик.

Переход системы в различные состояния происходит под влиянием возникшей неисправности. При контроле работоспо­собности результат перехода системы в то или иное новое со­ со­стояние известен, хотя не всегда могут быть достоверно опре­делены причины этого перехода. Когда причины неизвестны возможно установить некоторую регулярную взаимосвязанную день событий, которая с определенной достоверностью, зави­сящей от числа и качества наблюдений, устанавливают указан­ную закономерность.

Р и с.36. Организация технического диагностирования САУ

Особенностью детерминированных моделей является един­ственность траекторий, определяющих однозначно связь работо­способности САУ с характером ее неисправности.

Для случайных моделей оператор перехода учитывает вероятностные характеристики. Оператор здесь также имеет детерминированный характер, хотя он и не определяет достоверно траектории перехода системы из одного состояния в другое.

Состояние ОД в общем случае может быть описано n- мерным вектором

, (6.1)

где 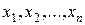- составляющие вектора.

Оператор перехода системы из состояния в состояние может быть описан матрицей вида

, (4.2)

где - коэффициенты преобразования.

Модель дает возможность представить любые процессы в форме линейных и нелинейных преобразований. Например, если вектор Х характеризует исходное состояние системы, то её производное состояние для линейного преобразования вида

(4.3)

может быть записано в виде

(4.4)

Для широкого класса систем, описываемых дифференциальными уравнениями, математическая модель принимает форму

(4.5)

где и 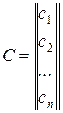- n -мерные векторы,

и - их составляющие.

Вероятностная математическая модель ОД также может быть представлена в векторной форме. Оператор перехода в вы­ражениях (4.4) и (4.5) является при этом матрицей случайных величин.

Принятые принципы представления математических моделей не противоречат методам получения рациональных программ определения работоспособности и поиска дефекта, широко пред­ставленным в различных публикациях. В основе этих методов лежит представление оператора перехода в виде таблицы со­стояний, характеризуемых символами 0 и 1. Использование ука­занного подхода построения математической модели позволяет задать данные состояния, связав их с физически возможными, а следовательно, и правомерными для той или иной системы.

Анализ математической модели ОД должен быть направлен на решение двух основных задач: получение качественной и ко­личественной оценок влияния возможных неисправностей на целевую функцию, характеризующую работоспособность ОД, и определение необходимого и достаточного числа контроли­руемых параметров.

При анализе математических моделей существует две тен­денции. Первая из них состоит в том, что в рассмотрение вво­дится максимально возможное число состояний, в конечном счете определяемое числом элементов САУ. Вторая исходит из того, что второстепенные признаки нецелесообразно принимать во внимание в силу их незначительной информативности.

В случае использования детерминированного оператора (4.2) работоспособность ОД рассматривается в предположении определенного характера изменения параметров САУ.

При учете случайных законов изменения параметров рабо­тоспособность оценивается с помощью вероятностных характе­ристик. Подобное представление модели ОД не противоречит принципам, которые положены в основу построения алгоритмов определения работоспособности САУ и поиска дефекта при представлении процедур диагностики марковскими процессами, поскольку будущее состояние системы действительно может оп­ределяться предыдущим состоянием. В любом случае сущест­вует вероятность того, что система, находящаяся в состоянии j в момент времени t перейдет в состояние i в момент времени t+Δt. Если рассматривать дискретный марковский процесс и характеризовать поведение системы n -мерным вектором с со­ставляющими Р_ij, определяющими вероятность нахождения си­стемы в момент времени t в состоянии j, то поведение системы в момент времени t+1 может быть найдено из решения системы уравнений вида

(4.6)

Направленность на ограничение числа состояний системы вполне оправданна, поскольку учет всех возможных связей, особенно для сложной системы, может создать непреодолимые трудности при разработке модели ОД. Кроме того, степень сложности модели может оказаться слишком высокой и за мно­жеством второстепенных связей могут потеряться основные связи, определяющие процесс функционирования.

Разумное упрощение модели ОД может быть выполнено только при анализе специфики ОД и учете ограничений, дик­туемых задачами диагностирования.

Объективной мерой ограничений служит время, отводимое на восстановление системы, и цена отказа системы. Эти пара­метры взаимосвязаны и образуют единый критерий, характери­зующий эффективность решения задачи или степень возможных последствий, вызванных отказом системы.

Date: 2016-07-18; view: 392; Нарушение авторских прав