Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Скользящее резервирование
|
|
(3.36)
где 
; 
;…; 
; n – число резервных элементов; 
– вероятность безотказной работы одного элемента в течение времени 
; 
; 
– частота отказов одного из основных элементов в момент времени 
, 
При экспоненциальном законе надежности
(3.37)
,
где 
– интенсивность отказов нерезервированной системы; 
–интенсивность отказов элемента; n – число элементов основной системы;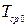 
– среднее время безотказной работы нерезервированной системы; 
– число резервных элементов.
В этом случае кратность резервирования
(3.38)
Приведенные выше формулы [кроме выражений (3.27), (3.30), (3.31)] могут быть использованы только в тех случаях, когда справедливо допущение об отсутствии последействия отказов.
Последействие отказов имеет место практически всегда при постоянном включении резерва, а также в случае резервирования замещением при недогруженном состоянии резерва.
Выражение (3.27) является основным при получении расчетных формул в случае учета влияния последствия отказов. При этом члены 
и 
должны быть записаны с учетом последействия отказав, вида резервирования и его кратности.
Элементы резервированных устройств в ряде случаев могут иметь два вида отказов – «обрыв» и «короткое замыкание». В этом случае вычислять вероятность безотказной работы следует, суммируя вероятности всех благоприятных (не приводящих к отказу) гипотез, т. е.
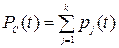, (3.39)
где 
– вероятность j-ой благоприятной гипотезы, вычисленной с учётом двух видов отказов; k – число благоприятных гипотез.
При вычислениях следует иметь в виду, что для элементов сложной системы справедливы выражения
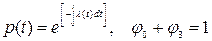(3.40)
где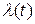 
– интенсивность отказов элемента; 
– вероятность возникновения «обрыва» «короткого замыкания» соответственно.
При экспоненциальном законе надежности
(3.41)
где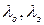 
– интенсивность отказов элемента по «обрыву» и «короткому замыканию» соответственно.
Остальные количественные характеристики надежности в случае необходимости вычисляются через 
по известным аналитическим зависимостям, приведенным ранее.
Date: 2016-07-18; view: 293; Нарушение авторских прав