Теоретические сведения.

ВВЕДЕНИЕ

При решении различных задач, встает вопрос о решении систем нелинейных уравнений. Системы нелинейных уравнений делятся на два вида, а именно, алгебраические и трансцендентные. Без применения численных методов решить можно только малое количество нелинейных систем, лишь частные простые случаи.

В данной курсовой работе реализуется решение нелинейной системы уравнений методом градиентного спуска. Не смотря на то, что сам метод градиентного спуска является методом минимизации функции, существует возможность применения данного метода для систем нелинейных уравнений. Это является весьма полезно и способствует решению многих сложных практических задач.

ПОСТАНОВКА ЗАДАЧИ

Целью данной работы является реализаций метода градиентного спуска для решения систем двух нелинейных уравнений.

При решении поставленной задачи необходимо сравнить полученные данные с данными, полученными стандартными способами решения, чтобы убедиться в правильности реализации метода. Для подбора начального приближения необходимо построить графики функций. Также необходимо вычислить абсолютную и относительную погрешности.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.

Пусть 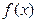– выпуклая функция, определенная на евклидовом пространстве 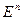, 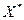– множество минимумов (оно может быть и пустым), 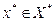– точка минимума; 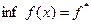; 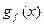– субградиент функции 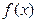в точке .

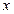Субградиент функции 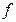в точке есть вектор такой, что

для всех .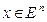

Из определения субградиента следует, что если , то

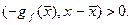(1)

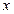Геометрически формула (1) означает, что антисубградиент в точке образует острый угол с произвольным направлением, проведенным из в сторону точки с меньшим значением 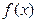. Отсюда, если 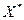непусто, , то при движении из в направлении с достаточно малым шагом расстояние до 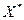убывает. Этот простой факт лежит в основе субградиентного метода или метода обобщенного градиентного спуска (ОГС), впервые предложенного в [1] в связи с решением сетевой транспортной задачи.

Методом обобщенного градиентного спуска (ОГС) называется процедура построения минимизирующей последовательности 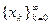, где – начальное приближение, а 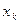строятся по следующей рекуррентной формуле:

(2)

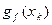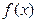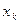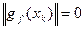здесь – произвольный субградиент функции в точке , – шаговый множитель. Если , то 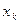– есть точкой минимума функции 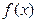и процесс останавливается.

Для использования данного метода в системах уравнений (линейных и нелинейных) требуется свести систему уравнений к одной функции. Представим данные преобразования в общем виде.

Тогда получаем функцию следующего вида

.

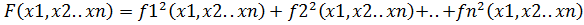Очевидно, что функция 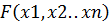примет значение ноль тогда и только тогда, когда каждое слагаемое примет значение ноль. Также очевидно, что такое значение функции 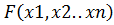будет являться ее минимумом, а также решением системы уравнений.

Следовательно, можно применить методы минимизации для решения систем уравнений, предварительно преобразовав их, как показано выше.

Date: 2016-07-18; view: 251; Нарушение авторских прав