Задачи кинематического анализа

Основной задачей кинематики механизмов является изучение движения звеньев механизмов вне зависимости от сил, действующих на эти звенья. Кинематический анализ состоит из решения трёх задач:

а) определение крайних (мертвых) положений звеньев механизма, перемещения звеньев и траекторий, описываемых точками звеньев;

б) определение скоростей отдельных точек звеньев и угловых скоростей звеньев;

в) определение ускорения отдельных точек звеньев и угловых ускорений звеньев.

Основным назначением механизма является выполнение необходимых движений, которые описываются посредством кинематических характеристик. К ним относятся траектории точек и звеньев, обобщаемые координаты, перемещения точек и звеньев, их скорости и ускорения. По этим характеристикам конструктор выбирает структурную схему механизма и определяет размеры его звеньев.

Звено, которому приписывается одна или несколько обобщенных координат, называют начальным звеном. При плоскопараллельном движении первое звено (начальное), вращающееся вокруг неподвижной оси, т. е. образующее со стойкой вращательную кинематическую пару, имеет одну степень свободы и его положение определяется одним параметром, например: угловой координатой, а звено, перемещающееся поступательно относительно стойки линейной координатой.

Для решения этой задачи должны быть заданы кинематическая схема и функция перемещения начального звена φ = φ(t) − для вращательной пары или S = S(t) – для поступательной.

Кинематическая схема строится в масштабе для ряда положений (8-12 и более) механизма, соответствующим равным углам поворота начального звена за 1 оборот. При этом можно использовать графический либо аналитический способы. После построения кинематической схемы механизма сначала выполняется структурный анализ с целью проверки его на работоспособность, а затем – кинематический анализ.

Рассмотрим графический способ определения положений точек звеньев и точек на примере кривошипно-ползунного механизма (рисунок 2.1)

Рисунок 2.1 − Схема кривошипно-ползунного механизма

Порядок построения положений звеньев механизма можно принять следующим:

1. Наносим на чертеже неподвижные оси О и В, далее радиусом ОА проводим окружность, представляющую собой геометрическое место точек А_.

2. Разбиваем окружность, на несколько равных частей (например, на 8 с точками А₁…А₈), для которых требуется определить положения всех звеньев механизма. Соединив последовательно начальное звено 1 в положениях А₁…А₈ с ползуном 3 посредством звена 2, вычерченного в масштабе, получим положение звеньев в точках 1….8.

3. По найденным положениям звеньев механизма можно построить траектории, описываемые отдельными точками звеньев (например, ползуна или точки С на звене 2), обведя последовательные положения точки, к примеру т. С плавной кривой.

Траектории точек, принадлежащих шатуну, носят названия шатунных кривых. Этими кривыми пользуются в технике для воспроизводства движения рабочих органов различных машин и механизмов.

Масштабы в ТММ.

Значение масштаба рассчитывают по формуле:

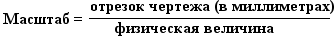
Масштаб длин будет (в миллиметрах на метр); масштаб плана скоростей (в миллиметрах на метр-секунду в минус первой степени), масштаб плана ускорений 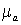(в миллиметрах на метр-секунду в минус второй степени)

Длина отрезка (в миллиметрах), изображающая на схеме начальное звено, берется произвольно. Но целесообразно брать ее кратной реальной длине звена. Размеры остальных звеньев находятся с учетом выбранного масштаба длин.

Кинематическое исследование с помощью планов скоростей и ускорений.

Метод планов скоростей и ускорений относится к графо-аналитическим методам исследования кинематики механизмов.

Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.

Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное - движение данной точки относительно той, движение которой принято за переносное:

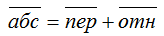
Этот принцип в равной степени относится к перемещениям, скоростям и ускорениям:

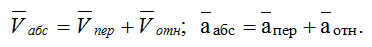
Планы скоростей и ускорений обладают следующими свойствами:

• на плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана. На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает;
• отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек. Вектор относительной скорости направлен на плане к той точке, которая в индексе скорости стоит на первом месте;
• фигуры, образованные точками одного и того же жесткого звена на плане и на механизме, подобны. Поэтому, если на звене известны скорости и ускорения двух точек, то скорость и ускорение любой третьей точки этого же звена можно найти по подобию;
• имея план скоростей, можно найти угловую скорость любого звена механизма. Для определения угловой скорости исследуемого звена надо взять относительную скорость двух любых точек данного звена и разделить на расстояние между этими точками на механизме;
• имея план ускорений, можно найти угловое ускорение любого звена механизма. Для определения углового ускорения исследуемого звена надо взять тангенциальную составляющую относительного ускорения двух любых точек данного звена и разделить на расстояние между этими точками на механизме;
• звенья, соединенные в поступательную кинематическую пару, имеют одинаковые угловые скорости и одинаковые угловые ускорения.

При кинематическом исследовании плоских механизмов методом планов скоростей и ускорений встречается два случая:

1) две точки (одна исследуемая, вторая с известным законом движения, которое принимается в качестве переносного) принадлежат одному и тому же жесткому звену (рисунок 13).

В данном случае относительное движение этих точек получается за счет вращательного движения звена, на котором они находятся. При определении ускорений относительное ускорение раскладывается на нормальное (известное из физики как центростремительное – стремящееся к центру вращения) и тангенциальное.

Рисунок 13

Для примера, приведенного на рисунке 13, нормальное ускорение точки В относительно точки А будет направлено вдоль радиуса ВА к точке А. Тангенциальное – перпендикулярно этому радиусу;

2) звенья соединяются поступательной парой. В этом случае рассматриваются две точки, совпадающие в данный момент времени по своему положению, но принадлежащие разным звеньям – одна ползуну, другая направляющей (рисунок 14).

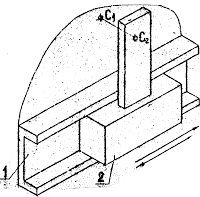
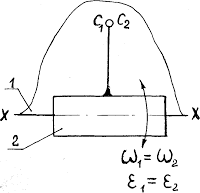
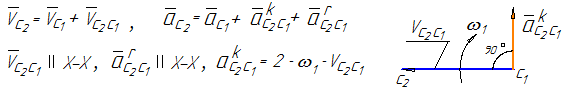
Рисунок 14

Если известен закон движения направляющей 1, то известны характеристики движения любой точки на этом звене, в том числе и точки С₁, принадлежащей этой направляющей.

Движение точки С₁ принимается в качестве переносного. Движение точки С₂, принадлежащей ползуну, относительно точки С₁ получается за счет поступательного движения ползуна вдоль направляющей (влияние вращательного движения исключается, т.к. радиус вращения равен нулю – положение точек С₁ и С₂ совпадает). При определении ускорений кроме относительного ускорения, направленного вдоль направляющей, возникает кориолисово ускорение (см. рисунок 14).

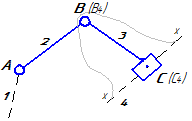
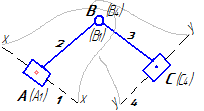
Исследование кинематики механизма методом планов начинается с начального механизма (с входного звена) и далее ведется по группам Ассура в порядке их присоединения к механизму. Для каждой группы Ассура разработаны методы решения (уравнения и порядок построения планов), которые являются неизменными, независимо от того, в каком механизме данная группа Ассура находится. Уравнения планов для групп Ассура второго класса приведены в таблице 3.1.

Таблица 3.1 – Кинематический анализ групп Ассура II класса методом планов

вид группы	конфигурация группы	уравнения для построения планов скоростей и для определения угловых скоростей	уравнения для построения планов ускорений и для определения угловых ускорений

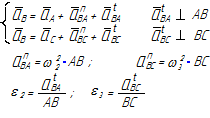
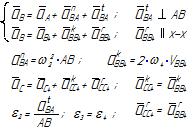
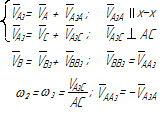
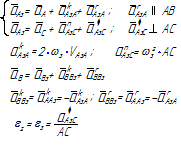
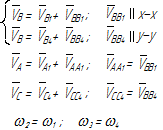
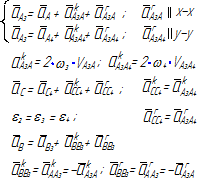
Date: 2016-07-18; view: 671; Нарушение авторских прав