Спирали на Полярном графике

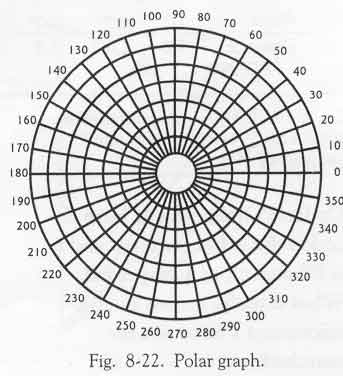Вот как обычно выглядит полярный график (Рис.8-22) с 36-тью радиальными линиями, включая сюда и вертикальную, и горизонтальную линии. Эти линии указывают 360° с десятиградусным возрастанием. Затем, нарисованы концентрические окружности, каждая на одинаковом расстоянии от предыдущей таким образом, вдоль каждого радиуса откладывая восемь равных отрезков, считая внутренний круг как первый. За полярным графиком кроется очень глубокий смысл. Прежде всего подумайте, что он представляет. Это двумерное изображение, где приводится попытка проекцией на плоскую поверхность показать трёхмерную сферу, одну из священных форм. Эта форма – тень. Отбрасываемые тени дают одну из священных возможностей получения информации. К тому же, полярный график составлен из как прямых линий (мужских) так и плавных линий (женских), наложенных друг на друга – мужская и женская энергии единовременно.

П редставьте, что этот маленький центральный круг есть планета в пространстве космоса. С поверхности планеты автор учебника по математике вычертил спираль Золотого Сечения – не Фибоначчи, но Золотого Сечения. Она начинается в нулевом радиусе на поверхности маленькой «планеты» в середине, и описывает один оборот, от нуля до 360 градусов, или назад к нулю (Рис.8-23).

Т еперь, чтобы определить значение каждой точки спирали, вы используете средний круг в качестве единицы (поскольку он представляет расстояние от центра к первой окружности, которую мы назвали «планетой»), и затем отсчитываете единицы наружу до того места, где спираль пересекает радиус. Так, на радиусе в 260° (между четвёртым и пятым кругами) вы отсчитали наружу примерно 4,5. (Конечно, на компьютере вы можете сделать это точнее.) На радиальной линии в 210° спираль достигала почти 3,3. Все ли это поняли?

Т еперь смотрите, что происходит с конкретными значениями от нуля до 360°. При нулевом градусе спираль находится точно на расстоянии одного круга (радиальное возрастание) от центра, поскольку она начинается с поверхности маленькой сферы или планеты. Затем она делает оборот, проходя через различные изменения до тех пор, пока не достигает 120°, где спираль пересекает второй круг. Она продолжает движение наружу к пересечению с четвёртым кругом точно там, где располагается радиальная линия 240°. И восьмого (внешнего) круга она дистигает точно у радиуса 360º (или 0°). Радиальные возрастания удваивались (бинарная последовательность 1,2,4,8) точно в 0°,120°,240° и 360°.

Обратите внимание на Рис.8-24, где показаны точки пересечения спирали. Белые звёздочки слева от столбика радиального возрастания показывают, где бинарная последовательность пересекает радиус. Чёрные звёздочки показывают, как спираль развивается по последовательности Фибоначчи (1,2,3,5,8), пересекая радиусы 120°, 190°, 280° и 360°. Обе последовательности одновременно достигают полного круга (360°), хотя и по различной линии возрастания, следуя этой спирали Золотого Сечения. Эта спираль, показанная на Полярном графике, интегрировала последовательности Фибоначчи и бинарную!

Я был так возбуждён, что несколько дней ходил колесом. Я знал, что обнаружил нечто действительно необычайное, хотя полностью ещё не понимал, что это такое. (Это одна из моих слабых сторон, в которой мне следует тут признаться. Однажды увидев это, я понял, что раз я расшифровал одну из закономерностей, это должно бы быть справедливо и для другой, но я никогда не возвращался к ней, чтобы хотя бы взглянуть на другую модель, которая, вероятно, так же интересна).

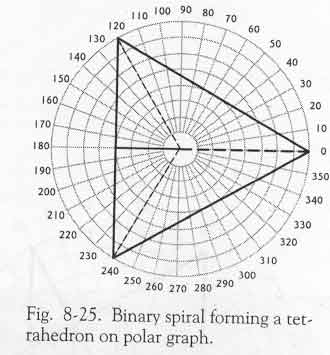
Н о я в самом деле проанализировал, как ведёт себя бинарная последовательность. Спираль пересекается на 0°, 120°, 240° и 360°. Как видите, это даёт образование равнобедренного треугольника (Рис.8-25). Если бы эта бинарная спираль продолжала движение наружу, она пересекала бы радиусы в следующих возрастаниях по градусам 16, 32, 64 и так далее, однако всегда касалась бы этих трёх радиальных линий на 120, 240 и 360 градусах, так как они тоже продолжены.

Т ут есть не только треугольник, но на самом деле вы глядите на трёхмерный тетраэдр, потому что радиусы 120, 240 и 360 градусов продолжаются к центру, образуя как план тетраэдра, так и его вид сбоку.

Н овейшая информация: Была обнаружена ещё одна закономерность, которая, как я и подозревал, оказалась последовательностью Фибоначчи. Однако, я ещё не определил, какова значимость этого открытия для сознания.

Date: 2016-11-17; view: 450; Нарушение авторских прав