Перемещения железобетонных элементов

Прогиб железобетонных элементов, не имеющих тре­щин в растянутых зонах, определяют по жесткости при­веденного сечения В и с учетом значений коэффициента φ при длительном действии нагрузки. Полное значение прогиба

f=f_sh,t+f_lt - f_cp - f_csc,

где f_sh,t - прогиб от кратковременной нагрузки; f_lt - прогиб от по­стоянной и длительно действующих нагрузок; f_cp - выгиб от кратко­временного действия усилия предварительного обжатия Р с учетом всех потерь; f_csc - выгиб вследствие ползучести бетона от обжатия.

Выгиб предварительно напряженных элементов постоянной высоты, вызванный внецентренным обжатием: f_cp=Pe_op/8B

Выгиб предварительно напряженных элементов постоянной высоты, вызванный по­лзучестью бетона от обжатия: f_csc=

Прогиб железобетонных элементов, имеющих трещи­ны в растянутых зонах, определяют по кривизне оси при изгибе: f= (1)

где — изгибающий момент в сечении х от единичной силы, прило­женной по направлению искомого перемещения; 1/r(x) определяют по формуле:

.

При определении перемещений железобетонных элементов постоянного сечения допускается на каждом участке, впределах которого изгибающий момент не меняет знака, вычислять кривизну для наиболее напряженного сечения и далее принимать изменяющейся прямо пропорционально эпюре изгибающих моментов. Это допущение равносильно тому, что жесткость В вычисляют для наиболее напряженного сечения и далее принимают постоянной.

Для предварительно напряженных элементов, к ко­торым предъявляются требования 2-й и 3-й категорий по трещиностойкости, такие допущения в ряде случаев при­водят к существенному завышению прогиба против действительного значения, так как участки с трещинами в растянутой зоне могут иметь ограниченную протяжен­ность. В таких случаях прогиб: 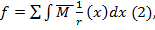при этом эпюру кривизны по длине пролета железобетонного элемента разбивают на несколько участков в виде кусочно-линейной функции и вычисляют интеграл перемещений перемножением эпюр, пользуясь правилом

Верещагина. Кривизну на каждом участке без трещин и с трещинами определяют по формулам

1/r = Мφ/B, .

Углы поворота железобетонных элементов также оп­ределяют интегрированием по (1) или (2), но по моменту в сечении х от единичного момента.

В простейших случаях прогиб изгибаемых элементов без предварительного напряжения - плит, панелей, ба­лок и т. п. - от равномерно распределенной нагрузки

f=(5/384)(ql⁴/B).

Прогиб однопролетных балок и консолей от различ­ных нагрузок определяют по кривизне или по жесткости в сечении с максимальным моментом по общей формуле

F=sl²(1/r) или f=sl²(M/B);

коэффициент s зависит от расчетной схемы элемента и вида нагрузки. Для свободно опертой балки: при равномерно распределенной нагрузке s=5/48, при сосредото­ченном грузе в середине пролета s=1/12, при двух равных моментах по концам s=1/8; для консольной балки: при равномерно распределенной нагрузке s=1/4, при со­средоточенном грузе на свободном конце s=1/3, при моменте на свободном конце s=1/2.

При двузначной эпюре напряжений в неразрезных балках для каждого участка жесткость принимают по­стоянной по сечению с максимальным моментом (рис 1).

Рис.1.Эюры моментов 1 и расчетной Рис.2. Прогиб ж/б элемента при

жесткости 2 двухпролетной балки действии кратковременной и

длительной нагрузок

Прогиб коротких изгибаемых элементов при отноше­нии l/h<10 (подкрановых балок, подстропильных балок и т. п.) должен определяться с учетом влияния попереч­ных сил. В этом случае полный прогиб равен сумме про­гибов, обусловленных деформацией изгиба и деформаци­ей сдвига. Прогиб

,

где 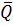- поперечная сила в сечении х от единичной силы, приложен­ной по направлению искомого перемещения; φ— коэффициент, учи­тывающий длительность действия нагрузки; —коэффициент, учи­тывающий влияние трещин на деформацию сдвига и принимаемый на участках по длине элементов, где отсутствуют нормальные и наклон­ные трещины, равным 1; на участках, где только наклонные трещи­ны — 4.8;

=3B/B_crc или - на участках, где только нормальные или нормальные и наклонные трещины; B_crc —жесткость сечення после образования трещин.

Полный прогиб элементов определяют с учетом дли­тельности действий нагрузки по формуле: f=f₁-f₂+f₃-f_crc (3),

где f₁— прогиб от кратковременного действия всей нагрузки; f₂— прогиб от кратковременного действия постоянной и длительной на­грузок; f₃—прогиб от длительного действия постоянной и длитель­ной нагрузок; f_crc — выгиб, вызванный ползучестью бетона от обжатии.

Прогибы f₁ и f₂ вычисляют при значениях ψ_s и λ_b, от­вечающих кратковременному действию нагрузки, а про­гиб f₃— при значениях ψ_s и λ_b, отвечающих длительному действию нагрузки.

Физический смысл формулы (3) можно уяснить из рассмотрения диаграммы зависимости F —f, изобра­женной на рис. 2.

Полный прогиб предварительно напряженных элемен­тов определяют с учетом длительности действия нагруз­ки по полной кривизне:

ВОПРОС №33

Date: 2016-11-17; view: 601; Нарушение авторских прав