
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Общие свойства поперечных электромагнитных волн
|
|
Соотношения (8) и (9) были получены непосредственно из уравнений Максвелла. Они должны выполняться для любых направляемых волн, включая  волны. Полагая в (8) и (9)
волны. Полагая в (8) и (9)  и
и  , приходим к равенствам
, приходим к равенствам  и
и  . Так как
. Так как  и
и  , то эти равенства будут выполняться только при
, то эти равенства будут выполняться только при  . При этом из (12) и (13) следует, что у
. При этом из (12) и (13) следует, что у  волн
волн  и
и  . Следовательно, в тех направляющих системах, в которых возможно распространение
. Следовательно, в тех направляющих системах, в которых возможно распространение  волн, эти волны могут существовать на любой частоте вплоть до
волн, эти волны могут существовать на любой частоте вплоть до 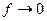 . Поэтому в
. Поэтому в  волны могут распространяться только в тех линиях передачи, в которых может протекать постоянный ток. Этому требованию удовлетворяют направляющие системы, состоящие не менее чем из двух изолированных друг от друга металлических проводников (двухпроводная, коаксиальная, полосковая, экранированная двухпроводная линии и др.). В полых металлических трубах с любой формой поперечного сечения, диэлектрических волноводах и других аналогичных системах распространение
волны могут распространяться только в тех линиях передачи, в которых может протекать постоянный ток. Этому требованию удовлетворяют направляющие системы, состоящие не менее чем из двух изолированных друг от друга металлических проводников (двухпроводная, коаксиальная, полосковая, экранированная двухпроводная линии и др.). В полых металлических трубах с любой формой поперечного сечения, диэлектрических волноводах и других аналогичных системах распространение  волн невозможно. Действительно, предположим, что внутри полой идеально проводящей трубы распространяется ТЕМ-волна. Линии магнитного поля в этом случае должны образовывать замкнутые кривые, лежащие в поперечных плоскостях. Из первого уравнения Максвелла следует, что они должны охватывать продольные линии токов проводимости и(или) смещения. Для существования продольного тока вектор
волн невозможно. Действительно, предположим, что внутри полой идеально проводящей трубы распространяется ТЕМ-волна. Линии магнитного поля в этом случае должны образовывать замкнутые кривые, лежащие в поперечных плоскостях. Из первого уравнения Максвелла следует, что они должны охватывать продольные линии токов проводимости и(или) смещения. Для существования продольного тока вектор  должен иметь продольную составляющую
должен иметь продольную составляющую  . Однако у
. Однако у  волн такой составляющей не может быть по определению.
волн такой составляющей не может быть по определению.
Так как в случае  волн
волн  , то коэффициент фазы, фазовая скорость и длина волны будут совпадать с аналогичными параметрами волны, свободно распространяющейся в безграничной однородной изотропной среде:
, то коэффициент фазы, фазовая скорость и длина волны будут совпадать с аналогичными параметрами волны, свободно распространяющейся в безграничной однородной изотропной среде:
 (27)
(27)
 (28)
(28)
 (29)
(29)
Характеристическое сопротивление  волны легко находится из уравнений (4). Полагая в этих уравнениях
волны легко находится из уравнений (4). Полагая в этих уравнениях  и
и  , приходим к соотношениям, которые можно записать в виде векторного равенства
, приходим к соотношениям, которые можно записать в виде векторного равенства
 (30)
(30)
где
 (31)
(31)
Как видно,  совпадает с характеристическим сопротивлением волны, свободно распространяющейся в безграничной однородной среде с параметрами
совпадает с характеристическим сопротивлением волны, свободно распространяющейся в безграничной однородной среде с параметрами  и
и  .
.
Отметим, что равенства (22), (25) и (30) однотипны и отличаются только значениями характеристических сопротивлений. Эти равенства можно объединить в одну формулу:
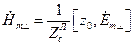 (32)
(32)
где  -характеристическое сопротивление волны, распространяющейся по линии передачи: для
-характеристическое сопротивление волны, распространяющейся по линии передачи: для  волны
волны  , для
, для  волны
волны  и
и  для
для 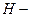 волны.
волны.
Полагая в уравнениях (2)  , сокращая множитель
, сокращая множитель  и учитывая, что в случае
и учитывая, что в случае  волны
волны  и
и  , получаем уравнения для векторов
, получаем уравнения для векторов  и
и  :
:
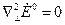 и
и  (33)
(33)
Поле, удовлетворяющее таким уравнениям, является потенциальным. Это означает, что решения уравнений (33) могут быть представлены в виде градиентов от некоторых скалярных функций, например:
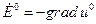 (34)
(34)
где функция  зависит только от поперечных координат и удовлетворяет уравнению Лапласа
зависит только от поперечных координат и удовлетворяет уравнению Лапласа 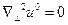 . Аналогичное представление для вектора
. Аналогичное представление для вектора  можно не выписывать, так как векторы
можно не выписывать, так как векторы  и
и  связаны соотношением, аналогичным (9.30):
связаны соотношением, аналогичным (9.30):  .
.
В уравнения (33) не входит частота. Из этого следует, что функции  и
и  , определяющие структуру поля в поперечных сечениях линии, не зависят от частоты и могут быть найдены на основе решения рассматриваемой задачи при
, определяющие структуру поля в поперечных сечениях линии, не зависят от частоты и могут быть найдены на основе решения рассматриваемой задачи при 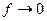 .
.
5. Скорость распространения энергии и групповая скорость
До сих пор рассматривались исключительно монохроматические волны. Однако реальные электромагнитные сигналы являются немонохроматическими: они состоят из конечного либо бесконечного числа монохроматических колебаний с различными частотами. В системах, в которых имеет место дисперсия волн, например линии передачи с использованием  ,
, 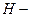 или гибридных волн, диэлектрическая среда с потерями и др., фазовая скорость монохроматической волны зависит от частоты; проходя один и тот же путь, монохроматические волны разной частоты получают разные фазовые сдвиги. В результате изменяется сдвиг по фазе между колебаниями, образующими сигнал. Соответственно изменяется форма сигнала-сигнал искажается. Чем уже спектр сигнала, тем меньше разница между фазовыми скоростями отдельных монохроматических волн, тем очевидно меньше эти искажения.
или гибридных волн, диэлектрическая среда с потерями и др., фазовая скорость монохроматической волны зависит от частоты; проходя один и тот же путь, монохроматические волны разной частоты получают разные фазовые сдвиги. В результате изменяется сдвиг по фазе между колебаниями, образующими сигнал. Соответственно изменяется форма сигнала-сигнал искажается. Чем уже спектр сигнала, тем меньше разница между фазовыми скоростями отдельных монохроматических волн, тем очевидно меньше эти искажения.
Для характеристики перемещения немонохроматических сигналов вводят понятие групповой скорости, обозначая этим термином скорость перемещения максимума огибающей группы монохроматических волн, близких между собой по частоте.
Следовательно, максимум сигнала непрерывно перемещается вдоль оси Z со скоростью
 (35)
(35)
По определению эта величина и является групповой скоростью. Индекс  в (35) опущен, поскольку центральная частота ω0 была выбрана произвольно. При выводе формулы (35) условием применимости 5 явля5ются медленное изменение коэффициента фазы
в (35) опущен, поскольку центральная частота ω0 была выбрана произвольно. При выводе формулы (35) условием применимости 5 явля5ются медленное изменение коэффициента фазы  вблизи частоты
вблизи частоты  и узость спектра сигнала. При невыполнении этих условий влияние дисперсии становится весьма заметным, и сигнал в процессе распространения так сильно меняет свою форму, что само понятие групповой скорости теряет смысл.
и узость спектра сигнала. При невыполнении этих условий влияние дисперсии становится весьма заметным, и сигнал в процессе распространения так сильно меняет свою форму, что само понятие групповой скорости теряет смысл.
В направляющих системах коэффициент фазы описывается выражением (14). Подставляя (14) в (40), находим групповую скорость направляемых волн:
 (36)
(36)
Как видно, при  у
у  ,
, 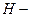 и смешанных волн
и смешанных волн  , а у
, а у  волн
волн 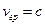
 (37)
(37)
В окрестности максимума сигнала, очевидно, сосредоточена основная часть энергии. Поэтому скорость перемещения максимума сигнала, т.е. групповая скорость, характеризует скорость перемещения энергии электромагнитного поля сигнала по линии передачи. Так как сигнал предполагался узкополосным, то эта скорость должна мало отличаться от скорости распространения энергии v3 монохроматической волны, т.е  . Как показывают расчеты в линиях передачи закрытого типа и некоторых других направляющих системах без потерь
. Как показывают расчеты в линиях передачи закрытого типа и некоторых других направляющих системах без потерь 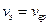 . Поэтому скорость распространения энергии
. Поэтому скорость распространения энергии  в идеальных линиях передачи можно определять по формуле (35) с учетом (37):
в идеальных линиях передачи можно определять по формуле (35) с учетом (37):
 (38)
(38)
Как и следовало ожидать, 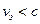 для
для  ,
, 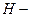 и гибридных волн, и
и гибридных волн, и  для
для  волн. Зависимость
волн. Зависимость  от частоты для
от частоты для  ,
, 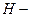 и смешанных волн показана на рис.2. При
и смешанных волн показана на рис.2. При  скорость распространения энергии равна нулю и по мере повышения частоты приближается к скорости света в данной среде.
скорость распространения энергии равна нулю и по мере повышения частоты приближается к скорости света в данной среде.
Date: 2016-11-17; view: 383; Нарушение авторских прав