
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Волновые уравнения для направляемых волн.
|
|
Тема 2
Электромагнитные волны в направляющих системах
Волновые уравнения для направляемых волн.
Рассмотрим произвольную бесконечно протяженную однородную направляющую систему, ориентированную вдоль оси 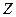 . Будем считать, что направляющая система не вносит потерь.
. Будем считать, что направляющая система не вносит потерь.
В области, где отсутствуют сторонние источники, комплексные амплитуды векторов  и
и  , соответствующие волне, бегущей вдоль однородной линии передачи, могут быть представлены в виде
, соответствующие волне, бегущей вдоль однородной линии передачи, могут быть представлены в виде
 (1)
(1)
где  (коэффициент фазы),
(коэффициент фазы),  и
и  - координаты, изменяющиеся в поперечном сечении рассматриваемой линии передачи. Выбор конкретной системы координат зависит от формы поперечного сечения линии. Множитель
- координаты, изменяющиеся в поперечном сечении рассматриваемой линии передачи. Выбор конкретной системы координат зависит от формы поперечного сечения линии. Множитель 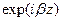 соответствует волне, бегущей в положительном направлении оси
соответствует волне, бегущей в положительном направлении оси 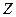 , а множитель
, а множитель 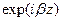 - волне, бегущей в обратном направлении. Для определенности будем считать, что волна распространяется в положительном направлении оси Z.
- волне, бегущей в обратном направлении. Для определенности будем считать, что волна распространяется в положительном направлении оси Z.
Векторы  и
и  должны удовлетворять однородным уравнениям Гельмгольца (. С учетом формул (1) эти уравнения при
должны удовлетворять однородным уравнениям Гельмгольца (. С учетом формул (1) эти уравнения при  и
и  могут быть переписаны в виде
могут быть переписаны в виде
 (2)
(2)
где
 (3)
(3)
а оператор  . Величину
. Величину  называют поперечным волновым числом.
называют поперечным волновым числом.
Покажем, что в тех случаях, когда векторы  и
и  (оба или один из них) имеют продольные составляющие, нахождение поля направляемой волны может быть сведено к определению составляющих
(оба или один из них) имеют продольные составляющие, нахождение поля направляемой волны может быть сведено к определению составляющих  и
и  , так как поперечные составляющие векторов поля выражаются через продольные. Проецируя уравнения Максвелла на оси
, так как поперечные составляющие векторов поля выражаются через продольные. Проецируя уравнения Максвелла на оси  и
и  декартовой системы координат и учитывая, что в рассматриваемом случае дифференцирование по переменной
декартовой системы координат и учитывая, что в рассматриваемом случае дифференцирование по переменной  эквивалентно умножению на
эквивалентно умножению на  , получаем
, получаем

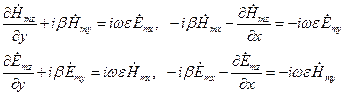 (4)
(4)
Система уравнений (4) позволяет выразить составляющие  ,
,  ,
,  и
и 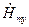 через
через
 и
и  . После элементарных преобразований имеем
. После элементарных преобразований имеем

 (5)
(5)
Система уравнений (5) связывает поперечные и продольные составляющие векторов поля в декартовой системе координат. Для выражения этой связи в произвольной системе координат перейдем к векторной форме уравнений (5). Введем векторы
 (6)
(6)
 , (7)
, (7)
связанные с  и
и  соотношением
соотношением  и
и  . Подставляя а (6) вместо
. Подставляя а (6) вместо  и
и  их выражения из (5), приходим к равенству
их выражения из (5), приходим к равенству
 ,
,
которое может быть переписано в виде
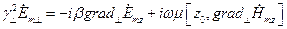 , (8)
, (8)
где оператор  .
.
Аналогично доказывается равенство
 (9)
(9)
Продольные составляющие  и
и  удовлетворяют уравнениям
удовлетворяют уравнениям
 (10)
(10)
вытекающим из (2).
Таким образом, для определения поля  и гибридных волн достаточно найти составляющие
и гибридных волн достаточно найти составляющие  и
и  путем решения уравнений (10) с учетом краевых условий, соответствующих рассматриваемой направляющей системе, а для вычисления поперечных составляющих использовать равенства (5) или (8) и (9).
путем решения уравнений (10) с учетом краевых условий, соответствующих рассматриваемой направляющей системе, а для вычисления поперечных составляющих использовать равенства (5) или (8) и (9).
У ТЕМ-волн продольные составляющие векторов  и
и  отсутствуют (
отсутствуют ( и
и  ).
).
2. Общие свойства и параметры электрических, магнитных и гибридных волн
В случае электрических ( и
и  ), магнитных (
), магнитных (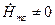 ,
,  ) и гибридных (
) и гибридных (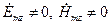 ) волн постоянная
) волн постоянная  отлична от нуля. Это следует, в частности, из равенств (8) и (9). Для каждой конкретной линии передачи она может быть определена в результате решения уравнений (10) и учета краевых условий, соответствующих этой линии. Постоянная
отлична от нуля. Это следует, в частности, из равенств (8) и (9). Для каждой конкретной линии передачи она может быть определена в результате решения уравнений (10) и учета краевых условий, соответствующих этой линии. Постоянная  зависит от формы и размеров поперечного сечения линии передачи и от типа распространяющейся волны, но не зависит от частоты.
зависит от формы и размеров поперечного сечения линии передачи и от типа распространяющейся волны, но не зависит от частоты.
Выражая коэффициент фазы р из (3), получаем
 (11)
(11)
Так как  , то в зависимости от частоты подкоренное выражение в (11) может быть положительным (при
, то в зависимости от частоты подкоренное выражение в (11) может быть положительным (при  ), равным нулю (при
), равным нулю (при  .) или отрицательным (при
.) или отрицательным (при  ).
).
В первом случае параметр  - действительное число и фазы составляющих векторов поля в фиксированный момент
- действительное число и фазы составляющих векторов поля в фиксированный момент  линейно зависят от координаты
линейно зависят от координаты  , что является признаком распространения волны вдоль оси
, что является признаком распространения волны вдоль оси 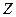 с постоянной скоростью
с постоянной скоростью  . Как будет видно из дальнейшего, распространение волны в этом случае сопровождается переносом энергии вдоль оси
. Как будет видно из дальнейшего, распространение волны в этом случае сопровождается переносом энергии вдоль оси 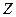 .
.
В третьем случае  . Подкоренное выражение в (11) оказывается отрицательным, и
. Подкоренное выражение в (11) оказывается отрицательным, и  . Знак в правой части последнего равенства выбран из физических соображений: при этом множитель
. Знак в правой части последнего равенства выбран из физических соображений: при этом множитель  и амплитуды составляющих векторов
и амплитуды составляющих векторов  и
и  экспоненциально убывают вдоль оси
экспоненциально убывают вдоль оси 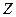 . Если принять
. Если принять  , то амплитуды векторов поля будут возрастать с удалением от источников, что в рассматриваемой задаче физически невозможно. Фазы составляющих векторов поля в данном случае не зависят от координат: поле имеет характер стоячей волны и экспоненциально уменьшается вдоль оси
, то амплитуды векторов поля будут возрастать с удалением от источников, что в рассматриваемой задаче физически невозможно. Фазы составляющих векторов поля в данном случае не зависят от координат: поле имеет характер стоячей волны и экспоненциально уменьшается вдоль оси 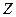 . Переноса энергии вдоль линии передачи в этом случае не происходит. Подчеркнем, что экспоненциальное убывание поля вдоль линии передачи не связано с потерями энергии: рассматривается идеальная направляющая система, в которой потери отсутствуют.
. Переноса энергии вдоль линии передачи в этом случае не происходит. Подчеркнем, что экспоненциальное убывание поля вдоль линии передачи не связано с потерями энергии: рассматривается идеальная направляющая система, в которой потери отсутствуют.
Во втором случае параметр  . Такой режим называют критическим. Частота
. Такой режим называют критическим. Частота  , определяемая из условия
, определяемая из условия  , называется критической частотой:
, называется критической частотой:
 (12)
(12)
Соответствующая этой частоте критическая длина волны
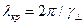 (13)
(13)
Выражая  из (13) и подставляя в (11), получаем
из (13) и подставляя в (11), получаем
 (14)
(14)
Как видно, параметр β является действительной величиной, т.е. поле (1) представляет собой распространяющуюся волну, только при выполнении условия
 (15)
(15)
Неравенство (15) можно переписать в виде
 (16)
(16)
Таким образом,  ,
, 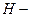 и гибридные волны в идеальной линии передачи могут распространяться только на частотах, превышающих некоторую критическую частоту, определяемую формулой (12). Отметим, что значение
и гибридные волны в идеальной линии передачи могут распространяться только на частотах, превышающих некоторую критическую частоту, определяемую формулой (12). Отметим, что значение  зависит от формы и размеров поперечного сечения линии и типа волны.
зависит от формы и размеров поперечного сечения линии и типа волны.
Неравенство (15), а также (16) называют условием распространения волны в линии передачи.
По аналогии с обычным определением назовем длиной направляемой волны  , распространяющейся в линии передачи, расстояние между двумя поперечными сечениями, в которых в один и тот же момент времени фазы составляющих вектора
, распространяющейся в линии передачи, расстояние между двумя поперечными сечениями, в которых в один и тот же момент времени фазы составляющих вектора  (или
(или  ) отличаются на
) отличаются на  . Очевидно также, что длина волны
. Очевидно также, что длина волны  равна расстоянию, на которое поверхность равной фазы перемещается за период. Так как зависимость всех составляющих векторов поля от координаты
равна расстоянию, на которое поверхность равной фазы перемещается за период. Так как зависимость всех составляющих векторов поля от координаты  определяется множителем
определяется множителем  , то
, то
 (17)
(17)
а фазовая скорость вычисляется по формуле
 (18)
(18)
|
 Как видно, при
Как видно, при  длина волны в линии и фазовая скорость
длина волны в линии и фазовая скорость  и гибридных волн больше соответственно длины волны
и гибридных волн больше соответственно длины волны  и фазовой скорости
и фазовой скорости  волны, свободно распространяющейся в безграничной однородной среде без потерь с параметрами
волны, свободно распространяющейся в безграничной однородной среде без потерь с параметрами  и
и  . Отметим, что у
. Отметим, что у  и гибридных волн фазовая скорость зависит от частоты. Это явление называют дисперсией волн. При
и гибридных волн фазовая скорость зависит от частоты. Это явление называют дисперсией волн. При  фазовая скорость равна бесконечности, при увеличении частоты
фазовая скорость равна бесконечности, при увеличении частоты 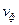 приближается к скорости света (рис.2).
приближается к скорости света (рис.2).
Общие выражения для критической длины волны (13), критической частоты (12), коэффициента фазы (14), длины волны в линии (17) и фазовой скорости (18) одинаковы для  и гибридных волн. Однако из этого не следует, что значения перечисленных параметров будут одинаковыми для этих волн. Критическая длина волны зависит от поперечного волнового числа (
и гибридных волн. Однако из этого не следует, что значения перечисленных параметров будут одинаковыми для этих волн. Критическая длина волны зависит от поперечного волнового числа (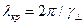 ). В свою очередь, значение
). В свою очередь, значение  зависит от формы и размеров поперечного сечения линии передачи и от структуры поля распространяющейся волны. Структура поля
зависит от формы и размеров поперечного сечения линии передачи и от структуры поля распространяющейся волны. Структура поля  и гибридных волн различна, поэтому в общем случае соответствующие данным волнам значения
и гибридных волн различна, поэтому в общем случае соответствующие данным волнам значения  могут не совпадать. При этом для указанных волн не будут совпадать и значения параметров
могут не совпадать. При этом для указанных волн не будут совпадать и значения параметров  .
.
Перейдем к вычислению характеристических сопротивлений рассматриваемых волн. По определению характеристическое сопротивление волны равно отношению поперечных к направлению распространения составляющих векторов  и
и  .
.
В случае  волн поперечные составляющие векторов
волн поперечные составляющие векторов  и
и  определяются формулами
определяются формулами
 (19)
(19)
 (20)
(20)
получающимися из (8) и (9) при  . Подставляя в (20) выражение для
. Подставляя в (20) выражение для 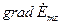 из (19), приходим к соотношению
из (19), приходим к соотношению  . Аналогичное равенство выполняется и для векторов
. Аналогичное равенство выполняется и для векторов  и
и  , где
, где  и
и  - продольные составляющие векторов
- продольные составляющие векторов  и
и  , введенных формулами (1). Как видно, векторы
, введенных формулами (1). Как видно, векторы  и
и  (а также
(а также  и
и  ) взаимно перпендикулярны. Из полученного соотношения вытекает следующее выражение для характеристического сопротивления
) взаимно перпендикулярны. Из полученного соотношения вытекает следующее выражение для характеристического сопротивления  волн:
волн:
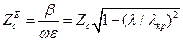 (21)
(21)
где  . При этом соотношение, связывающее поперечные составляющие векторов
. При этом соотношение, связывающее поперечные составляющие векторов  и
и  в случае
в случае  волн принимает вид
волн принимает вид
 (22)
(22)
Характеристическое сопротивление  волн зависит от длины волны (от частоты). При
волн зависит от длины волны (от частоты). При  оно всегда меньше
оно всегда меньше  . На критической частоте (при
. На критической частоте (при  )
)  . При уменьшении
. При уменьшении 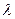 (т.е. при увеличении частоты от
(т.е. при увеличении частоты от  до бесконечности)
до бесконечности)  возрастает от нуля до
возрастает от нуля до  (рис. 3).
(рис. 3).
Аналогично вычисляется характеристическое сопротивление  волн
волн  . Полагая в (8) и (9)
. Полагая в (8) и (9) 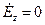 , получаем
, получаем
 (23)
(23)
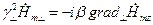 (24)
(24)
Подставляя выражение для  из (24) в (23), приходим к равенству
из (24) в (23), приходим к равенству  . Умножая векторно обе части этого равенства на орт
. Умножая векторно обе части этого равенства на орт  и раскрывая двойное векторное произведение по формуле (П.31), получаем
и раскрывая двойное векторное произведение по формуле (П.31), получаем
 (25)
(25)
где
 (26)
(26)
 Как видно, в случае
Как видно, в случае 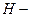 волн векторы
волн векторы  и
и  (и соответствующие им векторы
(и соответствующие им векторы  и
и  ) как и аналогичные им векторы в случае
) как и аналогичные им векторы в случае  волн, взаимно перпендикулярны. Характеристическое сопротивление
волн, взаимно перпендикулярны. Характеристическое сопротивление 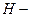 волн зависит от частоты. При
волн зависит от частоты. При  оно всегда больше
оно всегда больше  . При увеличении частоты от критической до бесконечности
. При увеличении частоты от критической до бесконечности  убывает от бесконечности до
убывает от бесконечности до  (см.рис.3).
(см.рис.3).
|
 ) характеристические сопротивления
) характеристические сопротивления  и
и 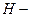 волн являются чисто мнимыми величинами. Это означает что при
волн являются чисто мнимыми величинами. Это означает что при  поперечные составляющие векторов напряженностей электрического и магнитного полей
поперечные составляющие векторов напряженностей электрического и магнитного полей  и
и  на 90°. Очевидно, что при этом комплексный вектор Пойнтинга принимает чисто мнимые значения, т.е. вдоль линии не происходит переноса энергии. Поле в линии при
на 90°. Очевидно, что при этом комплексный вектор Пойнтинга принимает чисто мнимые значения, т.е. вдоль линии не происходит переноса энергии. Поле в линии при  являвется чисто реактивным. Напомним, что все формулы данного раздела получены в предположении, что линия является идеальной (не вносит потерь).
являвется чисто реактивным. Напомним, что все формулы данного раздела получены в предположении, что линия является идеальной (не вносит потерь).
В случае гибридных потерь ( ) поперечные составляющие векторов
) поперечные составляющие векторов  и
и  определяются общими формулами (8) и (9). Поэтому получить единое простое выражение для характеристического сопротивления не удается: его величина зависит и от линии передачи, и от структуры поля распространяющейся волны и при
определяются общими формулами (8) и (9). Поэтому получить единое простое выражение для характеристического сопротивления не удается: его величина зависит и от линии передачи, и от структуры поля распространяющейся волны и при  может быть как больше, так и меньше
может быть как больше, так и меньше  . На частотах, меньших критической (
. На частотах, меньших критической ( ), характеристическое сопротивление гибридных волн также принимает чисто мнимые значения.
), характеристическое сопротивление гибридных волн также принимает чисто мнимые значения.
Date: 2016-11-17; view: 440; Нарушение авторских прав