Нестационарное электромагнитное поле

1. Запишите основной закон электромагнитной индукции в интегральной форме. Фарадеем для нестационарных полей был установлен закон, получивший название закон электромагнитной индукции. Суть этого закона состоит в следующем: изменение потока вектора магнитной индукции через замкнутый контур приводит к возникновению в этом контуре электродвижущей силы. Закон электромагнитной индукции (закон Фарадея-Максвелла): ЭДС электромагнитной индукции в контуре пропорциональна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, натянутую на этот контур, т.е. . В интегральной форме (эквивалентной) закон Фарадея можно записать в следующем виде: Здесь — напряжённость электрического поля, 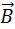— магнитная индукция, S — произвольная поверхность, L — её граница. Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).

2. В чем состоит явление самоиндукции. Самоиндукцией называется возникновение ЭДСэлектромагнитной индукции в электрической цепи вследствиеизменения в ней электрического тока. Эта ЭДС называется электродвижущей силой самоиндукции (). Явление самоиндукции состоит в том, что при изменении силы тока в контуре возникает ЭДС индукции в этом же самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре.

3. В чем состоит явление взаимной индукции. Взаимной индукцией называется явление возбуждения ЭДС электромагнитной индукции в одной электрической цепи при изменении электрического тока в другой цепи или при изменении взаимного расположения этих двух цепей. Эта ЭДС называется электродвижущей силой взаимной индукции (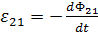). Явление взаимоиндукции наблюдается между близко расположенными катушками. Сущность взаимоиндукции заключается в переносе электрической энергии из одной цепи в другую посредством общего магнитного поля: в одном из контуров электрическая энергия преобразуется в энергию магнитного поля, в другом контуре происходит обратный переход энергии магнитного поля в электрическую энергию. Из сказанного следует, что магнитное поле является переносчиком электрической энергии из одной цепи в другую.

4. Запишите выражение для магнитной энергии тока. Работа идет на приращение внутренней энергии сопротивления R, соленоида и соединительных проводов (т.е. на их нагревание). Совершение этой работы сопровождается исчезновением магнитного поля, которое первоначально существовало в окружающем соленоид пространстве. Поскольку никаких других изменений в окружающих электрическую цепь телах не происходит, остается заключить, что магнитное поле является носителем энергии, за счет которой и совершается работа. Таким образом, мы приходим к выводу, что проводник с индуктивностью L, по которому течет ток силы I, обладает энергией , которая локализована в возбуждаемом током магнитном поле.

5. Запишите выражение для плотности энергии магнитного поля через вектора, характеризующие электромагнитное поле. Магнитное поле бесконечно длинного соленоида однородно и отлично от нуля только внутри соленоида. Следовательно, энергия локализована внутри соленоида и распределена по его объему с постоянной плотностью , которую можно найти, разделив W на V. Произведя это деление, получим . Воспользовавшись соотношением H , формуле для плотности энергии магнитного поля можно придать вид . Здесь B и H – модули векторов магнитной индукции и напряженности в рассматриваемой точке магнитного поля.

6. Запишите первое уравнение Максвелла в интегральной форме и дайте соответствующую формулировку. Первое уравнение Максвелла является обобщением электромагнитной индукции . Анализируя явление электромагнитной индукции, Максвелл пришел к его углубленному истолкованию, заключающемуся в том, что всякое изменение магнитного тока возникает появление вихревого электрического поля и, таким образом, пришел к выражению: (циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром). Физический смысл: переменное магнитное поле порождает вокруг себя вихревое электрическое поле.

7. Запишите второе уравнение Максвелла в интегральной форме и дайте соответствующую формулировку. Второе уравнение Максвелла является обобщением, так называемого, закона полного тока. Максвелл дал обобщенную формулировку закона полного тока, введя понятие тока смещения . Следует отметить, что ток проводи-мости и ток смещения в вакууме имеют различную физическую сущность. Ток смещения не сопровождается выделением тепла. С учетом тока смещения , где ), тогда (Циркуляция вектора напряженности магнитного поля по произвольного замкнутого контура прямо пропорциональна суммарному току, пересекающему поверхность, охватываемую этим контуром). Физический смысл: магнитное поле создаётся не только токами проводимости, но и изменяющимся во времени электрическим полем.

8. Из каких элементов состоит идеальный колебательный контур. Простейшая система, в которой могут происходить свободные электромагнитные колебания, состоит из конденсатора и катушки, присоединенной к его обкладкам. Такая система называется колебательным контуром. Колебательный контур – это электрическая цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R.

9. Запишите зависимость величины заряда на обкладках конденсатора идеального колебательного контура (его активное сопротивление равно нулю) от времени. Уравнение колебаний в контуре без активного сопротивления имеет вид . Решением этого дифференциального уравнения является функция q (t), то есть уравнение свободных незатухающих гармонических колебаний величины заряда q на обкладках конденсатора: , где – величина заряда на обкладках конденсатора в момент времени t; – амплитуда колебаний заряда на обкладках конденсатора; – круговая (или циклическая) частота колебаний (); – фаза колебаний в момент времени t; – начальная фаза колебаний, то есть фаза колебаний в момент времени t =0.

10. Запишите зависимость величины заряда на обкладках конденсатора колебательного контура от времени при затухающих колебаниях. Всякий реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, расходуется в этом сопротивлении на нагревание, вследствие чего свободные колебания затухают. Уравнение в этом случае имеет вид 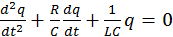. Решением этого дифференциального уравнения является функция q (t), то есть уравнение свободных затухающих гармонических колебаний величины заряда q на обкладках конденсатора: , где – величина заряда на обкладках конденсатора в момент времени t; - амплитуда затухающих колебаний заряда на обкладках конденсатора в момент времени t; - начальная амплитуда затухающих колебаний заряда на обкладках конденсатора; – круговая (или циклическая) частота колебаний ; – фаза колебаний в момент времени t; – начальная фаза колебаний, то есть фаза колебаний в момент времени t =0.

Запишите выражение (через энергию) для добротности контура.Колебательный контур часто характеризуется его добротностью Q, которая определяется как величина, обратно пропорциональная логарифмическому декременту затухания:. Из этой формулы следует, что добротность контура тем выше, чем большее число колебаний усевает совершиться прежде, чем амплитуда уменьшится в e раз. В случае слабого затухания.

12. Как изменяется амплитуда затухающих свободных колебаний со временем. Затухающие колебания не являются периодическими. Например, максимальное значение колеблющейся величины s, достигаемое в некоторый момент времени , в последующем (при ) никогда не повторяется. Однако при затухающих колебаниях величина s обращается в нуль, изменяясь в одну и ту же сторону (например, убывая), а также достигает максимальных и минимальных значений через равные промежутки времени: . Поэтому величины и условно называют периодом (условным периодом) и циклической частотой (условной циклической частотой) затухающих колебаний. Величина называется амплитудой затухающих колебаний, соответственно – начальная амплитуда. Амплитуда затухающих колебаний уменьшается с течением времени и тем быстрее, чем больше коэффициент затухания β. Промежуток времени , в течение которого амплитуда затухающих колебаний уменьшается в e раз, называется временем релаксации.

13. Запишите формулу Томсона.Формула Томсона названа в честь английского физика Уильяма Томсона, который вывел её в 1853 году, и связывает период собственных электрических колебаний в контуре с его ёмкостью и индуктивностью. Формула Томсона выглядит следующим образом: .

14. Чему равно полное сопротивление цепи переменному электрическому току, если она содержит активное сопротивление, катушку индуктивности и конденсатор. Выражение называется полным электрическим сопротивлением или импедансом. Омическое сопротивление R цепи называют также активным, оно обусловливает выделение теплоты в цепи в соответствии с законом Джоуля—Ленца. Разность индуктивного и емкостного сопротивлений (X_L – Х_С) называют реактивным сопротивлением. Оно не вызывает нагревания элементов электрической цепи.

15. Поток вектора магнитной индукции (формулировка, математическая запись), размерность. Потоком вектора магнитной индукции называется скалярная физическая величина , равная скалярному произведению вектора на вектор площади . Поток магнитной индукции может быть положительным и отрицательным в зависимости от знака 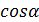. Магнитный поток измеряется в веберах Тл·м² = Вб (Вебер). 1 Вебер – это магнитный поток, создаваемый магнитным полем с индукцией в 1 Тл через площадь 1 м². В случае неоднородного поля рассматривается элементарный поток через элементарную площадь dS. d Ф _B = 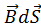Тогда суммарный магнитный поток будет равен интегралу по площади S .

16. Запишите выражение для емкостного сопротивления цепи. Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т. е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты. Для постоянного тока, т. е. когда частота его равна нулю, сопротивление емкости бесконечно велико; поэтому постоянный ток по цепи с емкостью проходить не может. Величина емкостного сопротивления (реактивного емкостного сопротивления) определяется по следующей формуле: , где Хс — емкостное сопротивление конденсатора в Ом; ω — угловая частота переменного тока; С — емкость конденсатора в Ф.

17. Запишите выражение для индуктивного сопротивления цепи. Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением. Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю. Подсчет индуктивного сопротивления катушки для переменного тока производится по формуле , где X_L — индуктивное сопротивление в Ом; ω — угловая частота переменного тока; L — индуктивность катушки в Гн. Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.

Date: 2016-11-17; view: 703; Нарушение авторских прав