
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Стационарное электромагнитное поле
|
|
ЭЛЕКТРОСТАТИКА
1. Сформулируйте и запишите в векторной форме закон Кулона. Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с соединяющей заряды прямой. Закон Кулона в векторной форме представляется формулой: F  . В скалярной форме:
. В скалярной форме:  , где k – коэффициент пропорциональности,
, где k – коэффициент пропорциональности,  – величины взаимодействующих зарядов,
– величины взаимодействующих зарядов,  единичный вектор, имеющий направление от заряда
единичный вектор, имеющий направление от заряда  ,
,  – расстояние между зарядами,
– расстояние между зарядами, 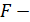 сила, действующая на заряд
сила, действующая на заряд  .
.
2. Запишите выражение для потенциала электростатического поля, созданного точечным зарядом в точке, находящейся от него на расстоянии r. Для работы по перемещению заряда в электрическом поле, создаваемом подвижным точечным зарядом, потенциал электрического поля точечного заряда равен: 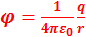 .В гауссовой системе потенциал поля точечного заряда в вакууме определяется формулой
.В гауссовой системе потенциал поля точечного заряда в вакууме определяется формулой  .
.
3. Запишите выражение для напряженности электростатического поля, созданного точечным зарядом в точке, находящейся от него на расстоянии r. Напряженность электростатического поля в вакууме точечного заряда q можно найти из закона Кулона:  , где
, где  – радиус-вектор, соединяющий заряд q с точкой, где вычисляется напряженность поля. Направлен вектор E вдоль радиальной прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен.
– радиус-вектор, соединяющий заряд q с точкой, где вычисляется напряженность поля. Направлен вектор E вдоль радиальной прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен.
4. Что является силовой характеристикой электростатического поля. Назовите единицу ее измерения в СИ. Основной количественной характеристикой электрического поля служит вектор Е напряженности электрического поля, являющийся его силовой характеристикой. Он равен отношению силы F, которая действует со стороны электрического поля на точечный пробный заряд, помещенный в рассматриваемую точку поля, к величине q этого заряда  . Если известна силовая характеристика эл. поля, то можно найти силу (и по величине и по направлению) действующую на любой заряд в любой точке поля. В СИ единица напряженности электрического поля имеет название вольт на метр и обозначается В/м. (Е, вектор)
. Если известна силовая характеристика эл. поля, то можно найти силу (и по величине и по направлению) действующую на любой заряд в любой точке поля. В СИ единица напряженности электрического поля имеет название вольт на метр и обозначается В/м. (Е, вектор)
5. Что является энергетической характеристикой электростатического поля. Назовите единицу ее измерения в СИ. Энергетической характеристикой электростатического поля служит его потенциал. Потенциалом электростатического поля называется физическая величина  , равная отношению потенциальной энергии
, равная отношению потенциальной энергии 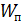 пробного точечного электрического заряда, помещенного в рассматриваемую точку поля, к величине q этого заряда:
пробного точечного электрического заряда, помещенного в рассматриваемую точку поля, к величине q этого заряда:  . Если известна энергетическая характеристика эл. поля, то можно найти энергию которую приобретает любой заряд внесенный в любую точку поля по отношению к избранному заранее нулевому значению (чаще всего нулевое значение энергии приписывают бесконечно удаленной точке). В СИ единицей измерения потенциала электростатического поля является 1 Вольт. (
. Если известна энергетическая характеристика эл. поля, то можно найти энергию которую приобретает любой заряд внесенный в любую точку поля по отношению к избранному заранее нулевому значению (чаще всего нулевое значение энергии приписывают бесконечно удаленной точке). В СИ единицей измерения потенциала электростатического поля является 1 Вольт. ( , скаляр)
, скаляр)
6. Как проводятся силовые линии электростатического поля. Имеют ли они начало и конец. Если да – то где они начинаются и заканчиваются. Силовые линии (линии напряженности) проводят таким образом, чтобы касательная к ним в каждой точке совпадала с направлением вектора напряженности поля в этой точке. Силовые линии считаются направленными так же, как вектор напряженности. Они нигде не пересекаются, так как в каждой точке поля вектора напряженности имеет лишь одно направление (в сторону уменьшения потенциала). Силовые линии нигде, кроме заряда, не начинаются и не заканчиваются. Они начинаются на положительном заряде и заканчиваются на отрицательном заряде. В случае одного положительного заряда силовые линии начинаются на положительном заряде и уходят на бесконечность, а в случае одного отрицательного заряда силовые линии приходят из бесконечности и сходятся на отрицательном заряде. Это свойство линий напряженности является общим для всех электростатических полей: линии напряженности могут начинаться или заканчиваться лишь на зарядах либо уходить в бесконечность.
7. Что называется электрическим диполем. Записать формулу дипольного момента. Электрическим диполем называется система двух одинаковых по величине разноименных точечных зарядов +q и –q, расстояние l между которыми значительно меньше расстояния до тех точек, в которых определяется поле системы. Прямая, проходящая через оба заряда, называется осью диполя. Электрический момент диполя определяется по формуле:  , где
, где  – плечо диполя. Вектор
– плечо диполя. Вектор  направлен по оси диполя от отрицательного заряда к положительному.
направлен по оси диполя от отрицательного заряда к положительному.
8. Что называется потоком вектора напряженности электростатического поля (  ) через площадку dS. Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности Ф через эту поверхность. Элементарным потоком напряженности электрического поля сквозь малый участок площадью dS поверхности, проведенной в поле, называется величина: d Ф =EdScos
) через площадку dS. Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности Ф через эту поверхность. Элементарным потоком напряженности электрического поля сквозь малый участок площадью dS поверхности, проведенной в поле, называется величина: d Ф =EdScos  , где
, где  – угол между вектором
– угол между вектором  и единичным вектором нормали к площадке dS. Это выражение можно записать в другом виде: d Ф =
и единичным вектором нормали к площадке dS. Это выражение можно записать в другом виде: d Ф =  , где
, где  – проекция вектора
– проекция вектора  на нормаль к площадке dS. Если поверхность S не бесконечно мала, то при вычислении потока вектора напряженности
на нормаль к площадке dS. Если поверхность S не бесконечно мала, то при вычислении потока вектора напряженности  через поверхность S эту поверхность надо условно разбить на бесконечно малые площадки dS, а затем вычислить интеграл по всей поверхности S:
через поверхность S эту поверхность надо условно разбить на бесконечно малые площадки dS, а затем вычислить интеграл по всей поверхности S:  .
.
9. Запишите выражение для потенциальной энергии взаимодействия двух точечных зарядов. Пусть два точечных заряда q1 и q2 находятся в вакууме на расстоянии r друг от друга. Можно показать, что потенциальная энергия их взаимодействия даётся формулой:  . Это энергия взаимодействия двух точечных зарядов, которая в зависимости от знака зарядов, может быть как положительной, так и отрицательной. Можно говорить, что заряд q2 в поле, созданном зарядом q1 обладает потенциальной энергией Wp.
. Это энергия взаимодействия двух точечных зарядов, которая в зависимости от знака зарядов, может быть как положительной, так и отрицательной. Можно говорить, что заряд q2 в поле, созданном зарядом q1 обладает потенциальной энергией Wp.
10. Какую работу надо совершить, чтобы переместить заряд q из точки с потенциалом 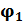 в точку с потенциалом
в точку с потенциалом  . Работа сил поля над зарядом q может быть выражена через разность потенциалов:
. Работа сил поля над зарядом q может быть выражена через разность потенциалов:  . Таким образом, работа, совершаемая над зарядом силами поля, равна произведению величины заряда на разность потенциалов в начальной и конечной точках (т.е. на убыль потенциала).
. Таким образом, работа, совершаемая над зарядом силами поля, равна произведению величины заряда на разность потенциалов в начальной и конечной точках (т.е. на убыль потенциала).
11. Запишите выражение для напряженности электростатического поля, созданного равномерно заряженной с поверхностью зарядов 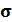 бесконечной плоскостью, находящейся в диэлектрике с диэлектрической проницаемостью, равной
бесконечной плоскостью, находящейся в диэлектрике с диэлектрической проницаемостью, равной  . Напряженность электрического поля бесконечной равномерно заряженной плоскости:
. Напряженность электрического поля бесконечной равномерно заряженной плоскости:  , где
, где  =
=  – поверхностная плотность электрического заряда. Таким образом, напряженность электрического поля бесконечной равномерно заряженной плоскости не зависит от расстояния до нее. Плоскость может считаться бесконечной, если расстояние от нее пренебрежимо мало по сравнению с ее размерами. Только на таких расстояниях
– поверхностная плотность электрического заряда. Таким образом, напряженность электрического поля бесконечной равномерно заряженной плоскости не зависит от расстояния до нее. Плоскость может считаться бесконечной, если расстояние от нее пренебрежимо мало по сравнению с ее размерами. Только на таких расстояниях  не зависит от расстояния до плоскости.
не зависит от расстояния до плоскости.
12. Запишите выражение для напряженности электростатического поля между двумя параллельными равномерно заряженными разноименными и равными по модулю зарядами бесконечными плоскостями. Пространство между ними заполнено диэлектриком с диэлектрической проницаемостью, равной  . Поле двух параллельных бесконечных плоскостей, заряженных разноименно с одинаковой по величине постоянной поверхностной плоскостью
. Поле двух параллельных бесконечных плоскостей, заряженных разноименно с одинаковой по величине постоянной поверхностной плоскостью  , можно найти как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. В области между плоскостями складываемые поля имеют одинаковое направление, так что результирующая напряженность равна
, можно найти как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. В области между плоскостями складываемые поля имеют одинаковое направление, так что результирующая напряженность равна  . Вне объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулю. Таким образом, поле оказывается сосредоточенным между плоскостями. Напряженность поля во всех точках этой области одинакова по величине и по направлению.
. Вне объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулю. Таким образом, поле оказывается сосредоточенным между плоскостями. Напряженность поля во всех точках этой области одинакова по величине и по направлению.
13. Запишите в ыражение для напряженности электростатического поля, созданного равномерно заряженной (линейная плотность заряда –  ) бесконечной нитью, находящейся в диэлектрике с диэлектрической проницаемостью, равной
) бесконечной нитью, находящейся в диэлектрике с диэлектрической проницаемостью, равной  . Напряженность электрического поля бесконечной равномерно заряженной нити:
. Напряженность электрического поля бесконечной равномерно заряженной нити:  ( r ≤ R). Если r > R, рассматриваемая замкнутая поверхность не содержит внутри зарядов, вследствие чего Е(r) = 0.Таким образом, внутри равномерно заряженной цилиндрической поверхности бесконечной длины поле отсутствует. Напряженность поля вне поверхности определяется линейной плотностью заряда
( r ≤ R). Если r > R, рассматриваемая замкнутая поверхность не содержит внутри зарядов, вследствие чего Е(r) = 0.Таким образом, внутри равномерно заряженной цилиндрической поверхности бесконечной длины поле отсутствует. Напряженность поля вне поверхности определяется линейной плотностью заряда  и расстоянием r от оси цилиндра.
и расстоянием r от оси цилиндра.
14. Чему равна циркуляция вектора напряженности электростатического поля. Циркуляция вектора напряженности  по произвольному замкнутому контуру L в электростатическом поле равна нулю. Циркуляцией напряженности
по произвольному замкнутому контуру L в электростатическом поле равна нулю. Циркуляцией напряженности  называется линейный интеграл:
называется линейный интеграл: 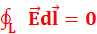 , где
, где  – напряженность поля в точках малого элемента контура длиной
– напряженность поля в точках малого элемента контура длиной  , а вектор
, а вектор  проведен в направлении обхода контура по касательной к нему.
проведен в направлении обхода контура по касательной к нему.
15. Как, зная зависимость электрического потенциала от координат, найти зависимость  от координат. Связи между потенциалом электростатического поля и напряженностью представлены следующими формулами:
от координат. Связи между потенциалом электростатического поля и напряженностью представлены следующими формулами:  или
или 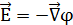 . Потенциал электростатического поля связан с напряженностью соотношением
. Потенциал электростатического поля связан с напряженностью соотношением  (проекция вектора
(проекция вектора  на произвольное направление l равна взятой с обратным знаком производной
на произвольное направление l равна взятой с обратным знаком производной  по l, т.е. скорости убывания потенциалов при перемещении вдоль направления l), где
по l, т.е. скорости убывания потенциалов при перемещении вдоль направления l), где  . В случае однородного поля
. В случае однородного поля  , где d – расстояние между двумя точками с потенциалами
, где d – расстояние между двумя точками с потенциалами  и
и  .
.
16. Как, зная зависимость  от координат, найти разность потенциалов между двумя точками. Связи между потенциалом электростатического поля и напряженностью представлены следующими формулами:
от координат, найти разность потенциалов между двумя точками. Связи между потенциалом электростатического поля и напряженностью представлены следующими формулами:  или
или 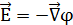 . Формула
. Формула 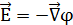 позволяет по известным значениям
позволяет по известным значениям  найти напряженность поля в каждой точке. Можно решить и обратную задачу, т.е. по заданным значениям
найти напряженность поля в каждой точке. Можно решить и обратную задачу, т.е. по заданным значениям  в каждой точке найти разность потенциалов между двумя произвольными точками поля:
в каждой точке найти разность потенциалов между двумя произвольными точками поля:  . Интеграл можно брать по любой линии, соединяющей точки 1 и 2, ибо работа сил поля не зависит от пути.
. Интеграл можно брать по любой линии, соединяющей точки 1 и 2, ибо работа сил поля не зависит от пути.
17. Какие поверхности называются эквипотенциальными. Как они проводятся. Как направлен вектор напряженности электростатического поля по отношению к эквипотенциальным поверхностям. Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Её уравнение имеет вид:  . При перемещении по эквипотенциальной поверхности на отрезок dl потенциал не изменяется (d
. При перемещении по эквипотенциальной поверхности на отрезок dl потенциал не изменяется (d  . Следовательно, согласно формуле
. Следовательно, согласно формуле  касательная к поверхности составляющая вектора напряженности равна нулю. Отсюда заключаем, что вектор напряженности в каждой точке направлен по нормали к эквипотенциальной поверхности, проходящей через данную точку. Приняв во внимание, что вектор напряженности направлен по касательной к линии напряженности, легко сообразить, что линии напряженности в каждой точке ортогональны к эквипотенциальным поверхностям. Эквипотенциальную поверхность можно провести через любую точку поля. Следовательно, таких поверхностей может быть построено бесконечное множество. Условливаются проводить поверхности таким образом, чтобы разность потенциалов для двух соседних поверхностей была всюду одна и та же. Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряженности поля. Там, где эти поверхности расположены гуще, там напряженность поля больше.
касательная к поверхности составляющая вектора напряженности равна нулю. Отсюда заключаем, что вектор напряженности в каждой точке направлен по нормали к эквипотенциальной поверхности, проходящей через данную точку. Приняв во внимание, что вектор напряженности направлен по касательной к линии напряженности, легко сообразить, что линии напряженности в каждой точке ортогональны к эквипотенциальным поверхностям. Эквипотенциальную поверхность можно провести через любую точку поля. Следовательно, таких поверхностей может быть построено бесконечное множество. Условливаются проводить поверхности таким образом, чтобы разность потенциалов для двух соседних поверхностей была всюду одна и та же. Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряженности поля. Там, где эти поверхности расположены гуще, там напряженность поля больше.
18. В чем состоит отличие связанных (поляризационных) зарядов от свободных (сторонних) зарядов. При рассмотрении электрических полей в различных средах различают два типа электрических зарядов – свободные и связанные. Связанными зарядами называются заряды, которые входят в состав атомов и молекул, а также заряды ионов в кристаллических диэлектриках с ионной решеткой. Под действием поля связанные заряды могут лишь немного смещаться из своих положений равновесия; покинуть пределы молекулы, в состав которой они входят, связанные заряды не могут. Заряды, которые, хотя и находятся в пределах диэлектрика, но не входят в состав его молекул, а также заряды, расположенные за пределами диэлектрика, называются свободными. Свободными зарядами являются заряды носителей тока в проводящих средах, положительные заряды атомных остатков в металлах и избыточные заряды, сообщенные телу и нарушающие его электрическую нейтральность.
19. Назовите виды поляризации. В зависимости от строения молекул (атомов) диэлектрика различают три вида поляризации:
- ориентационная (дипольная) поляризация, характерна для диэлектриков содержащих полярные молекулы. Проявляется как результат ориентации молекул, имеющих дипольные моменты, вдоль поля.
- электронная (деформационная) поляризация наблюдается в материалах также с неполярными молекулами. Осуществляется за счет деформации электронных орбит, что также приводит к появлению индуцированных дипольных моментов у атомов или молекул.
- ионная поляризация диэлектрика. Имеет место в материале, состоящем из неполярных молекул. Реализуется за счет смещения ионов из положения равновесия, в результате чего у молекулы возникает дипольный момент.
20. Что называется вектором поляризации (или поляризованности) диэлектрика. Количественной мерой поляризации диэлектрика служит вектор поляризованности  . Поляризованностью (вектором поляризации) называется отношение электрического дипольного момента малого объема диэлектрика к величине V этого объема:
. Поляризованностью (вектором поляризации) называется отношение электрического дипольного момента малого объема диэлектрика к величине V этого объема:  , где
, где  – дипольный момент материала в объеме V,
– дипольный момент материала в объеме V,  – дипольный момент одной молекулы.
– дипольный момент одной молекулы.
21. Какова связь между нормальной составляющей вектора поляризованности диэлектрика и поверхностной плотности связанных зарядов. Вследствие поляризации на поверхности диэлектрика появляются некомпенсированные связанные заряды, которые не могут перемещаться в отличие от свободных зарядов, способных перемещаться на макроскопические расстояния и участвовать в электропроводимости. Поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации:  .
.
22. какова связь между векторами напряженности электрического поля (Е), электрического смещения ( D ), поляризованности диэлектрика (Р). Д ля описания электрического поля системы зарядов с учетом поляризационных свойств диэлектриков вводится вектор электрического смещения. Связь между вектором поляризации Р, вектором напряженности электрического поля в диэлектрике Е и вектором электрического смещения (электрической индукции) в диэлектрике для изотропной среды записывается как 
23. Как связаны между собой тангенциальные составляющие вектора напряженности электрического поля на границе раздела двух диэлектриков. Напряженность электрического полянаправлена под некоторым углом к границе раздела. В таком случае вектор напряженности можно разложить на две составляющие, на нормальную -  и тангенциальную -
и тангенциальную -  . Нормальная составляющая при переходе из диэлектрика 1 в диэлектрик 2 изменяется (при переходе через границу двух диэлектриков претерпевает разрыв) согласно
. Нормальная составляющая при переходе из диэлектрика 1 в диэлектрик 2 изменяется (при переходе через границу двух диэлектриков претерпевает разрыв) согласно  , а тангенциальная не изменяется (при переходе через границу двух диэлектриков непрерывна)
, а тангенциальная не изменяется (при переходе через границу двух диэлектриков непрерывна)  . Здесь
. Здесь  – проекция вектора
– проекция вектора  на орт
на орт  , направленный вдоль линии пересечения плоскости раздела диэлектриков с плоскостью, в которой лежат векторы
, направленный вдоль линии пересечения плоскости раздела диэлектриков с плоскостью, в которой лежат векторы  и
и  . Заменив согласно
. Заменив согласно 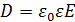 проекции вектора Е проекциями вектора D, деленными на
проекции вектора Е проекциями вектора D, деленными на  , получим соотношение
, получим соотношение  , из которого следует, что
, из которого следует, что  (тангенциальная составляющая вектора электрического смещения при переходе через границу двух диэлектриков претерпевает разрыв).
(тангенциальная составляющая вектора электрического смещения при переходе через границу двух диэлектриков претерпевает разрыв).
24. как связаны между собой нормальные составляющие вектора электрического смещения на границе раздела двух диэлектриков. Нормальная составляющая вектора электрического смещения при переходе через границу двух диэлектриков непрерывна:  . Здесь
. Здесь  – проекция на
– проекция на  вектора D в i-м диэлектрике в непосредственной близости к его границе с другим диэлектриком. Заменив согласно
вектора D в i-м диэлектрике в непосредственной близости к его границе с другим диэлектриком. Заменив согласно  проекции D соответствующими проекциями вектора E, умноженным на
проекции D соответствующими проекциями вектора E, умноженным на  , получим соотношение
, получим соотношение  или
или  (тангенциальная составляющая вектора напряженности при переходе через границу двух диэлектриков претерпевает разрыв).
(тангенциальная составляющая вектора напряженности при переходе через границу двух диэлектриков претерпевает разрыв).
25. Запишите условие равновесия зарядов в проводнике. Для равновесия зарядов на проводнике необходимо выполнение следующих условий: 1. Напряженность поля всюду внутри проводника должна быть равна нулю  . Это означает, что потенциал внутри проводника должен быть постоянным (
. Это означает, что потенциал внутри проводника должен быть постоянным (  . 2. Напряженность поля на поверхности проводника должна быть в каждой направлена по нормали к поверхности:
. 2. Напряженность поля на поверхности проводника должна быть в каждой направлена по нормали к поверхности:  . Следовательно, в случае равновесия зарядов поверхность проводника будет эквипотенциальной.
. Следовательно, в случае равновесия зарядов поверхность проводника будет эквипотенциальной.
26. Что такое электроемкость уединенного проводника. Привести формулу. Коэффициент пропорциональности С между потенциалом и зарядом называется электроемкостью (сокращенно просто емкостью) уединенного проводника. Из q=C  следует, что
следует, что  . Емкость численно равна заряду, сообщение которого проводнику повышает его потенциал на единицу. Емкость уединенного проводника зависит от геометрических размеров проводника, среды в котором он находится, от наличия других проводников вокруг него и не зависит от материала проводника.
. Емкость численно равна заряду, сообщение которого проводнику повышает его потенциал на единицу. Емкость уединенного проводника зависит от геометрических размеров проводника, среды в котором он находится, от наличия других проводников вокруг него и не зависит от материала проводника.
27. Как изменится емкость уединенного проводящего шара при переносе его из вакуума в среду с относительной диэлектрической проницаемостью  . Емкость уединенного шара радиуса R, погруженного в однородный безграничный диэлектрик с проницаемостью
. Емкость уединенного шара радиуса R, погруженного в однородный безграничный диэлектрик с проницаемостью  , равна
, равна  , где R – радиус шара.
, где R – радиус шара.
28. Запишите формулу, по которой можно найти электроемкость плоского конденсатора. Электрическая емкость плоского конденсатора, состоящая из двух близко расположенных параллельных пластин, пространство между которыми заполнено диэлектриком, выражается формулой  , где S – площадь обкладки, d – величина зазора между обкладками,
, где S – площадь обкладки, d – величина зазора между обкладками,  – диэлектрическая проницаемость вещества, заполняющего зазор. Отметим, что емкость реального плоского конденсатора определяется данной формулой с тем большей точностью, чем меньше зазор d по сравнению с линейными размерами обкладок. Также из формулы следует, что размерность электрической постоянной
– диэлектрическая проницаемость вещества, заполняющего зазор. Отметим, что емкость реального плоского конденсатора определяется данной формулой с тем большей точностью, чем меньше зазор d по сравнению с линейными размерами обкладок. Также из формулы следует, что размерность электрической постоянной 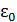 равна размерности электроемкости, деленной на размерность длины. В соответствии с этим
равна размерности электроемкости, деленной на размерность длины. В соответствии с этим 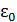 измеряется в фарадах на метр.
измеряется в фарадах на метр.
29. Запишите уравнения, по которым можно рассчитать энергию заряженного конденсатора. Воспользовавшись определением электроемкости конденсатора  можно написать три выражения для энергии заряженного конденсатора:
можно написать три выражения для энергии заряженного конденсатора: 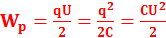 , где U – разность потенциалов (или электрическое напряжение) между обкладками конденсатора. Полученные формулы для энергии справедливы для любого (плоского, сферического, цилиндрического и т.д.) конденсатора.
, где U – разность потенциалов (или электрическое напряжение) между обкладками конденсатора. Полученные формулы для энергии справедливы для любого (плоского, сферического, цилиндрического и т.д.) конденсатора.
30. По каким уравнениям можно рассчитать объемную плотность энергии в однородном изотопном диэлектрике. Электрическое поле обладает энергией, которая распределена по всему объему пространства, где есть это поле. Соответственно энергия заряженного проводника или конденсатора является энергией их электрических полей. Энергия однородного поля распределена равномерно по его объему с объемной плотностью энергии, равной  , где D –электрическое смещение, E –напряженность электрического поля.
, где D –электрическое смещение, E –напряженность электрического поля.
СТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
1. Запишите закон Ома для однородного участка цепи. Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику, пропорциональна напряжению U на концах проводника:  , где R = const. Это соотношение выражает закон Ома для однородного участка цепи: сила тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения U на проводнике. Величину R принято называть электрическим сопротивлением.
, где R = const. Это соотношение выражает закон Ома для однородного участка цепи: сила тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения U на проводнике. Величину R принято называть электрическим сопротивлением.
2. Что такое электрический ток. Электрическим током называется упорядоченное движение электрических зарядов. За направление тока принимают направление движения положительных зарядов, которое противоположно направлению движения отрицательных зарядов. Различают: ток проводимости (ток в проводниках), конвекционный ток и ток в вакууме.
3. Назовите характеристики электрического тока и их единицы измерения. Количественной характеристикой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда dq, переносимого через поперечное сечение проводника за интервал времени dt, к этому интервалу времени:  .В международной системе единиц СИ сила тока измеряется в амперах (А).
.В международной системе единиц СИ сила тока измеряется в амперах (А).
В качестве характеристики, задающей распределение силы тока по поперечному сечению проводника служит вектор плотности тока 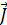 . Плотностью электрического тока называется вектор
. Плотностью электрического тока называется вектор 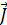 , совпадающий с направлением электрического тока в рассматриваемой точке и численно равный отношению силы тока dI сквозь малый элемент поверхности, перпендикулярной направлению тока, к площади dS⊥ этого элемента:
, совпадающий с направлением электрического тока в рассматриваемой точке и численно равный отношению силы тока dI сквозь малый элемент поверхности, перпендикулярной направлению тока, к площади dS⊥ этого элемента:  . Единицей измерения плотности тока является А/м2.
. Единицей измерения плотности тока является А/м2.
4. Назовите условия, выполнение которых необходимо для протекания в цепи электрического тока. Условия, необходимые для проявления и существования электрического тока проводимости в среде: а) наличие в среде свободных носителей заряда, т.е. заряженных частиц, способных перемещаться. В металле это электроны проводимости; в электролитах – положительные и отрицательные ионы; в газах – положительные, отрицательные ионы и электроны. б) наличие в среде электрического поля, энергия которого затрачивалась бы на перемещение электрических зарядов. Для того, чтобы ток был длительным, энергия электрического поля должна все время пополняться, т.е. нужен источник электрической энергии – устройство, в котором происходит преобразование какого-либо вида энергии в энергию электрического тока.
5. Какие силы по своей природе не могут быть сторонними. Если в цепи на носители тока действуют только силы электростатического поля (кулоновские), то происходит перемещение носителей (они предполагаются положительными) от точек с большим потенциалом к точкам с меньшим потенциалом. Это приведет к выравниванию потенциалов во всех точках цепи и к исчезновению электрического поля. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счет работы сил не электростатического происхождения. Такие устройства называются источниками тока. Силы не электростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними. Эти силы могут быть обусловлены химическими процессами, диффузией носителей тока в неоднородной среде или через границу двух разнородных веществ, электрическими полями, порождаемыми меняющимся во времени магнитным полем.
6. Чему равна циркуляция вектора напряженности сторонних сил. Вне источника напряженность поля сторонних сил отсутствует, т.е. равна нулю, поэтому при перемещении положительного заряда по замкнутой цепи работу сторонних сил можно представить как интеграл по всему замкнутому контуру  (
( – напряженность поля сторонних сил, определяемая сторонней силой, действующей на единичный положительный заряд внутри источника). Отсюда ЭДС, действующая в замкнутой цепи - циркуляция вектора напряженности поля сторонних сил:
– напряженность поля сторонних сил, определяемая сторонней силой, действующей на единичный положительный заряд внутри источника). Отсюда ЭДС, действующая в замкнутой цепи - циркуляция вектора напряженности поля сторонних сил: 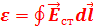 . Если цепь разомкнута, то ЭДС останется по величине такой же, поскольку определяется только на промежутке источника тока.
. Если цепь разомкнута, то ЭДС останется по величине такой же, поскольку определяется только на промежутке источника тока.
7. Запишите обобщенный закон Ома (закон Ома для неоднородного участка цепи). Для неоднородного участка цепи (участка, содержащего ЭДС), закон Ома записывается в следующей форме:  . Это соотношение принято называть обобщенным законом Ома. Обобщенный закон Ома выражает закон сохранения энергии применительно к участку цепи постоянного тока. Он в равной мере справедлив как для пассивных участков (не содержащих ЭДС), так и для активных.
. Это соотношение принято называть обобщенным законом Ома. Обобщенный закон Ома выражает закон сохранения энергии применительно к участку цепи постоянного тока. Он в равной мере справедлив как для пассивных участков (не содержащих ЭДС), так и для активных.
8. Запишите закон Ома для замкнутой цепи. Закон Ома для замкнутой цепи, содержащей источник ЭДС, запишется в виде:  . Эта формула выражает закон Ома для полной цепи: Сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
. Эта формула выражает закон Ома для полной цепи: Сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
9. Сформулируйте и запишите формулу закона Джоуля-Ленца (в интегральной или дифференциальной форме). Независимо друг от друга Джоуль и Ленца показали, что при протекании тока, в проводнике выделяется количество теплоты:  (работа электрического тока, протекающего по неподвижному проводнику с сопротивлением, преобразуется в тепло, выделяющееся на проводнике).Если ток изменяется со временем, то
(работа электрического тока, протекающего по неподвижному проводнику с сопротивлением, преобразуется в тепло, выделяющееся на проводнике).Если ток изменяется со временем, то  . Это закон Джоуля-Ленца в интегральной форме. Отсюда видно, что нагревание происходит за счет работы, совершаемой силами поля над зарядом.
. Это закон Джоуля-Ленца в интегральной форме. Отсюда видно, что нагревание происходит за счет работы, совершаемой силами поля над зарядом.
Закон Джоуля-Ленца в дифференциальной форме выражен следующей формулой:  (удельная тепловая мощность тока пропорциональна квадрату плотности электрического тока и удельному сопротивлению среды в данной точке).
(удельная тепловая мощность тока пропорциональна квадрату плотности электрического тока и удельному сопротивлению среды в данной точке).
Приведенные формулы справедливы для однородного участка цепи и для неоднородного при условии, что действующие в них сторонние силы имеют нехимическое происхождение.
10. Дайте определение вектора магнитной индукции, назовите ее размерность и приведите соответствующие формулы (через силу Ампера и через вращающийся момент). Вектор магнитной индукции  — векторная физическая величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства. Вектор магнитной индукции определяет силы, действующие на токи или движущиеся заряды в магнитном поле. В СИ единицей измерения магнитной индукции является тесла: 1 Тл = Дж/А·м2 = Н·м/А·м2 = Н/А·м Силовое действие магнитного поля может обнаруживаться по действию силы Ампера на прямолинейный проводник с током и по вращающемуся действию на замкнутый контур. При исследовании магнитного поля с помощью прямолинейного проводника с током магнитная индукция определяется следующим образом: модуль магнитной индукции равен отношению максимального значения модуля силы Ампера F, действующий на проводник с током, к силе тока I в проводнике и его длине l:
— векторная физическая величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства. Вектор магнитной индукции определяет силы, действующие на токи или движущиеся заряды в магнитном поле. В СИ единицей измерения магнитной индукции является тесла: 1 Тл = Дж/А·м2 = Н·м/А·м2 = Н/А·м Силовое действие магнитного поля может обнаруживаться по действию силы Ампера на прямолинейный проводник с током и по вращающемуся действию на замкнутый контур. При исследовании магнитного поля с помощью прямолинейного проводника с током магнитная индукция определяется следующим образом: модуль магнитной индукции равен отношению максимального значения модуля силы Ампера F, действующий на проводник с током, к силе тока I в проводнике и его длине l:  . При исследовании магнитного поля с помощью контура с током магнитная индукция определяется следующим образом: модуль вектора индукции
. При исследовании магнитного поля с помощью контура с током магнитная индукция определяется следующим образом: модуль вектора индукции  равен отношению максимального вращающегося момента сил М, действующего на рамку с током со стороны магнитного поля, к произведению силы тока I в рамке на ее площадь S:
равен отношению максимального вращающегося момента сил М, действующего на рамку с током со стороны магнитного поля, к произведению силы тока I в рамке на ее площадь S: 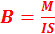 .
.
11. Что называется магнитным моментом контура с током. (приведите соответствующий момент). Магнитный момент контура с током(магнитный дипольный момент)— основная векторная величина, характеризующая магнитные свойства вещества:  ,где I - сила тока в контуре, S - площадь поверхности контура (рамки),
,где I - сила тока в контуре, S - площадь поверхности контура (рамки),  - единичный вектор нормали к поверхности рамки. Направление вектора
- единичный вектор нормали к поверхности рамки. Направление вектора  совпадает с направлением положительной нормали к контуру.
совпадает с направлением положительной нормали к контуру.
12. Запишите закон Био-Савара-Лапласа (формула и расшифровка всех величин, входящих в нее, привести рисунок). Закон Био — Савара — Лапласа для проводника с током I, элемент которого  l создает в некоторой точке А индукцию поля
l создает в некоторой точке А индукцию поля 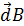 , записывается в виде
, записывается в виде  , где
, где  - магнитная постоянная, d
- магнитная постоянная, d  - вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током,
- вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током,  - радиус-вектор, проведенный из элемента d
- радиус-вектор, проведенный из элемента d  проводника в точку А поля, r — модуль радиуса-вектора
проводника в точку А поля, r — модуль радиуса-вектора  . Направление d
. Направление d  перпендикулярно d
перпендикулярно d  и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление d
и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление d  , если поступательное движение винта соответствует направлению тока в элементе.
, если поступательное движение винта соответствует направлению тока в элементе.

13. Приведите формулировку и математическую запись в интегральной форме закона полного тока (теорема о циркуляции) для магнитного поля в вакууме. Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора  ): циркуляция вектора
): циркуляция вектора  по произвольному замкнутому контуру равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром:
по произвольному замкнутому контуру равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром:  , где n — число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.
, где n — число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.
14. Поток вектора магнитной индукции (определение, математическая запись), размерность. Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярнаяфизическая величина, равная d Ф B =  = Bn dS, где Bn = В cosa — проекция вектора
= Bn dS, где Bn = В cosa — проекция вектора  на направление нормали к площадке dS (a — угол между векторами
на направление нормали к площадке dS (a — угол между векторами  и
и  ), dS = dSn — вектор, модуль которого равен dS, а направление совпадает с направлением нормали
), dS = dSn — вектор, модуль которого равен dS, а направление совпадает с направлением нормали  к площадке. Поток вектора
к площадке. Поток вектора  может быть как положительным, так и отрицательным в зависимости от знака cosa (определяется выбором положительного направления нормали
может быть как положительным, так и отрицательным в зависимости от знака cosa (определяется выбором положительного направления нормали  ). Поток вектора
). Поток вектора  связывают с контуром, по которому течет ток. В таком случае положительное направление нормали к контуру нами уже определено, оно связывается с током правилом правого винта. Таким образом, магнитный поток, создаваемый контуром через поверхность, ограниченную им самим, всегда положителен. Поток вектора магнитной индукции
связывают с контуром, по которому течет ток. В таком случае положительное направление нормали к контуру нами уже определено, оно связывается с током правилом правого винта. Таким образом, магнитный поток, создаваемый контуром через поверхность, ограниченную им самим, всегда положителен. Поток вектора магнитной индукции  через произвольную поверхность S равен
через произвольную поверхность S равен  =
=  Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору
Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору  , B n = B = const и
, B n = B = const и  = ВS. Из этой формулы определяется единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, проходящий через плоскую поверхность площадью 1 м2, расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл (1 Вб = 1 Тл·м2).
= ВS. Из этой формулы определяется единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, проходящий через плоскую поверхность площадью 1 м2, расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл (1 Вб = 1 Тл·м2).
15. Приведите формулировку и математическую запись в интегральной форме теоремы Остроградского – Гаусса для магнитного поля. Теорема Гаусса для вектора  : поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:  Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.
Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.
16. Запишите закон Ампера для силы взаимодействия двух параллельных токов. Два параллельных тока одинакового направления притягиваются друг к другу с силой dF =  Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая приведенной формулой.
Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая приведенной формулой.
17. Запишите закон Ампера для элемента проводника с током в магнитном поле в векторной форме. Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования магнитного поля на различные проводники с током, Ампер установил, что сила  , с которой магнитное поле действует на элемент проводника d
, с которой магнитное поле действует на элемент проводника d  с током, находящегося в магнитном поле, равна
с током, находящегося в магнитном поле, равна  , где
, где  – вектор, по модулю равный d
– вектор, по модулю равный d  и совпадающий по направлению с током,
и совпадающий по направлению с током,  – вектор магнитной индукции. Направление вектора
– вектор магнитной индукции. Направление вектора  может быть найдено по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор
может быть найдено по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор  , а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
18. Запишите выражение для силы Лоренца. Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд q, движущийся в магнитном поле со скоростью  , называется силой Лоренца и выражается формулой
, называется силой Лоренца и выражается формулой  , где
, где  – индукция магнитного поля, в котором заряд движется. Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор
– индукция магнитного поля, в котором заряд движется. Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор  , а четыре вытянутых пальца направить вдоль вектора
, а четыре вытянутых пальца направить вдоль вектора  (для q > 0 направления
(для q > 0 направления  совпадают, для q < 0 – противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд.
совпадают, для q < 0 – противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд.
19. Запишите выражение для работы, которая совершается при перемещении проводника с током в магнитном поле. Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником:  . Формула справедлива и для произвольного направления вектора
. Формула справедлива и для произвольного направления вектора  .
.
20. Запишите выражение для работы, которая совершается при перемещении контура с током в магнитном поле. Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром:  . Формула остается справедливой для контура любой формы в произвольном магнитном поле.
. Формула остается справедливой для контура любой формы в произвольном магнитном поле.
21. Запишите выражение для индукции магнитного поля (B) в центре кругового витка с током I и радиусом R. Магнитная индукция поля в центре кругового проводника с током равна  , где
, где  – магнитная постоянная, μ — магнитная проницаемость среды, в которой находится проводник, I – сила тока в проводнике, R – радиус кругового витка.
– магнитная постоянная, μ — магнитная проницаемость среды, в которой находится проводник, I – сила тока в проводнике, R – радиус кругового витка.
22. Запишите выражение для индукции магнитного поля (B), создаваемого прямым бесконечным проводником с током в произвольной точке. Для прямолинейного бесконечно длинного проводника с током симметрия линий напряженности и индукции в изотропной среде позволяет определить величину магнитного поля в любой точке на расстоянии R от оси проводника. Линии напряженности и магнитной индукции поля прямолинейного проводника представляют собой концентрические окружности, лежащие в плоскостях, перпендикулярных проводнику. Вдоль линии напряженность (индукция) магнитного поля одинакова и циркуляция равна произведению напряженности (индукции) на длину линии. Соответственно магнитная индукция поля прямого тока равна  , где
, где  – магнитная постоянная, μ — магнитная проницаемость среды, в которой находится проводник, I – сила тока в проводнике, R – расстояние до проводника.
– магнитная постоянная, μ — магнитная проницаемость среды, в которой находится проводник, I – сила тока в проводнике, R – расстояние до проводника.
23. Что называется вектором намагниченности (J). (формула, размерность). Вещество, помещенное во внешнее магнитное поле, намагничивается. Степень намагничения вещества принято характеризовать вектором намагничения 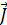 . Вектором намагниченности (намагничения) называется физическая величина, численно равная суммарному магнитному моменту единицы объема вещества:
. Вектором намагниченности (намагничения) называется физическая величина, численно равная суммарному магнитному моменту единицы объема вещества:  , где
, где 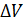 – физически бесконечно малый объем, взятый в окрестности рассматриваемой точки,
– физически бесконечно малый объем, взятый в окрестности рассматриваемой точки,  – магнитный момент отдельной молекулы. Суммирование производится по всем молекулам, заключенным в объеме
– магнитный момент отдельной молекулы. Суммирование производится по всем молекулам, заключенным в объеме 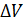 . В СИ имеет название ампер на метр и обозначается А/м.
. В СИ имеет название ампер на метр и обозначается А/м.
24. Запишите формулу, связывающую магнитную индукцию В в магнетике с магнитной проницаемостью  и напряженностью магнитного поля Н в этом магнетике. Вектор напряженности магнитного поля
и напряженностью магнитного поля Н в этом магнетике. Вектор напряженности магнитного поля  является дополнительным вектором к силовому вектору индукции магнитного поля
является дополнительным вектором к силовому вектору индукции магнитного поля  . Векторы
. Векторы  и
и  между собой связаны наподобие векторов напряженности электрического поля
между собой связаны наподобие векторов напряженности электрического поля  и электрического смещения
и электрического смещения  . А именно, для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением:
. А именно, для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением: 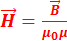 , где m0 — магнитная постоянная, m — безразмерная величина — магнитная проницаемость среды,показывающая, во сколько раз магнитное поле макротоков
, где m0 — магнитная постоянная, m — безразмерная величина — магнитная проницаемость среды,показывающая, во сколько раз магнитное поле макротоков  усиливается за счет поля микротоков среды. Таким образом, напряженность магнитного поля
усиливается за счет поля микротоков среды. Таким образом, напряженность магнитного поля  есть вектор, имеющий то же направление, что и вектор
есть вектор, имеющий то же направление, что и вектор  , но в
, но в  раз меньший по модулю (в анизотропных средах векторы
раз меньший по модулю (в анизотропных средах векторы  и
и  , вообще говоря, не совпадают по направлению).
, вообще говоря, не совпадают по направлению).
25. Запишите формулу, связывающую векторы намагниченности и напряженности магнитного поля. Вектор намагниченности принято связывать не с магнитной индукцией, а с напряженностью поля. Вектор намагничения пропорционален напряженности магнитного поля  , вызывающего намагничение
, вызывающего намагничение  , где
, где  – характерная для данного магнетика величина, называемая магнитной восприимчивостью вещества, численно равная величине вектора намагниченности магнетика при напряженности магнитного поля равной единице. Следовательно, магнитная восприимчивость парамагнетиков положительна (
– характерная для данного магнетика величина, называемая магнитной восприимчивостью вещества, численно равная величине вектора намагниченности магнетика при напряженности магнитного поля равной единице. Следовательно, магнитная восприимчивость парамагнетиков положительна ( ), диамагнетиков – отрицательна (
), диамагнетиков – отрицательна ( ).
).
26. Сформулируйте закон полного тока (теорема о циркуляции) для магнитного поля в веществе и запишите его математическое выражение в интегральной форме. Теорема о циркуляции вектора магнитной индукции (закон полного тока): циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна произведению магнитной постоянной μ0 на алгебраическую сумму токов, охватываемых этим контуром:  ,где n — число проводников с токами, которые охватываются контуром L любой формы. Каждый ток в уравнении учитывается столько раз, сколько раз он охватывается контуром. Ток считается положительным, если его направление образует с направлением обхода по контуру правовинтовую систему; отрицательным считается ток противоположного направления. Закон полного тока является интегральной формулировкой закона Био-Савара и входит в систему уравнений Максвелла.
,где n — число проводников с токами, которые охватываются контуром L любой формы. Каждый ток в уравнении учитывается столько раз, сколько раз он охватывается контуром. Ток считается положительным, если его направление образует с направлением обхода по контуру правовинтовую систему; отрицательным считается ток противоположного направления. Закон полного тока является интегральной формулировкой закона Био-Савара и входит в систему уравнений Максвелла.
27. Назовите типы магнетиков. В зависимости от знака и величины магнитной восприимчивости все магнетики подразделяются на три группы: 1) диамагнетики, у которых χ отрицательна мала по абсолютной величине (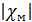
 ; 2) парамагнетики, у которых χ тоже невелика, но положительна (
; 2) парамагнетики, у которых χ тоже невелика, но положительна (
 3) ферромагнетики, у которых χ положительна и достигает очень больших значений (
3) ферромагнетики, у которых χ положительна и достигает очень больших значений ( 1
1  ). Кроме того, в отличие от диа- и парамагнетиков, для которых χ не зависти от
). Кроме того, в отличие от диа- и парамагнетиков, для которых χ не зависти от  , восприимчивость ферромагнетиков является функцией напряженности магнитного поля.
, восприимчивость ферромагнетиков является функцией напряженности магнитного поля.
28. Что называется спином электрона. Существование собственных моментов электрона первоначально пытались объяснить, рассматривая электрон как заряженный шарик, вращающийся вокруг своей оси. В соответствии с этим собственный механический момент электрона получил название СПИН (от англ. to spin – вращаться). Однако вскоре обнаружилось, что такое представление приводит к ряду противоречий, и от гипотезы о «вращающемся» электроне пришлось отказаться. В настоящее время принимается, что собственный механический момент (спин) и связанный с ним собственный (спиновый) магнитный момент являются такими же неотъемлемыми свойствами электрона, как и его масса и заряд. И так, электрон, обладающий собственным механическим моментом импульса  , называется спином. Спину электрона соответствует собственный (спиновый) магнитный момент
, называется спином. Спину электрона соответствует собственный (спиновый) магнитный момент  . Проекция спина на направление вектора
. Проекция спина на направление вектора 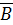 может принимать только одно из следующих двух значений
может принимать только одно из следующих двух значений  , где ħ =
, где ħ =  (h – постоянная Планка),
(h – постоянная Планка), 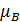 – магнетон Бора, являющийся единицей магнитного момента электрона.
– магнетон Бора, являющийся единицей магнитного момента электрона.
29. Приведите закон преломления линий вектора  на границе раздела двух магнетиков. Вблизи поверхности раздела двух магнетиков векторы
на границе раздела двух магнетиков. Вблизи поверхности раздела двух магнетиков векторы  и
и  должны удовлетворять определенным граничным условиям, которые вытекают из соотношений
должны удовлетворять определенным граничным условиям, которые вытекают из соотношений  B = 0,
B = 0,  = j. В соответствии с тем, что
= j. В соответствии с тем, что  B = 0, поток вектора
B = 0, поток вектора  через любую замкнутую поверхность равен нулю. Сосчитаем поток вектора
через любую замкнутую поверхность равен нулю. Сосчитаем поток вектора  через поверхность малого цилиндра, охватывающего границу раздела 2-х сред:
через поверхность малого цилиндра, охватывающего границу раздела 2-х сред:  =0, где S - площадь основания цилиндра,
=0, где S - площадь основания цилиндра,  - площадь боковой поверхности. Устремляя высоту цилиндра h → 0 и,
- площадь боковой поверхности. Устремляя высоту цилиндра h → 0 и,  → 0 получаем на границе:
→ 0 получаем на границе:  и, учитывая, что
и, учитывая, что  и
и  - противоположно направленные нормали, и вводя общую нормаль, имеем:
- противоположно направленные нормали, и вводя общую нормаль, имеем:  Итак: нормальные составляющие вектора
Итак: нормальные составляющие вектора  непрерывны на границе раздела двух магнетиков.
непрерывны на границе раздела двух магнетиков.
Date: 2016-11-17; view: 585; Нарушение авторских прав