Доказательство теоремы

Необходимость. Система нетривиально совместна. Это означает, что существуют числа не все равные нулю, для которых справедливо . Последнее равенство означает, что n столбцов матрицы систем линейно зависимы и, следовательно, ранг матрицы системы (максимальное число линейно независимых столбцов) меньше числа столбцов, меньше числа неизвестных. Необходимость доказана.

Достаточность. Пусть ранг r матрицы системы меньше числа n неизвестных. По теореме о базисном миноре из этого следует, что существует отличный от нуля минор матрицы порядка r. Не умаляя общности, будем полагать, что базисный минор — главный минор матрицы

Рассмотрим первые r уравнений системы (по теореме о базисном миноре остальные уравнения — линейные комбинации этих первых уравнений):

Оставим слева первые r неизвестных, а остальные n-r неизвестные перенесем вправо и получим неоднородную систему линейных уравнений относительно неизвестных :

Определитель полученной системы — отличный от нуля базисный минор M_r.

Уравнения системы справедливы при произвольных значениях переменных Их естественно называть свободными. А переменные в левой части уравнений системы естественно назвать базисными.

Базисные переменные можно вычислить по формулам Крамера , i = 1, 2, …, r. Здесь 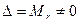— определитель матрицы системы, а — определитель, полученный из M_r заменой i- го столбцом правых частей. Вычислим, например, x ₁.

Здесь — некоторые числа.

Итак, . Аналогично — т.е. базисные переменные линейно выражаются через свободные переменные.

Положим, например такие значения свободных переменных:

Тогда вектор — отличное от тождественного нуля решение однородной системы . Т.е. однородная система нетривиально совместна. Теорема доказана.

Фундаментальная система решений однородной системы. Структура общего решения однородной системы

Вспомним, что решения однородной системы — векторы из Rⁿ. Вспомним также, что в силу свойств решений линейной однородной системы множество L ее решений — линейное подпространство в Rⁿ. Действительно: если и — два решения однородной системы , то при любых действительных числах α и β вектор 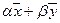— решение системы , иначе говоря, для любых и и любого числах α и . Доказано также, что если ранг r матрицы системы меньше числа неизвестных n, то система имеет ненулевые решения.

Определение. Выражение, позволяющее вычислить все (любое) решения системы, называется общим решением системы.

В теореме о нетривиальной совместности однородной системы показано, что если r — ранг матрицы системы, то r базисных переменных выражаются через свободные переменные по формулам

, .

Здесь для простоты полагали, что базисные переменные — это первые r переменных. Вообще говоря, это могут быть любые r переменных.

Итак, , — т.е. базисные переменные линейно выражаются через свободные переменные.

Построим n-r ненулевых решений однородной системы специальным образом.

Сначала положим и полученное решение обозначим .

Затем положим и полученное решение обозначим ,

и т.д., и, наконец, положим и полученное решение обозначим . Имеем (см. док-во теоремы о нетривиальной совместности)

.

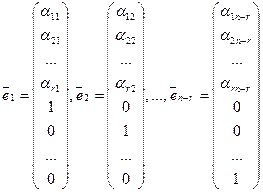Нетрудно видеть, что эти n-r ненулевые решения линейно независимы.

Действительно, запишем матрицу, столбцами которой являются векторы :

.

Минор этой матрицы, расположенный в последних n-r строках равен 1, отличен от нуля. Это означает, что ранг матрицы равен n-r и что ее n-r столбца линейно независимы. А столбцы этой матрицы — ненулевые решения однородной системы .

С другой стороны, любое решение системы, в соответствии с приведенными выше формулами, можно записать в виде:

Здесь произвольные значения свободных переменных обозначены буквами .

Подведем итог:

ü построена система , состоящая из n-r линейно независимых решений однородной системы;

ü любое решение системы линейно выражается через решения ;

ü множество решений однородной системы — линейное подпространство.

Тогда можно утверждать:

1. размерность подпространства L решений однородной системы равна n­­­ – r, где n — число неизвестных, r = RgA:dimL= n – r;

2. система — базис в подпространстве L решений однородной системы ;

3. выражение — общее решение однородной системы.

Определение. Система , состоящая из n-r линейно независимых решений однородной системы , , 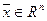RgA=r, называется фундаментальной системой решений однородной системы.

Выше мы доказали следующие утверждения.

Утверждение. Фундаментальная система решенийоднородной системы — базис пространства решений однородной системы.

Теорема о структуре общего решения однородной системы линейных алгебраических уравнений. Если ранг r матрицы однородной системы линейных уравнений меньше числа неизвестных n, то общее решение системы можно записать в виде линейной комбинации решений фундаментальной системы: .

Пример 1. Исследуем однородную систему линейных алгебраических уравнений

Исследовать однородную систему — ответить на вопрос является ли система нетривиально совместной, и если является, то найти ее общее решение.

Решение. Решим задачу методом Гаусса-Жордана.

Приведем матрицу системы к ступенчатому виду, выполняя элементарные преобразования строк (прямой ход метода Гаусса):

Ранг матрицы системы равен r = 2, число неизвестных n =4, r < n — система нетривиально совместна. Кроме того, очевидно, множества решений исходной системы и системы с преобразованной матрицей совпадают.

Продолжим преобразование матрицы системы, выполняя элементарные операции со строками так, чтобы базисный минор матрицы стал единичным (обратный ход метода Гаусса):

.

Запишем эквивалентную систему уравнений:

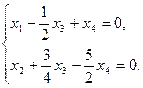
Главный минор матрицы этой системы — .

Следовательно, переменные — базисные переменные, а — свободные.

Перенесем свободные переменные вправо:

Получили выражение базисных переменных через свободные. Такое выражение — общее решение однородной системы, записанное «на языке систем».

Найдем базис в подпространстве решений системы (фундаментальную систему). Для этого положим значения свободных переменных равными и вычислим базисные переменные:

Тогда вектор — решение однородной системы.

Затем положим значения свободных переменных равными и вычислим базисные переменные:

Тогда вектор — решение однородной системы.

Векторы — линейно независимые решения однородной системы размерность пространства решений которой d = n – r = 4 – 2 = 2, т.е. — базис пространства решений.

Запишем общее решение системы:

.

Проверим:

Верно.

Ответ: Общее решение системы , — произвольные постоянные. Базис в пространстве решений системы — , .

Структура общего решения неоднородной системы

Вспомним одно из свойств решений линейной неоднородной системы:

Если и — два решения системы , то вектор — решение приведенной однородной системы .

Поскольку выражение задает все решения однородной системы, то для любых двух решений и неоднородной системы справедливо

и, следовательно, выражение позволяет вычислить любое решение неоднородной системы.

Таким образом доказана теорема о структуре общего решения линейной неоднородной системы.

Теорема о структуре общего решения неоднородной системы линейных алгебраических уравнений. Если ранг r матрицы неоднородной системы линейных уравнений меньше числа неизвестных n, то общее решение системы можно записать в виде

где 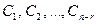— произвольные константы, а — фундаментальная система решений приведенной однородной системы, — некоторое известное (частное) решение неоднородной системы.

Пример 2. Исследуем неоднородную систему линейных алгебраических уравнений

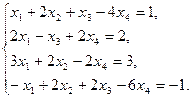
Исследовать неоднородную систему — ответить на вопрос является ли система совместной, и если является, то найти ее общее решение.

Решение. Решим задачу методом Гаусса-Жордана.

Приведем расширенную матрицу системы к ступенчатому виду, выполняя элементарные преобразования строк (прямой ход метода Гаусса):

Ранг расширенной матрицы системы равен рангу матрицы системы и равен двум:

RgA_p =RgA = r = 2, система совместна. Число неизвестных n =4, r < n — приведенная однородная система нетривиально совместна.

Кроме того, очевидно, множества решений исходной системы и системы с преобразованной матрицей совпадают.

Продолжим преобразование расширенной матрицы системы, выполняя элементарные операции со строками так, чтобы базисный минор матрицы стал единичным (обратный ход метода Гаусса):

.

Запишем эквивалентную систему уравнений:

Как и в примере 1, переменные — базисные переменные, а — свободные.

Перенесем свободные переменные вправо:

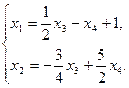
Получили выражение базисных переменных через свободные переменные. Такое выражение — общее решение неоднородной системы, записанное «на языке систем».

Найдем частное решение неоднородной системы. Для этого положим значения свободных переменных равными 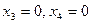и вычислим базисные переменные:

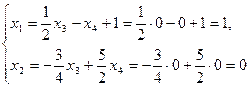
и тогда вектор — частное решение неоднородной системы.

Приведенная однородная система — система из примера 1.

Воспользуемся решением предыдущего примера:

, — фундаментальная система приведенной однородной системы, — общее решение приведенной однородной системы.

Тогда

Проверим:

Верно.

Ответ: Система совместна, ее общее решение

Вычисление обратной матрицы методом Гаусса-Жордана

Пусть A — обратимая квадратная матрица. Обозначим — j- й столбец обратной матрицы. Тогда, поскольку A∙A ^-1= E, то, очевидно, справедливо:

т.е. — матрица-столбец, все элементы которой, кроме j -го равны нулю, а элемент, расположенный в j -й строке равен единице.

Эти n систем можно решать методом Гаусса-Жордана одновременно, поскольку у всех у них одна и та же матрица.Запишем матрицу, содержащую в первых n столбцах матрицу системы, а в последних n столбцах — единичную матрицу, и выполним Гауссово исключение так, чтобы получилось:

Матрица, расположенная в последних n столбцах — обратная матрица. Действительно, в (n +1)-м столбце — решение системы 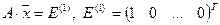, т.е. первый столбец обратной матрицы, в (n +2)-м столбце — решение системы , т.е. второй столбец обратной матрицы, и т.д., в (n + n)-м столбце — решение системы , т.е. n- й столбец обратной матрицы.

Пример 3. Найдем методом Гаусса-Жордана матрицу, обратную к матрице .

Решение

Т.е. .

Проверим.

Верно. Ответ: .

Date: 2016-11-17; view: 306; Нарушение авторских прав