Доказательство теоремы

Доказательство теоремы

Рассмотрим произвольные векторы из образа линейного оператора: и . Это означает: и такие, что и .

A — линейный оператор, следовательно, т.е. ;

для любого числа , т.е. . Теорема доказана.

Определение. Размерность образа линейного оператора называется рангом оператора, обозначается Rg( A ): r=Rg( A )=dim Im( A ).

Определение. Ядром линейного оператора называется множество элементов пространства Rⁿ, образом которых является нулевой элемент. Ядро оператора обозначают Ker (A): .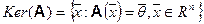

Теорема. Ядро линейного оператора — линейное подпространство пространства Rⁿ.

Доказательство теоремы

Рассмотрим произвольные векторы ядра линейного оператора: и . Это означает: и .

A — линейный оператор, следовательно, т.е. ;

для любого числа , т.е. . Теорема доказана.

Определение. Размерность ядра линейного оператора называется дефектом оператора, обозначается def(A): r= def(A)=dim Ker (A).

Длялинейного оператора , действующего из пространства Rⁿ в пространство R^m, справедливы следующие утверждения:

1) ранг оператора равен рангу его матрицы;

2) ядро оператора совпадает с множеством решений линейной однородной системы с матрицей A; размерность пространства решений этой системы равна дефекту оператора, а ее фундаментальная система решений образует базис в ядре оператора;

столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора.

Эти утверждения позволяют описать структуру образа и ядра линейного оператора (найти размерность подпространства и построить его базис), заданного матрицей, на языке матричных преобразований и общей теории линейных систем.

Примеры. Ядро и образнулевого оператора: поскольку то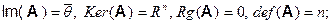

ядро и образ тождественного (единичного) оператора: поскольку , то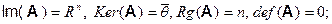

ядро и образ оператора проектирования пространства Rⁿ на подпространство R^n-1 параллельно вектору : поскольку , то

ядро и образ оператора поворота пространства R³ против часовой стрелки на угол π относительно оси вектора 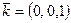: поскольку , то

Пример. Найдем ранг, дефект и базис ядра линейного оператора A, заданного в некотором базисе в R ³ матрицей .

Решение. Приведем матрицу оператора к ступенчатому виду:

.

Следовательно, , .

Ядро оператора описывается равенством .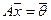

Методом Гаусса получили выражение для общего решения: или, что то же самое, .

Найдем ФСР (базис в пространстве решений однородной системы): .

Базис в пространстве решений однородной системы 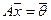— это и есть базис в ядре оператора A, заданного в некотором базисе в R ³ матрицей A.

Ответ: , ,

базис в ядре оператора образуют векторы .

Date: 2016-11-17; view: 235; Нарушение авторских прав