
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Механические колебания
|
|
Основные формулы
· Уравнение гармонических колебаний:
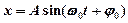 ,
,
где  – смещение точки от положения равновесия, А – амплитуда колебаний,
– смещение точки от положения равновесия, А – амплитуда колебаний, 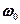 – круговая (циклическая частота), t – время,
– круговая (циклическая частота), t – время, 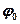 – начальная фаза колебаний.
– начальная фаза колебаний.
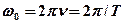 ,
,
где 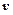 – частота колебаний,
– частота колебаний,  – период колебаний.
– период колебаний.
· Скорость и ускорение при гармонических колебаниях:
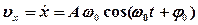 ,
,
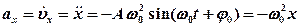 .
.
· Возвращающая сила
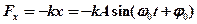 ,
,
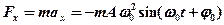 ,
,
где  – коэффициент упругой (квазиупругой) силы,
– коэффициент упругой (квазиупругой) силы,  – масса материальной точки.
– масса материальной точки.
· Максимальная возвращающая сила
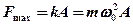
· Кинетическая энергия колеблющейся точки
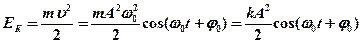
· Потенциальная энергия колеблющейся точки
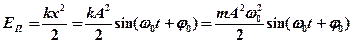
· Полная энергия при гармонических колебаниях:
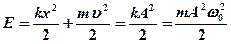 .
.
· Периоды колебаний:
 – математический маятник (
– математический маятник (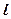 – длина нити,
– длина нити, 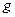 - ускорение свободного падения),
- ускорение свободного падения),
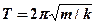 – пружинный маятник (
– пружинный маятник ( – масса тела,
– масса тела,  – жесткость пружины),
– жесткость пружины),
 – физический маятник (
– физический маятник (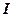 – момент инерции тела относительно оси, проходящей через точку подвеса,
– момент инерции тела относительно оси, проходящей через точку подвеса,  – масса тела,
– масса тела,  – расстояние от точки подвеса до центра масс).
– расстояние от точки подвеса до центра масс).
· Уравнение затухающих колебаний:
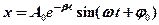 ,
,
где 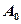 – амплитуда колебаний в начальный момент времени,
– амплитуда колебаний в начальный момент времени, 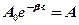 - амплитуда затухающих колебаний,
- амплитуда затухающих колебаний,  -коэффициент затухания (
-коэффициент затухания (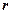 - коэффициент сопротивления,
- коэффициент сопротивления,  -масса точки),
-масса точки),  - частота затухающих колебаний.
- частота затухающих колебаний.
· Логарифмический декремент затухания
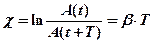 .
.
· Амплитуда результирующего колебания, полученного при сложении двух колебаний одинаковой частоты и одного направления:
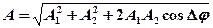 ,
,
где  и
и 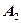 - амплитуды слагаемых колебаний,
- амплитуды слагаемых колебаний,  - разность фаз слагаемых колебаний.
- разность фаз слагаемых колебаний.
· Начальная фаза результирующего колебания определяется из формулы:

 .
.
· Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с одинаковыми частотами:
 ,
,
где  - разность фаз складываемых колебаний.
- разность фаз складываемых колебаний.
ЗАДАНИЯ
4.1. Уравнение движения точки дано в виде  м. Найти период, амплитуду, начальную фазу, циклическую частоту и частоту колебаний. [1с; 0,1м;
м. Найти период, амплитуду, начальную фазу, циклическую частоту и частоту колебаний. [1с; 0,1м; 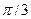 ; 2
; 2  ; 1 Гц]
; 1 Гц]
4.2 Написать уравнение гармонических колебаний точки с амплитудой 0,1 м, если начальная фаза равна  , а период колебаний 2 с.
, а период колебаний 2 с.
4.3 Написать уравнение гармонических колебаний точки с амплитудой 5 см, если за 2 минуты совершается 120 колебаний, а начальная фаза равна 60º.
4.4 Уравнение движения точки дано в виде 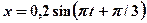 м. Найти максимальные значения скорости и ускорения.[
м. Найти максимальные значения скорости и ускорения.[ 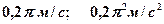 ]
]
4.5 Точка совершает гармонические колебания с амплитудой 10 см и периодом 5 с. Определить максимальную скорость и максимальное ускорение. [12,6 см/с; 15,8 см/с2]
4.6. Определите максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой 2 см и периодом 2 с. [0,0628 м/c; 0,197 м/ 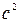 ]
]
4.7. Точка совершает гармонические колебания с периодом 8 с и начальной фазой, равной нулю. Определите, за какое время точка сместится от положения равновесия на половину амплитуды. [4/3 c]
4.8. Точка совершает гармонические колебания с периодом 12 с. Определите, за какое время скорость точки увеличится от нуля до половины максимального значения. [1 c]
4.9. Точка совершает гармонические колебания с периодом 12 c. Определите, за какое время ускорение точки увеличится от нуля до половины максимального значения. [1 c]
4.10. Уравнение движения точки дано в виде 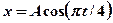 . Определите моменты времени, при которых достигается максимальная скорость точки. [2с, 6с, 10с …]
. Определите моменты времени, при которых достигается максимальная скорость точки. [2с, 6с, 10с …]
4.11. Уравнение движения точки дано в виде  . Определите моменты времени, при которых достигается максимальное ускорение точки. [0c, 2c, 4c …]
. Определите моменты времени, при которых достигается максимальное ускорение точки. [0c, 2c, 4c …]
4.12. Материальная точка совершает гармонические колебания согласно уравнению 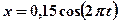 м. Определите максимальное значение модуля возвращающей силы и полную энергию точки, если её масса 0,1 кг. [0,59 Н; 0,047 Дж]
м. Определите максимальное значение модуля возвращающей силы и полную энергию точки, если её масса 0,1 кг. [0,59 Н; 0,047 Дж]
4.13. Материальная точка массой 50 г совершает гармонические колебания согласно уравнению  м. Определите возвращающую силу для момента времени 2 с. [0,11 Н]
м. Определите возвращающую силу для момента времени 2 с. [0,11 Н]
4.14. Определите отношение кинетической энергии точки, совершающей гармонические колебания, к её потенциальной энергии для моментов времени: a) t=T /12; б) t=T /8; в) t=T /6, где Т – период колебаний. Начальная фаза равна нулю. [3; 1; 1/3]
4.15. Определите отношение кинетической энергии точки, совершающей гармонические колебания, к её потенциальной энергии для моментов времени, при которых смещение от положения равновесия составляет: а) х=А /4; б) х=А /2; в) х=А, где А – амплитуда колебаний. [15; 3; 0]
4.16. Как изменится частота колебаний груза, висящего на двух одинаковых пружинах, если от их последовательного соединения перейти к параллельному? [увеличится в 2 раза]
4.17. Груз, подвешенный к пружине, колеблется по вертикали с амплитудой 8 см. Определите жёсткость пружины, если известно, что максимальная кинетическая энергия груза равна 0,8 Дж. [k=250 Н/м]
4.18. Если увеличить массу груза, подвешенного на пружине, на 600 г, то период колебаний возрастёт в 2 раза. Определите массу первоначально подвешенного груза. [200 г]
4.19. Два математических маятника, длины которых отличаются на 16 см, совершают за одно и то же время один 10 колебаний, другой 6 колебаний. Определите длины маятников. [9см; 25см]
4.20. Математический маятник длиной 1 м подвешен к потолку кабины, которая начинает опускаться вертикально вниз с ускорением  . Найдите период колебаний этого маятника. [2,32 с]
. Найдите период колебаний этого маятника. [2,32 с]
4.21. На какую высоту надо поднять математический маятник, чтобы период его колебаний увеличился в 2 раза? Радиус Земли 6400 км. [ 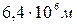 ]
]
4.22. Маятник, состоящий из невесомой нити длиной 1 м и свинцового шарика радиусом 0,02 м, совершает гармонические колебания с амплитудой 0,06 м. Определите: а) модуль максимального значения возвращающей силы; б) модуль максимальной скорости. Плотность свинца 11,3.103 кг/м3.
[0,22 Н; 0,18 м/с]
4.23. Тонкий обруч радиусом 0,5 м подвешен на вбитый в стенку гвоздь и совершает гармонические колебания в плоскости, параллельной стене. Определите частоту колебаний обруча. [0,5 Гц]
4.24. Однородный диск радиусом 20 см колеблется около горизонтальной оси, проходящей на расстоянии 15 см от центра диска. Определите период колебаний диска относительно этой оси. [1,07 с]
4.25. Диск радиусом 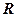 подвешен так, что может совершать гармонические колебания относительно образующей диска. Определите период и частоту колебаний диска.
подвешен так, что может совершать гармонические колебания относительно образующей диска. Определите период и частоту колебаний диска.
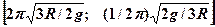
4.26. Тонкий стержень длиной 60 см совершает колебания относительно оси, отстоящей на расстоянии 15 см от его середины. Определите период колебаний стержня. [1,19 с]
4.27. Определите амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями: 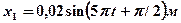 и
и 
[  ;
;  ]
]
4.28.Найдите уравнение результирующего колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями: 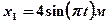 ,
, 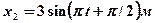 . [
. [ 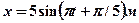 ]
]
4.29. Точка участвует в двух колебаниях одинаковой частоты одного направления и с одинаковыми начальными фазами. Амплитуды колебаний соответственно равны 3 см и 4 см. Определите амплитуду результирующего колебания.[7 см;]
4.30. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, которые происходят по законам:  и
и 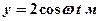 . Найдите траекторию движения точки. [окружность радиусом 2
. Найдите траекторию движения точки. [окружность радиусом 2  ]
]
4.31. Точка участвует в двух колебаниях одинаковой частоты и с одинаковыми начальными фазами, совершаемых во взаимно перпендикулярных направлениях. Амплитуды колебаний соответственно равны 3 см и 4 см. Определите амплитуду результирующего колебания. [5 см]
4.32. Запишите уравнение результирующего колебания точки, полученного от сложения двух взаимно перпендикулярных колебаний одинаковой частоты 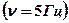 , с одинаковыми начальными фазами, равными
, с одинаковыми начальными фазами, равными 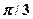 и с амплитудами:
и с амплитудами:  и
и  . [
. [ 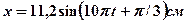 ]
]
4.33. Уравнение затухающих колебаний точки дано в виде 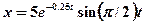 м. Определите скорость точки в моменты времени, равные
м. Определите скорость точки в моменты времени, равные  . [7,85 м/с; 2,9 м/с; 1,1 м/с]
. [7,85 м/с; 2,9 м/с; 1,1 м/с]
4.34. Логарифмический декремент затухания математического маятника равен 0,2. Во сколько раз уменьшится амплитуда за одно полное колебание? [в 1,22 раз]
4.35. Начальная амплитуда затухающих колебаний точки равна 3 см. По истечении 10 с от начала колебаний амплитуда стала равной 1 см. Через какое время амплитуда станет равной 0,3 см? [21 c]
4.36. Амплитуда затухающих колебаний маятника за 2 минуты уменьшилась в 2 раза. Определите коэффициент затухания. [5,78.10-3 1/с]
4.37. Амплитуда затухающих колебаний маятника за 1 минуту уменьшилась в 3 раза. Во сколько раз она уменьшится за 4 минуты? [в 81 раз]
Date: 2016-11-17; view: 739; Нарушение авторских прав