Уравнение Шредингера

Состояние в квантовой механике описывается с помощью некоторой функции координат и времени – волновой функции y (пси-функции), определяющей поведение частицы. Конкретный вид y -функции (ее математическое выражение) определяется состоянием частицы, характером поля, в котором она движется. Физический смысл имеет не сама y -функция, а квадрат ее модуля, | y | ², который характеризует вероятность пребывания частицы в определенном месте пространства. Зная, как меняется пси-функция от точки к точке, можно судить о том, где вероятнее всего можно встретить частицу. Исходя из этого, частицу удобно представить как бы «размазанной» в определенной области пространства в виде своеобразного облака переменной плотности. В атомной физике пользуются понятием электронного облака, распределенного в атоме или молекуле. Плотность электронного облака является непосредственной мерой вероятности пребывания электрона в определенной точке.

Вид y -функции в каждом конкретном случае можно получить путем решения волнового уравнения Шредингера, которое связывает y -функцию с массой m микрочастицы, ее полной энергией Е и потенциальной энергией Е_p:

,

где

.

Данное уравнение не содержит в качестве параметра время, поэтому оно описывает стационарные состояния.

Приняв уравнение Шредингера как математическое выражение фундаментальных свойств микросистем, можно получить ряд замечательных следствий, адекватно отражающих объективно существующие закономерности. В частности, можно вывести правила квантования полной энергии замкнутой системы. Оказывается, что уравнение Шредингера имеет решение не при любых значениях полной энергии системы, а лишь при некоторых, называемых собственными значениями. Совокупность собственных значений энергии называется спектром.

Таким образом, идея квантованности энергетических состояний атома, которая у Бора была гениальной догадкой и формулировалась в качестве постулата, оказывается следствием уравнения Шредингера.

У частицы, заключенной в результате взаимодействия с другими частицами в ограниченный объем пространства, спектр собственных значений энергии дискретный. Докажем это на примере частицы, находящейся в потенциальной яме (так называется область пространства, где потенциальная энергия минимальна).

Рассмотрим самый простой случай – одномерное движение частицы в потенциальной яме. Если волновая функция зависит только от одной координаты x, то уравнение Шредингера примет вид:

.

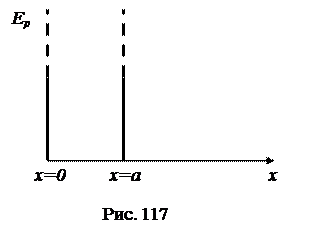
Пусть расстояние между стенками ямы равно а и стенки ямы бесконечно высокие: внутри ямы Е_p= 0, а за ее пределами Е_p= ∞ (рис. 117). В этом случае частица испытывает отражение от стенок, и попасть за пределы ямы не может. Пси-функция за пределами ямы и на ее границах равна нулю:

.

Так как внутри ямы Е_p= 0, то уравнение Шредингера в этом случае имеет вид:

.

Обозначив

,

получим уравнение, очень похожее на уравнение гармонического осциллятора:

.

Общее решение этого уравнения имеет вид:

,

в чем легко убедиться подстановкой.

Используя граничное условие y (0) = 0, получим 0 =В; следовательно,

.

Используя второе граничное условие y (а) = 0, получим

,

что возможно лишь в том случае, когда

,

где n – целое число, не равное нулю. Возведя обе части этого соотношения в квадрат и расписав k, получим:

,

где n= 1, 2, 3,…

Итак, в замкнутой системе стационарные состояния, т.е. состояния, в которых полная энергия со временем не меняется, возможны только при дискретных значениях полной энергии. В этом первое отличие квантовой картины мира от классической.

Второе отличие состоит в следующем. Если согласно классическим представлениям частица может с одинаковой вероятностью находиться в любой точке внутри потенциальной ямы, то согласно квантовой механике вероятность ее нахождения в разных точках различна. Эта вероятность определяется квадратом пси-функции. На рисунке 118, а изображен график функции y(x), а рисунке 118, б – график функции y²(x) для разных значений главного квантового числа n= 1, 2, 3. Как видно, вероятность нахождения частицы внутри потенциальной ямы на разных расстояниях от ее стенок неодинакова. При n= 1 вероятность нахождения частицы в середине ямы максимальна, при n= 2 равна нулю. Таким образом, классическая и квантовая физика дают разные предсказания о локализации частицы в пространстве.

Для электрона в атоме отдельная волновая функция определяет орбиталь, характеризуя распределение электронной плотности вокруг ядра. Поэтому под орбиталью понимают область пространства, где вероятность пребывания электрона достаточно велика (~90 %). Каждому состоянию электрона в атоме соответствует своя орбиталь с характерными очертаниями и ориентацией. Так, в невозбужденном атоме водорода электронное облако – сферическое образование с размытой границей максимальной плотностью на расстоянии 0,053 нм от ядра, что соответствует радиусу первой боровской орбиты. Знать форму и ориентацию орбиталей важно для понимания характера химической связи. Теоретический расчет электронной плотности по остову молекулы является главной задачей квантовой химии.

Уравнение Шредингера является фундаментальным уравнением квантовой механики и имеет для нее такое же значение, как законы Ньютона для классической механики. Оно не выводится, а составляется на основе аналогии с уравнениями для волновых процессов иной природы. Решение уравнения Шредингера – сложная математическая задача; это уравнение в большинстве случаев решается лишь приближенно. Для атома водорода оно решается точно.

Квантовая теория при определенных условиях переходит в классическую. Действительно, при больших значениях главного квантового числа n энергия частицы увеличивается, однако скачок энергии между соседними энергетическими уровнями становится малым по сравнению с энергией, и ее квантование не заметно.

Квантовые числа

Состояние электрона в атоме определяется совокупностью четырех квантовых чисел.

Главное квантовое число n= 1, 2, 3, …, ∞ определяет энергию электрона, обусловленную его взаимодействием с ядром. Каждому значению n соответствует свой энергетический уровень. С ростом n квантованные значения энергии увеличиваются, растет размер электронного облака.

В классической физике момент импульса частицы, обращающейся вокруг некоторой оси, – это вектор, направленный вдоль оси вращения. Известен его модуль и три его проекции на оси координат. Иной результат дает квантовая механика.

Любая вращающаяся система в квантовой механике может быть охарактеризована одновременно только двумя параметрами момента импульса – его модулем и одной из трех проекций момента импульса на какую-либо координатную ось. Две другие проекции не могут быть определены. Это значит, что направление вектора момента импульса системы в квантовой механике оказывается неопределенным, но проекция вектора на одно из выбранных направлений в пространстве может быть найдена.

Модуль момента импульса любой системы принимает только дискретный ряд значений, определяемых формулой:

,

где l= 1, 2, 3, … называется орбитальным квантовым числом ( =h/2π).

Проекция L_z момента импульса на некоторое избранное в пространстве направление (например, на направление вектора индукции магнитного поля) также принимает дискретный ряд значений, определяемых уравнением:

,

где m – магнитное квантовое число, принимающее значения m= 0, ±1, ±2, …± l (всего значений 2l+ 1).

Так как проекция вектора не может быть больше его модуля, то из двух последних уравнений следует, что магнитное квантовое число m не может превышать орбитальное квантовое число l, т.е. |m|≤l.

Сравнение этих формул с уравнением

не позволяет обнаружить связи полной энергии системы с ее моментом импульса или проекцией момента импульса на одну из координатных осей. Отсутствие прямой связи полной энергии системы с ее моментом импульса – одна из замечательных особенностей микромира, обнаруженная квантовой механикой. Однако полная энергия и момент импульса системы не являются все же полностью независимыми. Квантовая механика налагает одно ограничение на момент импульса: для любой системы уравнение Шредингера имеет решения лишь для значений орбитального квантового числа, удовлетворяющих условию

,

где n – главное квантовое число. Итак, l= 0, 1, 2, 3, …, n- 1.

Спиновое квантовое число m_s определяет возможные ориентации спина – собственного момента импульса (и связанного с ним спинового магнитного момента) электрона. На основе опытов установлено, что таких ориентаций может быть две. Спиновое квантовое число m_s может принимать два полуцелых значения ± 1/2, а проекция спина на выбранное направление – значения ±1/2 . В принятом выражении «спин ±1/2» речь идет не о самом спине, а о его проекции ±1/2 , т.е. в единицах .

Четыре квантовых числа n, l, m и m_s достаточны для полной характеристики электрона в атоме. По принципу Паули в атоме не может быть двух электронов с одинаковым набором квантовых чисел. Значит, на одной орбитали (с определенными значениями n, l, m) может находиться не более двух электронов с противоположными спинами. Одиночный (неспаренный) электрон на орбитали имеет нескомпенсированные спин и спиновой магнитный момент. Совокупность электронов с одинаковыми значениями n и l образует подслой. Так как m принимает не более 2l+1 значений, а m_s – не более двух, то число электронов в подслое не превышает 2(2 l+ 1 ). При заданном n число l принимает значения от 0 до n- 1, поэтому максимальное количество электронов в каждом слое можно найти, вычислив сумму

.

В заполненных слоях и подслоях спины электронов (как и спиновые магнитные моменты) попарно компенсируются, и значения полного спина и спинового магнитного момента равны нулю.

В атоме может существовать несколько электронных состояний с одинаковой энергией (вырожденные состояния). Вырождение исчезает при воздействии на атом магнитного и электрического полей. В состояниях с одним и тем же n, но разными l, m и m_s электроны по-разному взаимодействуют с внешними полями, и значения энергии, соответствующие этим состояниям, становятся разными.

Распределение электронов в атоме подчиняется принципу Паули и принципу минимума энергии (электрон занимает состояние с наименьшей энергией). Энергия электронных состояний в основном определяется квантовыми числами n и l. Переход атома из одного квантового состояния в другое сопровождается изменением квантовых чисел и перестройкой его электронного облака.

Глава 12

ФИЗИКА АТОМНОГО ЯДРА. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ

Date: 2016-11-17; view: 412; Нарушение авторских прав