Волны де Бройля. Соотношение неопределенностей

В 1924 г. Луи де Броль высказал гипотезу о том, что сочетание волновых и корпускулярных свойств является общим свойством любых материальных объектов, а не только света.

Это значит, что любое тело массой m, движущееся со скоростью u, может быть охарактеризовано длиной волны l и частотой n. По предположению де Бройля в нерелятивистском приближении (u<<c):

.

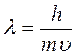Волновые свойства электронов были экспериментально обнаружены в опытах по дифракции электронов на кристаллах в 1927 г. Вид рассеянного пучка электронов такой же, как если бы падало электромагнитное излучение. В настоящее время обнаружены волновые свойства у других элементарных частиц, а также атомов и молекул.

Волновыми свойствами, согласно представлениям де Бройля, должны обладать любые материальные объекты. Но почему же эти свойства не обнаруживаются в опытах с макроскопическими телами? Для ответа на этот вопрос вычислим, например, дебройлевскую длину волны тела массой 1 г, движущегося со скоростью 0,5 м/с:

.

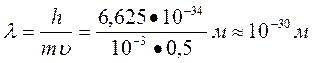Значение длины волны получилось на 20 порядков меньше размеров атома. Волновые эффекты такой малости невозможно обнаружить.

Таким образом, имеет место корпускулярно-волновая двойственность свойств частиц. Идея корпускулярно-волнового дуализма заключается не в механическом соединении двух взаимоисключающих моделей, а в признании такой сложности свойств микрообъектов, для полного описания которых не пригодны одни корпускулярные или только одни волновые представления. Описание свойств микрообъектов с использованием представлений о локализованных в пространстве частицах или о непрерывных волнах является упрощением реальности.

Обнаружение волновых свойств частиц привело к открытию фундаментального закона, управляющего всеми явлениями мира микрочастиц, – соотношения неопределенностей. Оно было открыто в 1927 г. В.Гейзенбергом. Согласно этому соотношению положение (координаты) и импульс (или скорость) движущейся частицы могут быть заданы одновременно лишь с ограниченной степенью точности, т.е. имеют некоторую неопределенность. Произведение неопределенности координаты Dx частицы на неопределенность проекции импульса Dp_x на данное направление не может быть меньше постоянной Планка:

.

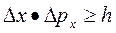Чем точнее определен импульс частицы, тем более неопределенной является ее координата. Учитывая связь между импульсом и энергией, можно получить соотношение неопределенности для энергии Е и времени t:

,

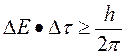где DЕ – неопределенность энергии некоторого состояния системы и Dt – время его существования. Чем больше время жизни системы, тем точнее определена ее энергия. Например, строго определенная энергия (DЕ→0) соответствует только основному состоянию атома, в котором он может пребывать как угодно долго (Dt→∞). В состоянии с малым временем жизни неопределенность в энергии достаточно велика и соответствующий энергетический уровень «размыт», что приводит к неопределенности в частоте спектральных линий. Наблюдаемые на опыте спектральные линии имеют поэтому конечную (естественную) ширину.

Соотношение неопределенности – прямое следствие волновых свойств микрочастиц. Отражая своеобразие микромира, оно свидетельствует о том, что возможности описания поведения микрочастиц с помощью понятий классической физики ограничены. В квантовой механике представление о точных значениях координаты, мгновенной скорости микрочастицы и определяемой ими траектории (в классическом понимании) теряет смысл. Законы сохранения импульса, энергии в квантовой механике выполняются строго.

Date: 2016-11-17; view: 689; Нарушение авторских прав