Теорема Ляпунова (центральна гранична теорема)

Теорема. Якщо випадкова величина Х може розглядатись як сума великого числа взаємно незалежних випадкових величин, вплив кожної з яких на всю суму нескінченно малий, то закон розподілу цієї випадкової величини Х, близький до нормального (з математичним сподіванням рівним 0), незалежно від того, які закони розподілу окремих доданків.

Тема: НАЙВАЖЛИВІШІ ЗАКОНИ РОЗПОДІЛУ ЙМОВІРНОСТЕЙ

1. Біноміальний закон розподілу

Імовірності в цьому законі визначаються за формулою m = 0,1,2, …, n. Закон справджується для схеми незалежних повторних випробувань, у кожному з яких подія А настає з імовірністю р. Частота настання події А має біноміальний закон розподілу. Числові характеристики розподілу:

2. Закон розподілу Пуассона

Дискретна випадкова величина має розподіл Пуассона, якщо вона набуває зліченної множини значень з імовірностями Цей розподіл описує кількість подій, які настають в однакові проміжки часу за умови, що ці події відбуваються незалежно одна від одної зі сталою інтенсивністю. Математичне сподівання і дисперсія в цьому розподілі однакові і дорівнюють а.

3. Геометричний розподіл

Закон подається формулою:

Геометричний закон розподілу має частота настання події у схемі незалежних повторних випробувань, якщо вони проводяться до першого настання події. У формулі р — імовірність настання події в кожному випробуванні. Числові характеристики розподілу:

4. Гіпергеометричний розподіл

Гіпергеометричний розподіл описує ймовірність настання m успішних результатів у n випробуваннях, якщо значення n мале порівняно з обсягом сукупності N:

Hаприклад, імовірність того, що з n деталей, які випадково вибрано з партії обсягом N, m виявляться дефектними, має гіпергеометричний закон розподілу (k — кількість дефектних деталей у партії). Числові характеристики розподілу:

5. Рівномірний закон розподілу

Якщо ймовірність потрапляння випадкової величини на інтервал пропорційна до довжини інтервалу і не залежить від розташування інтервалу на осі, то вона має рівномірний закон розподілу. Щільність такого розподілу:

Числові характеристики розподілу:

6. Показниковий закон розподілу

Щільність розподілу випадкової величини, розподіленої за показниковим законом, задається формулою: Числові характеристики: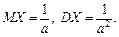

7. Нормальний закон розподілу

Нормальний закон розподілу задається щільністю Параметри , які входять до виразу щільності розподілу, є відповідно математичним сподіванням та середнім квадратичним відхиленням випадкової величини. Нормальний закон розподілу широко застосовується в математичній статистиці. Для обчислення ймовірності потрапляння випадкової величини, розподіленої нормально, на проміжок використовується функція Лапласа:

Ймовірність попадання нормально розподіленої випадкової величини на інтервал (a; b) дорівнює P(a<X<b)=F(b) -F(a).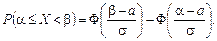

Часто застосовується також формула:

Date: 2016-11-17; view: 368; Нарушение авторских прав