Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Закон великих чисел. Центральна гранична теорема
|
|
Закон великих чисел можна загалом сформулювати так: у разі великого числа експериментів, що здійснюються для вивчення певної випадкової події або випадкової величини, середній їх результат практично перестає бути випадковим і може передбачатися з великою надійністю.
Закон великих чисел об’єднує кілька теорем (граничних теорем), у кожній з яких за певних умов виявляється факт наближення середніх характеристик під час проведення великої кількості експериментів до певних невипадкових, сталих величин. Граничні теореми встановлюють відповідність між теоретичними та дослідними характеристиками випадкових величин або випадкових подій при великій кількості випробувань.
Граничні теореми, які встановлюють граничні закони розподілу випадкових величин, об’єднують загальною назвою – центральна гранична теорема.
2. Нерівність Чебишова
Перша форма: якщо випадкова величина Х невід’ємна і має скінчене математичне сподівання: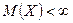 
, 
, то 
- нерівність Маркова
Друга форма: Якщо випадкова величина Х має обмежені М (Х); D (Х), то для довільного e > 0 має місце нерівність: 
або 
Читають: Ймовірність того, що модуль відхилення величини Х від свого математичного сподівання не перевищуватиме 
, більше або рівне за величину: 
(різницю між одиницею і відношенням дисперсії цієї величини до 
)
Теорема Чебишова
Нехай задано n незалежних випадкових величин X 1, X 2, … Xn, які мають обмежені математичні сподівання M (Хі) = 
(і = 1,…, n) і дисперсії яких D (Хі) не перевищують деякої сталої С (С > 0), тобто D (Хі) £ C.
Тоді для будь-якого малого додатного числа e імовірність відхилення середнього арифметичного цих величин 
від середнього арифметичного їх математичних сподівань 
, взятого за абсолютним значенням на величину e, буде як завгодно близькою до одиниці, якщо число випробувань n достатньо
велике, тобто 
, де
.
Отже, 
.
4. Теорема Бернуллі
Якщо ймовірність появи випадкової події А в кожному з n незалежних експериментів є величиною сталою і дорівнює р, то при необмеженому збільшенні числа експериментів n ® ¥ імовірність відхилення відносної частоти появи випадкової події W (A) від імовірності р, взятого за абсолютним значенням на величину e (e > 0) прямуватиме до одиниці зі зростанням n:
, де W (A) 
. Отже, 
Date: 2016-11-17; view: 369; Нарушение авторских прав