
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определений усилий в статически определимой балке с использованием численных методов
|
|
Цель задания: Рассчитать балку аналитически и методом конечных элементов. Проверить результаты ручного счета в ПК Scad.
Дана балка пролетом 6 м, на нее действует вертикальная распределенная нагрузка q.
Расчет балки аналитическим методом [17]:

Рисунок 3.106 – Эпюры
Решение:
Нахождение реакции опор:
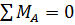 RB*l-q*l2/2=0
RB*l-q*l2/2=0

 -RA*l+q*l2/2=0
-RA*l+q*l2/2=0

Проверка правильности определения опорных реакций:
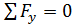 RA- q*l+R B =0
RA- q*l+R B =0
60-20*6+60=0 0≡0
1. Расчет эпюры поперечных сил Q:
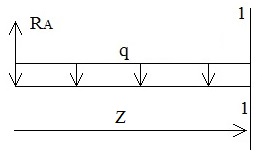

При z=0 Q=60 кН
При z=6 Q=60-20*6=-60 кН
2. Расчет изгибающих моментов:

При z=0 М=0 кН*м
При z=0 М=60*6-20*62/2=0 кН*м
 60=20*l l=3 метра
60=20*l l=3 метра
При z=3 М=60*3-20*32/2=90 кН*м
Расчет балки Методом Конечных Элементов с учётом равномерно распределённой нагрузки (анилитически) [23]:
В случаях, когда требуется учесть распределённую поперечную нагрузку, действующую вдоль оси стержня, необходимо заменить её статически эквивалентной системой сосредоточенных в узлах поперечных сил и изгибающих моментов. Заменим распределённую нагрузку постоянной интенсивности q, действующую по всей длине балочного элемента (Рисунок 3.108 а), статически эквивалентной системой сосредоточенных сил и моментов, приложенных в узлах элемента (Рисунок 3.108 б).
Рисунок 3.108 – Учёт равномерно распределённой нагрузки
Перерезывающее усилие, действующее на элементарном участке dх:
dF = qdx.
Элементарная работа перерезывающей силы на перемещении v(х):
δW = v (x)・ dF = v (x)・ qdx = Фu qdx.
Работа распределённой нагрузки

Работа эквивалентной системы нагружения (рисунок 3.10 б)
W= Fiνi+Miθi+Fjνj+Mjθj=FTu={Fi Mi Fj Mj}u
Сравнивая уравнения, получим (Рисунок 3.108 в) 


Рисунок 3.109 – Схема балки
Уравнение для определения неизвестных реакций:
 (1)
(1)
Геометрические характеристики сечения:
– площадь: А=b*h=0.4*0.7=028 м2;
– момент инерции: Ix=b*h3/12=2.133*10-3;
Заменим нагрузку q статически эквивалентной системой сил и моментов. Силовые граничные условия:

Формируем матрицу жесткости конечного элемента. Так как каждый узел имеет две степени свободы, а узлов 2, то размерность матрицы жесткости конструкции 4х4.


Кинематические 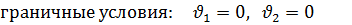
Уравнение равновесия системы с учётом граничных условий:
 (2)
(2)


Уравнение для нахождения неизвестных перемещений:


Откуда находим:


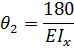

Подставляем значения  и
и  в уравнение (1):
в уравнение (1):


 Расчет балки МКЭ в ПК SCAD:
Расчет балки МКЭ в ПК SCAD:
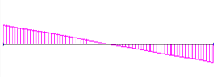 Рисунок 3.109 – Расчетная схема балки в SCAD
Рисунок 3.109 – Расчетная схема балки в SCAD
Рисунок 3.110 – Эпюра изгибающих моментов

Рисунок 3.111 – Эпюра продольных усили
Вывод расчета: Расхождение результатов расчета в пределах 5%.
| Изм. |
| Кол.уч |
| Лист № док. |
| Подп. |
| Дата |
| Лист |
| Д.340.0.015.08.ПЗ |
| Разраб. |
| Янгутова Е.Г. |
| Проверил |
| Бохоева Л.А |
| Консульт. . |
| Жаркая Г.Ф. |
| Н.контр. |
| Бундаев В.В. |
| Утвердил |
| Бохоева Л.А. |
| Моделирование и расчёт строительных конструкций административного здания |
| Стадия |
| Листов |
| 134 |
| ВСГУТУ, гр. 370-1 |
ЭКОНОМИЧЕСКАЯ ЧАСТЬ
4. ЭКОНОМИЧЕСКАЯ ЧАСТЬ.
Date: 2016-06-06; view: 2539; Нарушение авторских прав